大白话讲梯度下降-含举例【入门级】

用最简单的语言和例子来解释梯度下降和反向传播，帮助你理解这个过程。

---

1. 梯度下降是干什么的？

梯度下降是一种优化算法，它的目标是找到一个函数的最小值。在机器学习中，这个“函数”通常是损失函数（Loss Function），它衡量模型的预测结果和真实结果之间的差距。

• 目标：通过调整模型的参数（比如权重），让损失函数的值越来越小，最终让模型的预测更准确。

---

2. 梯度是什么？

梯度是一个数学概念，表示函数在某一点的变化率（或者说斜率）。在梯度下降中，梯度告诉我们：

• 损失函数在当前参数下，是上升还是下降。
• 如果梯度是正的，说明损失函数在增加；如果梯度是负的，说明损失函数在减少。

---

3. 梯度下降的过程

梯度下降的核心思想是：沿着梯度的反方向调整参数，因为这样可以减少损失函数的值。

举个例子：

假设你在山上，目标是找到山谷的最低点（即损失函数的最小值）。你每次只能走一小步，怎么走才能最快到达山谷呢？

1. 观察坡度：看看你脚下的坡度是向上还是向下。
2. 决定方向：如果坡度向上，你就往下走；如果坡度向下，你就继续往下走。
3. 迈出一步：根据坡度的大小，决定你这一步走多远（步长由学习率控制）。
4. 重复：不断重复这个过程，直到你走到最低点。

---

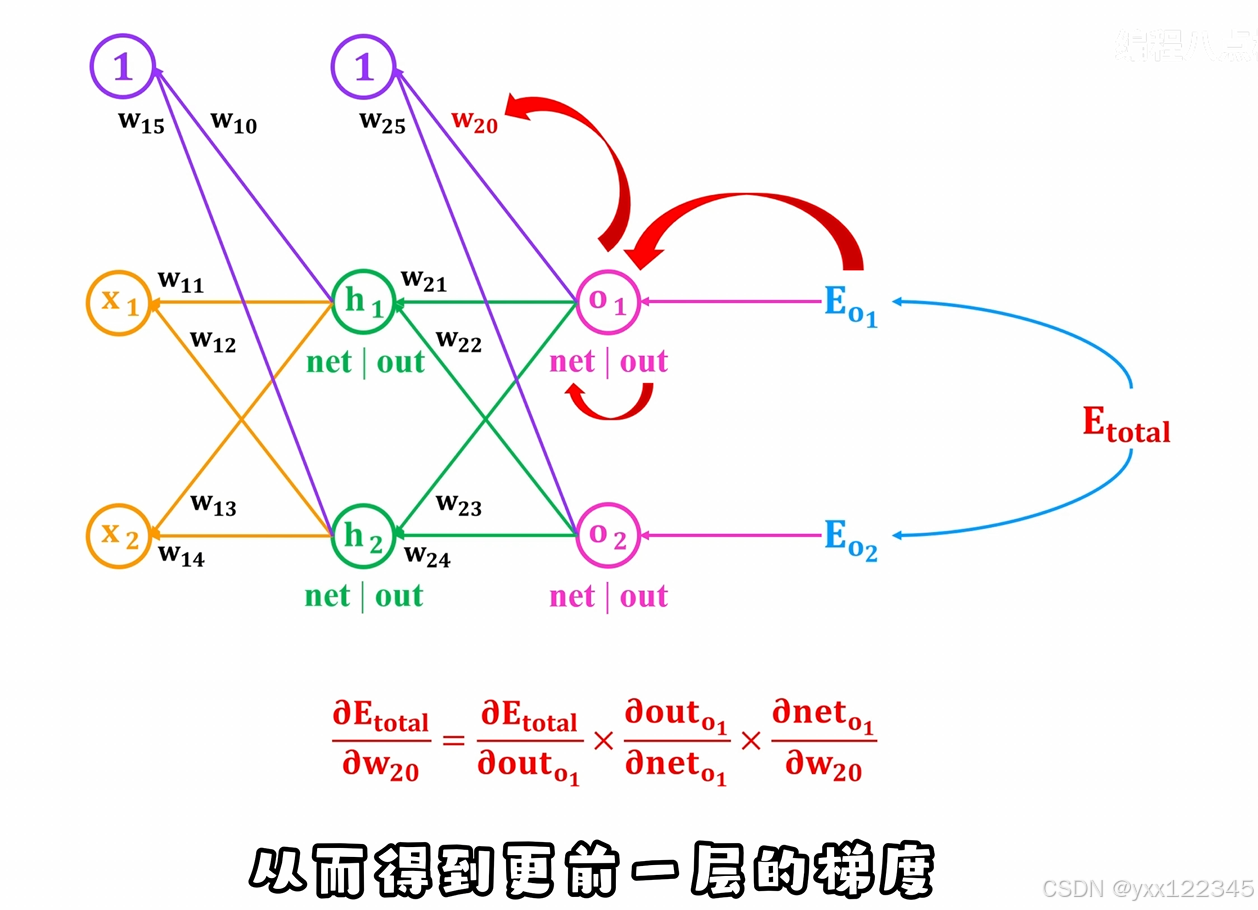
4. 反向传播的作用

反向传播是梯度下降的一个关键步骤，它的作用是计算梯度。

• 问题：在神经网络中，参数非常多（比如权重和偏置），如何高效地计算每个参数的梯度？
• 解决方法：反向传播通过链式法则，从输出层开始，逐层计算每个参数的梯度。

举个例子：

假设你有一个简单的神经网络：

1. 输入：输入数据。
2. 计算：数据经过每一层的计算，最终得到输出。
3. 比较：输出和真实值比较，计算损失。
4. 反向传播：
   • 从损失开始，逐层往回计算每个参数对损失的贡献（即梯度）。
   • 通过链式法则，将梯度从输出层传递到输入层。

---

5. 梯度下降的步骤总结

1. 初始化参数：随机设置模型的参数（比如权重）。
2. 前向传播：用当前参数计算模型的输出。
3. 计算损失：比较输出和真实值，计算损失函数的值。
4. 反向传播：计算每个参数的梯度（即损失函数对参数的变化率）。
5. 更新参数：沿着梯度的反方向，调整参数。
   • 公式：新参数 = 旧参数 - 学习率 × 梯度
6. 重复：不断重复前向传播、计算损失、反向传播和更新参数，直到损失函数的值足够小。

---

6. 学习率的作用

学习率是一个超参数，控制每次参数更新的步长。

• 学习率太大：可能会导致跳过最小值，甚至无法收敛。
• 学习率太小：可能会导致收敛速度过慢。
• 合适的学习率：可以让模型快速且稳定地找到最小值。

---

7. 总结

• 梯度下降：通过不断调整参数，找到损失函数的最小值。
• 反向传播：高效计算每个参数的梯度。
• 学习率：控制参数更新的步长。

---

举例（包含梯度为正和负的情况）

假设你有一个简单的函数：y = (x - 3)^2，你想找到它的最小值（即 x = 3）。

情况 1：梯度为正（x > 3）

1. 初始化：设 x = 5。
2. 计算梯度：对 x 求导，梯度为 2(x - 3)。当 x = 5 时，梯度是 2(5 - 3) = 4（为正）。
3. 更新参数：假设学习率是 0.1，则新 x = 5 - 0.1 × 4 = 4.6。
4. 解释：因为梯度为正，说明 x 需要减小才能接近最小值。

情况 2：梯度为负（x < 3）

1. 初始化：设 x = 1。
2. 计算梯度：对 x 求导，梯度为 2(x - 3)。当 x = 1 时，梯度是 2(1 - 3) = -4（为负）。
3. 更新参数：假设学习率是 0.1，则新 x = 1 - 0.1 × (-4) = 1 + 0.4 = 1.4。
4. 解释：因为梯度为负，说明 x 需要增加才能接近最小值。

情况 3：梯度为零（x = 3）

1. 初始化：设 x = 3。
2. 计算梯度：对 x 求导，梯度为 2(x - 3)。当 x = 3 时，梯度是 2(3 - 3) = 0。
3. 更新参数：梯度为零，说明已经找到最小值，参数不再更新。

---

总结

• 梯度为正：参数需要减小。
• 梯度为负：参数需要增加。
• 梯度为零：达到最小值，停止更新。

通过这个例子，你可以看到梯度下降如何根据梯度的正负来调整参数，最终找到函数的最小值！ 😊