机器人运动学笔记1——林沛群

1 导论

新增部分：无伤理解欧拉角中的“万向死锁”现象

参考自视频：台大机器人学之运动学——林沛群
平面：2个移动DOF，1个转动DOF
空间：3个移动DOF，3个转动DOF

刚体运动状态描述，在刚体上建立刚体坐标系（一般在质心）:

• 移动：刚体的位置通过坐标轴原点来表示
• 转动：刚体的姿态通过刚体坐标轴相对于世界坐标轴之间的夹角来表示

记录运动轨迹，对轨迹进行微分，可以得到运动过程中的速度和加速度信息。

1.1 移动

移动：以向量P来描述{B}的原点相对于{A}的状态

1.2 转动

转动：描述{B}相对于{A}的姿态。——旋转矩阵

${}_B^{A}R$为B相对于A的旋转矩阵，${}^A{\hat{X}}_B$表示B刚体的x轴基向量相对于世界坐标系A的各个分量。即B的x轴在A的三轴上的投影分量。
例题：

答案：

1.3 旋转矩阵

• 特性1：${}_B^{A}R{=}_A^B{R}^T$即B相对于A的旋转矩阵等于A相对于B的旋转矩阵的转置。
• 特性2：${}_B^A{R}^T$${}_B^{A}R$= $\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$=$\mathrm{I}$，可得${}_B^A{R}^T{=}_B^A{R}^{-1}{=}_A^{B}R$，因此旋转矩阵是正交矩阵。旋转矩阵内三列两两垂直，又为单位正交基。行列式为1。

  由于是单位正交基，则有6个限制条件（3个(列的模为1)+3个两两垂直），但旋转矩阵有9个元素，因此旋转矩阵只有3个DOF，与空间中转动具有3个DOF符合。

旋转矩阵还可以用于转换向量的坐标：
  将在{B}坐标系中表示的向量P转换到在{A}坐标系中表示的向量P，${}^{A}P$=${}_B^{A}R$ ${}^{B}P$。

旋转矩阵还可以用于进一步描述物体转动的状态。
关于Z轴(逆时针为正)旋转的旋转矩阵为：
$$R_{{\hat{z}}_A(\theta )}=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}c\theta & -s\theta & 0\\ s\theta & c\theta & 0\\ 0& 0& 1\end{array}\right]$$
关于X轴(逆时针为正)旋转的旋转矩阵为：
$$R_{{\hat{x}}_A(\theta )}=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & -sin\theta \\ 0& sin\theta & cos\theta \end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& c\theta & -s\theta \\ 0& s\theta & c\theta \end{array}\right]$$
关于Y轴(逆时针为正)旋转的旋转矩阵为：
$$R_{{\hat{y}}_A(\theta )}=\left[\begin{array}{ccc}cos\theta & 0& sin\theta \\ 0& 1& 0\\ -sin\theta & 0& cos\theta \end{array}\right]=\left[\begin{array}{ccc}c\theta & 0& s\theta \\ 0& 1& 0\\ -s\theta & 0& c\theta \end{array}\right]$$

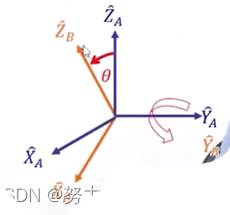
例题A投影到B：

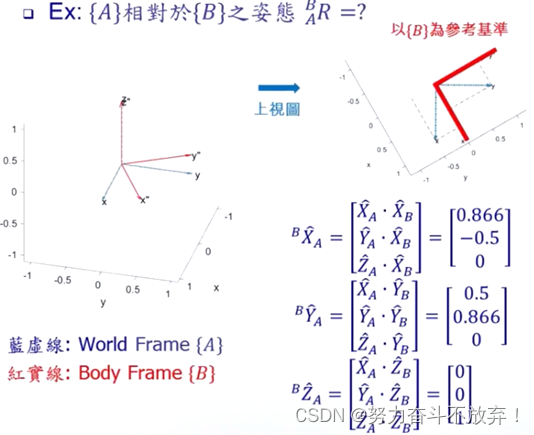
答案：

2 旋转矩阵与转角

  拆解成三次旋转连乘时要注意，旋转矩阵不支持交换律，因此需要明确多次旋转的先后顺序，旋转转轴也需要明确定义，是对固定不动的轴旋转还是对当下frame坐标轴的转轴做旋转。

由于上述原因将拆解方式分为两种：

1. 对方向固定不动得转轴旋转Fixed angles。
2. 对转动得frame当下所在的转轴方向旋转Euler angles。

2.1 Fixed Angles——正解

每次旋转都是对于不动的绿色坐标轴做旋转。
公式为：$${}_B^A{R}_{XYZ}(\gamma ,\beta ,\alpha )=R_Z(\alpha )R_Y(\beta )R_X(\gamma )=\left[\begin{array}{ccc}c\alpha & -s\alpha & 0\\ s\alpha & c\alpha & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}c\beta & 0& s\beta \\ 0& 1& 0\\ -s\beta & 0& c\beta \end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& c\gamma & -s\gamma \\ 0& s\gamma & c\gamma \end{array}\right]=\left[\begin{array}{ccc}c\alpha c\beta & c\alpha s\beta s\gamma -s\alpha c\gamma & c\alpha s\beta c\gamma +s\alpha s\gamma \\ s\alpha c\beta & s\alpha s\beta s\gamma +c\alpha c\gamma & s\alpha s\beta c\gamma -c\alpha s\gamma \\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{array}\right]$$
顺序是从开始到结束不断左乘旋转矩阵，即先转的放后面。
例题：

2.2 Fixed Angles——逆解

$${}_B^A{R}_{XYZ}(\gamma ,\beta ,\alpha )=\left[\begin{array}{ccc}c\alpha c\beta & c\alpha s\beta s\gamma -s\alpha c\gamma & c\alpha s\beta c\gamma +s\alpha s\gamma \\ s\alpha c\beta & s\alpha s\beta s\gamma +c\alpha c\gamma & s\alpha s\beta c\gamma -c\alpha s\gamma \\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{array}\right]=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$
If $\beta \ne 90°$，
 $\beta =Atan2(-r_{31},\sqrt{{r_{11}}^2+{r_{21}}^2})$
 $\alpha =Atan2(r_{21}/c\beta ,r_{11}/c\beta )$
 $\gamma =Atan2(r_{32}/c\beta ,r_{33}/c\beta )$

2.3 Euler Angles——Z-Y-X由angle推算R

每次旋转都是对于当下坐标系的轴做旋转。转轴先后为Z-Y-X。
公式是：$${}_B^A{R}_{Z^{\prime }{Y}^{\prime }{X}^{\prime }}(\alpha ,\beta ,\gamma )=R_{Z^{\prime }}(\alpha )R_{Y^{\prime }}(\beta )R_{X^{\prime }}(\gamma )$$
先转的放前面，结果与固定轴X-Y-Z旋转获得同样的结果。欧拉角先对Y转30°再对X转60°，等于固定角先对X转60°再对Y转30°。

2.4 Euler Angles——Z-Y-Z由angle推算R和R求解angle

Z-Y-Z公式为：$${}_B^A{R}_{Z^{\prime }{Y}^{\prime }{Z}^{\prime }}(\alpha ,\beta ,\gamma )=R_{Z^{\prime }}(\alpha )R_{Y^{\prime }}(\beta )R_{Z^{\prime }}(\gamma )$$
$${}_B^A{R}_{Z^{\prime }{Y}^{\prime }{Z}^{\prime }}(\alpha ,\beta ,\gamma )=\left[\begin{array}{ccc}c\alpha c\beta c\gamma -s\alpha s\gamma & -c\alpha c\beta s\gamma -s\alpha c\gamma & c\alpha s\beta \\ s\alpha c\beta c\gamma +c\alpha s\gamma & -s\alpha c\beta s\gamma +c\alpha c\gamma & s\alpha s\beta \\ -s\beta c\gamma & s\beta s\gamma & c\beta \end{array}\right]=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$
If $\beta \ne 0°$
 $\beta =Atan2(\sqrt{{r_{31}}^2+{r_{32}}^2},r_{33})$
 $\alpha =Atan2(r_{23}/s\beta ,r_{13}/s\beta )$
 $\gamma =Atan2(r_{32}/s\beta ,-r_{31}/s\beta )$

例题：

2.5 Fixed angles和Euler angles小结

两种方法达到某个姿态都有12种根据坐标轴转动三次的旋转方式(3X2X2)。
Angle-axis表达法：

Quaternion（四元数）表达法：

2.6 Mapping——齐次变换矩阵

将移动和转动整合到一起，完成两个参考系之间的映射。
齐次变换矩阵描述了一个参考系相对于另一个参考系的状态。
齐次变换矩阵(Homogeneous transformation matrix)：$${}_B^{A}T={\left[\begin{array}{cc}{}_B^A{R}_{3\times 3}& {}_{}^A{P}_{{Borg}_{3\times 1}}\\ \begin{array}{ccc}0& 0& 0\end{array}& 1\end{array}\right]}_{4\times 4}$$
示例向量P从B参考系转换到A参考系：


转换矩阵可以连乘来达到参考系的转换：${}_B^{A}T={}_C^{A}T{}_D^{C}T{}_B^{D}T$,从B参考系转换到A参考系，中间经过C和D参考系。

2.7 Operators——齐次变换矩阵

齐次变换矩阵做为运算子。对向量进行移动旋转操作。类似mapping，只不过mapping是将B参考系的向量映射到A参考系，而operator是将A参考系向量运算到与B参考系相同的向量下时，此时这个向量相对A参考系的坐标位置。
示例(先旋转再移动)：

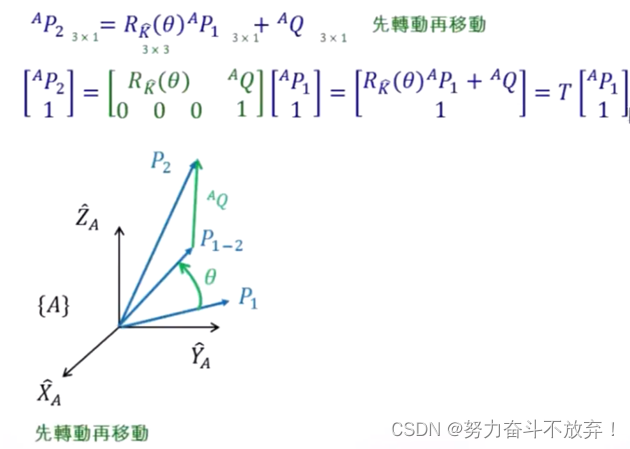
齐次变换矩阵做为运算子。对参考系进行与向量相反的移动旋转操作。即当看作是对向量做运算时，将向量向前移动，参考系不动，当看作对参考系做运算时，相当于将参考系向后移，向量不动。


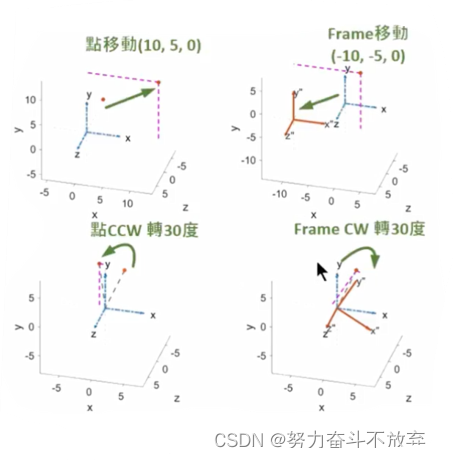
示例：

2.8 Transformation Matrix

连续运算$${}_{}^{A}P={}_B^{A}T{}_{}^{B}P={}_B^{A}T{}_C^{B}T{}_{}^{C}P=\left[\begin{array}{cc}{}_B^{A}R{}_C^{B}R& {}_{}^A{P}_{Borg}+{}_B^{A}R{}_{}^B{P}_{Corg}\\ \begin{array}{ccc}0& 0& 0\end{array}& 1\end{array}\right]={}_C^{A}T{}_{}^{C}P$$将C参考系种的向量转换到A坐标系

齐次矩阵的逆矩阵：$${}_B^{A}T={\left[\begin{array}{cc}{}_B^A{R}_{3\times 3}& {}_{}^A{P}_{{Borg}_{3\times 1}}\\ \begin{array}{ccc}0& 0& 0\end{array}& 1\end{array}\right]}_{4\times 4}$$
$${}_B^A{T}^{-1}={}_A^{B}T=\left[\begin{array}{cc}{}_B^A{R}^T& -{}_B^A{R}^T{}_{}^A{P}_{Borg}\\ \begin{array}{ccc}0& 0& 0\end{array}& 1\end{array}\right]$$
向量变换过程中的左乘和右乘：

1. operator角度：某一个在{A}的向量，经过与{B}相同的变换，与{B}中向量重合。左乘
2. mapping角度：某一个在{B}参考系中的向量，经过变换后，以{A}参考系表达该向量。右乘

以固定的{A}或者移动的{B}为基准做移动旋转操作，变换矩阵应该用不同的连乘方式。

---

总结

本文主要包含了基础性的矩阵内容笔记，为接下来是正、逆运动学部分做准备，下一篇是正、逆运动学部分内容笔记。