一个多位加法器可以由多个一位加法器拼接而成,其加法器的逻辑表达式为:
由这个表达式可以得出一个简单的电路就是ripple adder,将前一级的进位输出放到后一级的进位输入上这样多个全加器串联起来就可以得到一个多位加法器。然而这样简单的电路对于现今的计算机速度发展趋势并不符合要求,前一级从输入到输出会产生一个延迟,而如果全加器添得太多,高位的延迟就会累加到甚至肉眼可见。存在这个问题的关键原因是进位的不能同时产生,如果说进位可以同时产生那么高位就不需要花时间等待所有低位进位产生了。
首先明确需要在carry上改动那么就需要在下面的上进行理解上的升华
这个式子可以划分为两部分
——这一部分可以看作本位是否产生进位,当两个输入都为1时这个式子结果就是1,因此这一部分称为generate
——这一部分可以看作是对前一位进位的传播,因为当两个输入其中一个为1时另一个为0,则表示本位并没有产生进位,唯一影响整个
就只有前一位为进位而已。为了迎合S中的符号,并在逻辑电路中更好表达,一般而言会将这里的
改为
。由真值表可知这样的改变并不会影响整个表达式的逻辑。这一部分称为propagate
由此可得:
也就是说:
……
如果说将的表达式代入
中,那么就可得到
仅关于
的表达式,以此类推就可以得到之后所有位的表达式
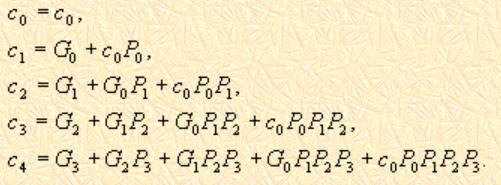
将其转化为逻辑电路,就可以得到我们所需要的carry look-ahead adder(CLA),其所有的进位都是同时生成,只要输入可用,可用就可以出结果了。其电路结构如下所示

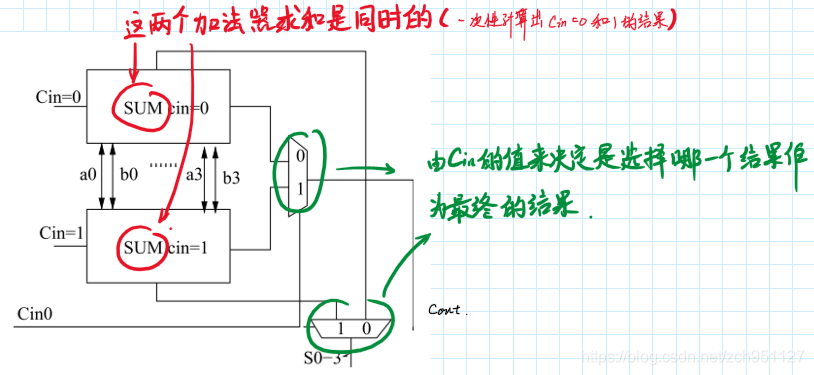
除此之外减少延迟的方法还有carry select adder,其设计理念就是事先将carry可能出现的两种结果作为输入算出来,然后等到真实的carry可用时便可以直接通过multiplexer选择需要的结果。这个在处理位数较高的计算时比较合适,其可以将所有的位划分成好几个组,每个组用一个这个玩意,这样所需要的延迟也就是前一组carry的延迟而已了,其结构如下图所示
第三种方式是Parallel Tree/Perfix adder,这算是一整类adder因为其结构可以自由设计,这一类的加法器市面上的主要有下面几种
Ladner-Fischer adder, Kogge-Stone adder, Brent-Kung adder, Han-Carlson adder
这里主要介绍Ladner-Fischer adder,这也是之前有提到过的Pentium4使用的解决方案,其在所有的此类加法器中逻辑深度是最浅的,这意味着其运算速度是最快的。其余的方式也就是拓扑结构不一样,其原理都是同样的。
这一类加法器运行过程主要有三个阶段:
1. Pre-processing stage 这个阶段生成每每一对输入的和
2. Carry generation network 这一阶段每一个bit加法器的进位所需要的和
(其每一行生成进位的进度是同时的)
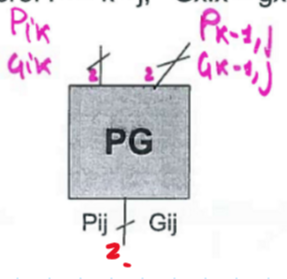
3. Post processing stage这个阶段中做的就是将生成的和
组合成需要的结果即
和
最终的结构入下图所示






















 623
623

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








