机器学习时间序列模型：隐马尔可夫模型HMM（3）

一、HMM模型的学习问题(Baum-Welch算法)

(1) Baum-Welch算法介绍

HMM的学习算法Baum-Welch（也称为EM算法）是一种无监督学习算法，用于从观测序列中估计HMM模型的参数，包括初始概率向量、状态转移概率矩阵和观测概率矩阵。

Baum-Welch算法的主要步骤如下：

【1】初始化：随机初始化HMM模型的参数，包括初始概率向量、状态转移概率矩阵和发射概率矩阵（即观测矩阵B）。

【2】E步骤（Expectation）：对于每个观测序列，使用前向-后向算法计算前向概率矩阵alpha和后向概率矩阵beta。

【3】M步骤（Maximization）：利用E步骤中计算得到的前向概率矩阵alpha、后向概率矩阵beta以及观测序列，更新HMM模型的参数。

   - 更新初始概率向量pi：根据alpha和beta计算得到的gamma矩阵。

   - 更新状态转移概率矩阵A：根据alpha、beta和观测序列计算得到的xi矩阵。

   - 更新发射概率矩阵B：根据alpha、beta和观测序列计算得到的gamma矩阵。

【4】重复步骤2和3，直到收敛或达到最大迭代次数。

在E步骤中，利用前向-后向算法计算前向概率矩阵alpha和后向概率矩阵beta。前向概率alpha表示在给定模型参数和观测序列的条件下，到达每个时间步和隐藏状态的路径的概率。后向概率beta表示在给定模型参数和观测序列的条件下，从每个时间步和隐藏状态出发，到达观测序列结束的路径的概率。

在M步骤中，根据E步骤中计算得到的前向概率矩阵alpha、后向概率矩阵beta以及观测序列，利用各种计算公式更新HMM模型的参数。通过不断迭代E步骤和M步骤，逐渐优化模型参数，使得模型能够更好地解释观测序列。

Baum-Welch算法是一种经典的HMM学习算法，它利用了观测序列中的信息来估计模型参数，从而提高了HMM模型的拟合能力。然而，Baum-Welch算法可能会陷入局部最优解，并且对于有多个局部最优解的情况，无法保证找到全局最优解。因此，在实际应用中，可能需要多次运行Baum-Welch算法以选择最优的模型参数。

(2) Baum-Welch算法推导过程介绍

为了让有基础的读者进一步了解Baum-Welch算法，为了他们的学术研究乃至创新需要，笔者给大家查找了该算法推导过程的资料，以方便读者参考。

输入：给定训练数据只包含观测序列，而没有对应的状态序列

输出：学习HMM模型λ = (π, A, B)的参数

学习方法：参数的学习可以由EM算法来实现

步骤-1：确定对数似然函数

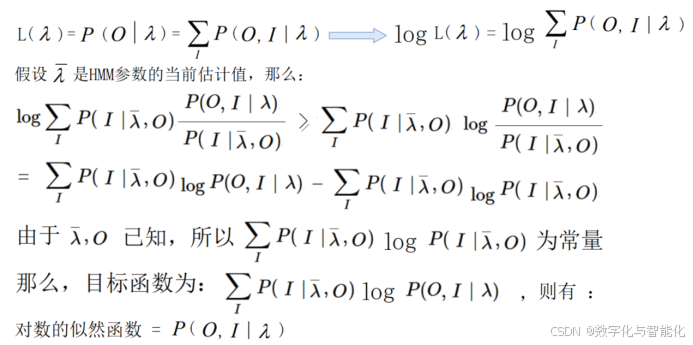
步骤-2：EM算法的E步

步骤-3：EM算法的M步

步骤4：求初始概率向量π

步骤-5：求状态转移矩阵A

步骤-6：求观测概率分布矩阵B

(3) Baum-Welch算法案例-天气预测

我们以天气预报案例为例，假设有三种天气状态：晴天（Sunny）、多云（Cloudy）和雨天（Rainy），以及两种观测结果：干燥（Dry）和湿润（Wet）。我们收集了7天的天气数据，如下所示：

天气状态：Sunny, Sunny, Cloudy, Rainy, Rainy, Cloudy, Sunny

观测结果：Dry, Wet, Wet, Dry, Wet, Wet, Dry

注释：S表示晴天，C表示多云，R表示雨天；D表示干燥，W表示湿润。

代码实现：

import numpy as np

def baum_welch(obs, n_states, n_obs):

    # 初始化参数

    start_prob = np.ones(n_states) / n_states  # 初始状态