Random Forest(s),随机森林,又叫Random Trees[2][3],是一种由多棵决策树组合而成的联合预测模型,天然可以作为快速且有效的多类分类模型。如下图所示,RF中的每一棵决策树由众多split和node组成:split通过输入的test取值指引输出的走向(左或右);node为叶节点,决定单棵决策树的最终输出,在分类问题中为类属的概率分布或最大概率类属,在回归问题中为函数取值。整个RT的输出由众多决策树共同决定,argmax或者avg。
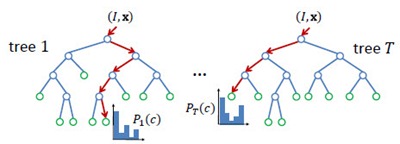
Node Test
node test通常很简单,但很多简单的拧在一起就变得无比强大,联合预测模型就是这样的东西。node test是因应用而异的。比如[1]的应用是基于深度图的人体部位识别,使用的node test是基于像素x的深度比较测试:
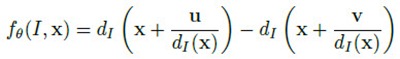
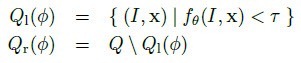
简单的说,就是比较像素x在u和v位移上的像素点的深度差是否大于某一阈值。u和v位移除以x深度值是为了让深度差与x本身的深度无关,与人体离相机的距离无关。这种node test乍一看是没有意义的,事实上也是没多少意义的,单个test的分类结果可能也只是比随机分类好那么一丁点。但就像Haar特征这种极弱的特征一样,起作用的关键在于后续的Boosting或Bagging——有效的联合可以联合的力量。
Training
RF属于Bagging类模型,因此大体训练过程和Bagging类似,关键在于样本的随机选取避免模型的overfitting问题。RF中的每棵决策树是分开训练的,彼此之间并无关联。对于每棵决策树,训练之前形成一个样本子集,在这个子集中有些样本可能出现多次,而另一些可能一次都没出现。接下去,就是循序决策树训练算法的,针对这个样本子集的单棵决策树训练。
单棵决策树的生成大致遵循以下过程:
1)随机生成样本子集;
2)分裂当前节点为左右节点,比较所有可选分裂,选取最优者;
3)重复2)直至达到最大节点深度,或当前节点分类精度达到要求。
这一过程是贪婪的。
当然对于不同的应用场合,训练过程中,会有细节上的差别,比如样本子集的生成过程、以及最优分割的定义。
在[1]中,决策树的真实样本其实是图片中的像素x,变量值则是上文提到的node test。但是,对于一张固定大小的图片而言可取的像素x是可数大量的,可取的位移(u,v)和深度差阈值几乎是不可数无限的。因此,[1]在训练单棵决策树前,要做的样本子集随机其实涉及到像素x集合的随机生成、位移(u,v)和深度差阈值组合的随机生成,最后还有训练深度图集合本身的随机生成。
最优分裂通常定义为使信息增量最大的分类,如[1]中的定义:
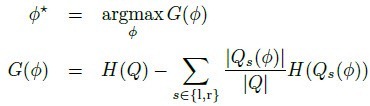
H指熵,通过分裂子集的部位标签分布计算。
Reference:
[1] J. Shotton, A. Fitzgibbon, M. Cook, T. Sharp, M. Finocchio, R. Moore, A. Kipman, and A. Blake. Real-Time Human Pose Recognition in Parts from a Single Depth Image . In CVPR 2011.
[2] L. Breiman. Random forests . Mach. Learning, 45(1):5–32, 2001.
[3] T. Hastie, R. Tibshirani, J. H. Friedman. The Elements of Statistical Learning . ISBN-13 978-0387952840, 2003, Springer.
[4] V. Lepetit, P. Lagger, and P. Fua. Randomized trees for real-time keypoint recognition . In Proc. CVPR, pages 2:775–781, 2005.
在OpenCV1.0\ml\include\ml.h文件中,定义了机器学习的多种模型和算法的结构文件,现将有关决策树和随机森林的定义罗列如下:
结构体struct:
CvPair32s32f;
CvDTreeSplit;
CvDTreeNode;
CvDTreeParams;
CvDTreeTrainData;
CvRTParams;
类class:
CvDTree: public CvStatModel
CvForestTree: public CvDTree
CvRTrees: public CvStatModel
OpenCV2.3中Random Trees(R.T.)的继承结构:

API:
| CvRTParams | 定义R.T.训练用参数,CvDTreeParams的扩展子类,但并不用到CvDTreeParams(单一决策树)所需的所有参数。比如说,R.T.通常不需要剪枝,因此剪枝参数就不被用到。 max_depth 单棵树所可能达到的最大深度 min_sample_count 树节点持续分裂的最小样本数量,也就是说,小于这个数节点就不持续分裂,变成叶子了 regression_accuracy 回归树的终止条件,如果所有节点的精度都达到要求就停止 use_surrogates 是否使用代理分裂。通常都是false,在有缺损数据或计算变量重要性的场合为true,比如,变量是色彩,而图片中有一部分区域因为光照是全黑的 max_categories 将所有可能取值聚类到有限类,以保证计算速度。树会以次优分裂(suboptimal split)的形式生长。只对2种取值以上的树有意义 priors 优先级设置,设定某些你尤其关心的类或值,使训练过程更关注它们的分类或回归精度。通常不设置 calc_var_importance 设置是否需要获取变量的重要值,一般设置true nactive_vars 树的每个节点随机选择变量的数量,根据这些变量寻找最佳分裂。如果设置0值,则自动取变量总和的平方根 max_num_of_trees_in_the_forest R.T.中可能存在的树的最大数量 forest_accuracy 准确率(作为终止条件) termcrit_type 终止条件设置 — CV_TERMCRIT_ITER 以树的数目为终止条件,max_num_of_trees_in_the_forest生效 – CV_TERMCRIT_EPS 以准确率为终止条件,forest_accuracy生效 — CV_TERMCRIT_ITER | CV_TERMCRIT_EPS 两者同时作为终止条件 |
| CvRTrees::train | 训练R.T. return bool 训练是否成功 train_data 训练数据:样本(一个样本由固定数量的多个变量定义),以Mat的形式存储,以列或行排列,必须是CV_32FC1格式 tflag trainData的排列结构 — CV_ROW_SAMPLE 行排列 — CV_COL_SAMPLE 列排列 responses 训练数据:样本的值(输出),以一维Mat的形式存储,对应trainData,必须是CV_32FC1或CV_32SC1格式。对于分类问题,responses是类标签;对于回归问题,responses是需要逼近的函数取值 var_idx 定义感兴趣的变量,变量中的某些,传null表示全部 sample_idx 定义感兴趣的样本,样本中的某些,传null表示全部 var_type 定义responses的类型 — CV_VAR_CATEGORICAL 分类标签 — CV_VAR_ORDERED(CV_VAR_NUMERICAL)数值,用于回归问题 missing_mask 定义缺失数据,和train_data一样大的8位Mat params CvRTParams定义的训练参数 |
| CvRTrees::train | 训练R.T.(简短版的train函数) return bool 训练是否成功 data 训练数据:CvMLData格式,可从外部.csv格式的文件读入,内部以Mat形式存储,也是类似的value / responses / missing mask。 params CvRTParams定义的训练参数 |
| CvRTrees:predict | 对一组输入样本进行预测(分类或回归) return double 预测结果 sample 输入样本,格式同CvRTrees::train的train_data missing_mask 定义缺失数据 |
Example:
- #include <cv.h>
- #include <stdio.h>
- #include <highgui.h>
- #include <ml.h>
- #include <map>
- void print_result(float train_err, float test_err,
- const CvMat* _var_imp)
- {
- printf( "train error %f\n", train_err );
- printf( "test error %f\n\n", test_err );
- if (_var_imp)
- {
- cv::Mat var_imp(_var_imp), sorted_idx;
- cv::sortIdx(var_imp, sorted_idx, CV_SORT_EVERY_ROW +
- CV_SORT_DESCENDING);
- printf( "variable importance:\n" );
- int i, n = (int)var_imp.total();
- int type = var_imp.type();
- CV_Assert(type == CV_32F || type == CV_64F);
- for( i = 0; i < n; i++)
- {
- int k = sorted_idx.at<int>(i);
- printf( "%d\t%f\n", k, type == CV_32F ?
- var_imp.at<float>(k) :
- var_imp.at<double>(k));
- }
- }
- printf("\n");
- }
- int main()
- {
- const char* filename = "data.xml";
- int response_idx = 0;
- CvMLData data;
- data.read_csv( filename ); // read data
- data.set_response_idx( response_idx ); // set response index
- data.change_var_type( response_idx,
- CV_VAR_CATEGORICAL ); // set response type
- // split train and test data
- CvTrainTestSplit spl( 0.5f );
- data.set_train_test_split( &spl );
- data.set_miss_ch("?"); // set missing value
- CvRTrees rtrees;
- rtrees.train( &data, CvRTParams( 10, 2, 0, false,
- 16, 0, true, 0, 100, 0, CV_TERMCRIT_ITER ));
- print_result( rtrees.calc_error( &data, CV_TRAIN_ERROR),
- rtrees.calc_error( &data, CV_TEST_ERROR ),
- rtrees.get_var_importance() );
- return 0;
- }
References:
[1] OpenCV 2.3 Online Documentation: http://opencv.itseez.com/modules/ml/doc/random_trees.html
[2] Random Forests, Leo Breiman and Adele Cutler: http://www.stat.berkeley.edu/users/breiman/RandomForests/cc_home.htm
[3] T. Hastie, R. Tibshirani, J. H. Friedman. The Elements of Statistical Learning. ISBN-13 978-0387952840, 2003, Springer.
源码细节:
● 训练函数
const CvMat* _responses, const CvMat* _var_idx,
const CvMat* _sample_idx, const CvMat* _var_type,
const CvMat* _missing_mask, CvRTParams params )
Step1:清理现场,调用clear()函数,删除和释放所有决策树,清除训练数据等;
Step2:构造适用于单棵决策树训练的参数包CvDTreeParams,主要就是对CvRTParams中一些参数的拷贝;
Step3:构建训练数据CvDTreeTrainData,主要涉及CvDTreeTrainData::set_data()函数。CvDTreeTrainData包含CvDTreeParams格式的参数包、被所有树共享的训练数据(优化结构使最优分裂更迅速)以及response类型和类数目等常用数据,还包括最终构造出来的树节点缓存等。
Step4:检查CvRTParams::nactive_vars使其不大于最大启用变量数;若nactive_vars传参为0,则默认赋值为最大启用变量数的平方根;若小于0,则报错退出;
Step5:创建并初始化一个变量活跃Mask(1×变量总数),初始化过程设置前nactive_vars个变量mask为1(活跃),其余为0(非活跃);
Step6:调用CvRTrees::grow_forest()开始生成森林。
● 生成森林
Step1:如果需要以准确率为终止条件或者需要计算变量的重要值(is_oob_or_vimportance = true),则需要创建并初始化以下数据:
oob_sample_votes 用于分类问题,样本数量×类数量,存储每个样本的测试分类;
oob_responses 用于回归问题,2×样本数量,这是一个不直接使用的数据,旨在为以下两个数据开辟空间;
oob_predictions_sum 用于回归问题,1×样本数量,存储每个样本的预测值之和;
oob_num_of_predictions 用于回归问题,1×样本数量,存储每个样本被预测的次数;
oob_samples_perm_ptr 用于存储乱序样本,样本数量×类数量;
samples_ptr / missing_ptr / true_resp_ptr 从训练数据中拷贝的样本数组、缺失Mask和真实response数组;
maximal_response response的最大绝对值。
Step2:初始化以下数据:
trees CvForestTree格式的单棵树集合,共max_ntrees棵,max_ntrees由CvDTreeParams定义;
sample_idx_mask_for_tree 存储每个样本是否参与当前树的构建,1×样本数量;
sample_idx_for_tree 存储在构建当前树时参与的样本序号,1×样本数量;
Step3:随机生成参与当前树构建的样本集(sample_idx_for_tree定义),调用CvForestTree::train()函数生成当前树,加入树集合中。CvForestTree::train()先调用CvDTreeTrainData::subsample_data()函数整理样本集,再通过调用CvForestTree::try_split_node()完成树的生成,try_split_node是一个递归函数,在分割当前节点后,会调用分割左右节点的try_split_node函数,直到准确率达到标准或者节点样本数过少;
Step4:如果需要以准确率为终止条件或者需要计算变量的重要值(is_oob_or_vimportance = true),则:
使用未参与当前树构建的样本,测试当前树的预测准确率;
若需计算变量的重要值,对于每一种变量,对每一个非参与样本,替换其该位置的变量值为另一随机样本的该变量值,再进行预测,其正确率的统计值与上一步当前树的预测准确率的差,将会累计到该变量的重要值中;
Step5:重复Step3 – 4,直到终止条件;
Step6:若需计算变量的重要值,归一化变量重要性到[0, 1]。
●训练单棵树
Step1:调用CvDtree::calc_node_value()函数:对于分类问题,计算当前节点样本中最大样本数量的类别,最为该节点的类别,同时计算更新交叉验证错误率(命名带有cv_的数据);对于回归问题,也是类似的计算当前节点样本值的均值作为该节点的值,也计算更新交叉验证错误率;
Step2:作终止条件判断:样本数量是否过少;深度是否大于最大指定深度;对于分类问题,该节点是否只有一种类别;对于回归问题,交叉验证错误率是否已达到指定精度要求。若是,则停止分裂;
Step3:若可分裂,调用CvForestTree::find_best_split()函数寻找最优分裂,首先随机当前节点的活跃变量,再使用ForestTreeBestSplitFinder完成:ForestTreeBestSplitFinder对分类或回归问题、变量是否可数,分别处理。对于每个可用变量调用相应的find函数,获得针对某一变量的最佳分裂,再在这所有最佳分裂中依照quality值寻找最最优。find函数只关描述分类问题(回归其实差不多):
CvForestTree::find_split_ord_class():可数变量,在搜寻开始前,最主要的工作是建立一个按变量值升序的样本index序列,搜寻按照这个序列进行。最优分裂的依据是
![]()
也就是左右分裂所有类别中样本数量的平方 / 左右分裂的样本总数,再相加(= =还是公式看的懂些吧。。)
比如说,排序后的 A A B A B B C B C C 这样的序列,比较这样两种分裂方法:
A A B A B B | C B C C 和 A A B A B B C B | C C
第一种的quality是 (32 + 32 + 02) / 6 + (02 + 12 + 32) / 4 = 5.5
第二种的quality是 (32 + 42 + 12) / 8 + (02 + 02 + 22) / 2 = 5.25
第一种更优秀些。感性地看,第一种的左分裂只有AB,右分裂只有BC,那么可能再来一次分裂就能完全分辨;而第二种虽然右分裂只有C,但是左分裂一团糟,其实完全没做什么事情。
最优搜寻过程中会跳过一些相差很小的以及不活跃的变量值,主要是为了避免在连续变量取值段出现分裂,这在真实预测中会降低树的鲁棒性。
CvForestTree::find_split_cat_class():不可数变量,分裂quality的计算与可数情况相似,不同的是分类的标准,不再是阈值对数值的左右划分,而是对变量取值的子集划分,比如将a b c d e五种可取变量值分为{a} + {b, c, d, e}、{a, b} + {c, d, e}等多种形式比较quality。统计的是左右分裂每个类别取该分裂子集中的变量值的样本数量的平方 / 左右分裂的样本总数,再相加。同样,搜寻会跳过样本数量很少的以及不活跃的分类取值。
Step4:若不存在最优分裂或者无法分裂,则释放相关数据后返回;否则,处理代理分裂、分割左右分裂数据、调用左右后续分裂。
References:
[1] OpenCV 2.3 Online Documentation: http://opencv.itseez.com/modules/ml/doc/random_trees.html
[2] Random Forests, Leo Breiman and Adele Cutler: http://www.stat.berkeley.edu/users/breiman/RandomForests/cc_home.htm
[3] T. Hastie, R. Tibshirani, J. H. Friedman. The Elements of Statistical Learning . ISBN-13 978-0387952840, 2003, Springer.
Random Forests
Leo Breiman and Adele Cutler
Random Forests(tm) is a trademark of Leo Breiman and Adele Cutler and is licensed exclusively to Salford Systems for the commercial release of the software.
Our trademarks also include RF(tm), RandomForests(tm), RandomForest(tm) and Random Forest(tm).
Contents
Introduction
Overview
Features of random forests
Remarks
How Random Forests work
The oob error estimate
Variable importance
Gini importance
Interactions
Proximities
Scaling
Prototypes
Missing values for the training set
Missing values for the test set
Mislabeled cases
Outliers
Unsupervised learning
Balancing prediction error
Detecting novelties
A case study - microarray data
Classification mode
Variable importance
Using important variables
Variable interactions
Scaling the data
Prototypes
Outliers
A case study - dna data
Missing values in the training set
Missing values in the test set
Mislabeled cases
Case Studies for unsupervised learning
Clustering microarray data
Clustering dna data
Clustering glass data
Clustering spectral data
References
Introduction
This section gives a brief overview of random forests and some comments about the features of the method.
Overview
We assume that the user knows about the construction of single classification trees. Random Forests grows many classification trees. To classify a new object from an input vector, put the input vector down each of the trees in the forest. Each tree gives a classification, and we say the tree "votes" for that class. The forest chooses the classification having the most votes (over all the trees in the forest).
Each tree is grown as follows:
- If the number of cases in the training set is N, sample N cases at random - but with replacement, from the original data. This sample will be the training set for growing the tree.
- If there are M input variables, a number m<<M is specified such that at each node, m variables are selected at random out of the M and the best split on these m is used to split the node. The value of m is held constant during the forest growing.
- Each tree is grown to the largest extent possible. There is no pruning.
In the original paper on random forests, it was shown that the forest error rate depends on two things:
- The correlation between any two trees in the forest. Increasing the correlation increases the forest error rate.
- The strength of each individual tree in the forest. A tree with a low error rate is a strong classifier. Increasing the strength of the individual trees decreases the forest error rate.
Reducing m reduces both the correlation and the strength. Increasing it increases both. Somewhere in between is an "optimal" range of m - usually quite wide. Using the oob error rate (see below) a value of m in the range can quickly be found. This is the only adjustable parameter to which random forests is somewhat sensitive.
Features of Random Forests
- It is unexcelled in accuracy among current algorithms.
- It runs efficiently on large data bases.
- It can handle thousands of input variables without variable deletion.
- It gives estimates of what variables are important in the classification.
- It generates an internal unbiased estimate of the generalization error as the forest building progresses.
- It has an effective method for estimating missing data and maintains accuracy when a large proportion of the data are missing.
- It has methods for balancing error in class population unbalanced data sets.
- Generated forests can be saved for future use on other data.
- Prototypes are computed that give information about the relation between the variables and the classification.
- It computes proximities between pairs of cases that can be used in clustering, locating outliers, or (by scaling) give interesting views of the data.
- The capabilities of the above can be extended to unlabeled data, leading to unsupervised clustering, data views and outlier detection.
- It offers an experimental method for detecting variable interactions.
Remarks
Random forests does not overfit. You can run as many trees as you want. It is fast. Running on a data set with 50,000 cases and 100 variables, it produced 100 trees in 11 minutes on a 800Mhz machine. For large data sets the major memory requirement is the storage of the data itself, and three integer arrays with the same dimensions as the data. If proximities are calculated, storage requirements grow as the number of cases times the number of trees.
How random forests work
To understand and use the various options, further information about how they are computed is useful. Most of the options depend on two data objects generated by random forests.
When the training set for the current tree is drawn by sampling with replacement, about one-third of the cases are left out of the sample. This oob (out-of-bag) data is used to get a running unbiased estimate of the classification error as trees are added to the forest. It is also used to get estimates of variable importance.
After each tree is built, all of the data are run down the tree, and proximities are computed for each pair of cases. If two cases occupy the same terminal node, their proximity is increased by one. At the end of the run, the proximities are normalized by dividing by the number of trees. Proximities are used in replacing missing data, locating outliers, and producing illuminating low-dimensional views of the data.
The out-of-bag (oob) error estimate
In random forests, there is no need for cross-validation or a separate test set to get an unbiased estimate of the test set error. It is estimated internally, during the run, as follows:
Each tree is constructed using a different bootstrap sample from the original data. About one-third of the cases are left out of the bootstrap sample and not used in the construction of the kth tree.
Put each case left out in the construction of the kth tree down the kth tree to get a classification. In this way, a test set classification is obtained for each case in about one-third of the trees. At the end of the run, take j to be the class that got most of the votes every time case n was oob. The proportion of times that j is not equal to the true class of n averaged over all cases is the oob error estimate. This has proven to be unbiased in many tests.
Variable importance
In every tree grown in the forest, put down the oob cases and count the number of votes cast for the correct class. Now randomly permute the values of variable m in the oob cases and put these cases down the tree. Subtract the number of votes for the correct class in the variable-m-permuted oob data from the number of votes for the correct class in the untouched oob data. The average of this number over all trees in the forest is the raw importance score for variable m.
If the values of this score from tree to tree are independent, then the standard error can be computed by a standard computation. The correlations of these scores between trees have been computed for a number of data sets and proved to be quite low, therefore we compute standard errors in the classical way, divide the raw score by its standard error to get a z-score, ands assign a significance level to the z-score assuming normality.
If the number of variables is very large, forests can be run once with all the variables, then run again using only the most important variables from the first run.
For each case, consider all the trees for which it is oob. Subtract the percentage of votes for the correct class in the variable-m-permuted oob data from the percentage of votes for the correct class in the untouched oob data. This is the local importance score for variable m for this case, and is used in the graphics program RAFT.
Gini importance
Every time a split of a node is made on variable m the gini impurity criterion for the two descendent nodes is less than the parent node. Adding up the gini decreases for each individual variable over all trees in the forest gives a fast variable importance that is often very consistent with the permutation importance measure.
Interactions
The operating definition of interaction used is that variables m and k interact if a split on one variable, say m, in a tree makes a split on k either systematically less possible or more possible. The implementation used is based on the gini values g(m) for each tree in the forest. These are ranked for each tree and for each two variables, the absolute difference of their ranks are averaged over all trees.
This number is also computed under the hypothesis that the two variables are independent of each other and the latter subtracted from the former. A large positive number implies that a split on one variable inhibits a split on the other and conversely. This is an experimental procedure whose conclusions need to be regarded with caution. It has been tested on only a few data sets.
Proximities
These are one of the most useful tools in random forests. The proximities originally formed a NxN matrix. After a tree is grown, put all of the data, both training and oob, down the tree. If cases k and n are in the same terminal node increase their proximity by one. At the end, normalize the proximities by dividing by the number of trees.
Users noted that with large data sets, they could not fit an NxN matrix into fast memory. A modification reduced the required memory size to NxT where T is the number of trees in the forest. To speed up the computation-intensive scaling and iterative missing value replacement, the user is given the option of retaining only the nrnn largest proximities to each case.
When a test set is present, the proximities of each case in the test set with each case in the training set can also be computed. The amount of additional computing is moderate.
Scaling
The proximities between cases n and k form a matrix {prox(n,k)}. From their definition, it is easy to show that this matrix is symmetric, positive definite and bounded above by 1, with the diagonal elements equal to 1. It follows that the values 1-prox(n,k) are squared distances in a Euclidean space of dimension not greater than the number of cases. For more background on scaling see "Multidimensional Scaling" by T.F. Cox and M.A. Cox.
Let prox(-,k) be the average of prox(n,k) over the 1st coordinate, prox(n,-) be the average of prox(n,k) over the 2nd coordinate, and prox(-,-) the average over both coordinates. Then the matrix
- cv(n,k)=.5*(prox(n,k)-prox(n,-)-prox(-,k)+prox(-,-))
is the matrix of inner products of the distances and is also positive definite symmetric. Let the eigenvalues of cv be l(j) and the eigenvectors nj(n). Then the vectors
x(n) = (Öl(1) n1(n) , Öl(2) n2(n) , ...,)
have squared distances between them equal to 1-prox(n,k). The values of Öl(j) nj(n) are referred to as the jth scaling coordinate.
In metric scaling, the idea is to approximate the vectors x(n) by the first few scaling coordinates. This is done in random forests by extracting the largest few eigenvalues of the cv matrix, and their corresponding eigenvectors . The two dimensional plot of the ith scaling coordinate vs. the jth often gives useful information about the data. The most useful is usually the graph of the 2nd vs. the 1st.
Since the eigenfunctions are the top few of an NxN matrix, the computational burden may be time consuming. We advise taking nrnn considerably smaller than the sample size to make this computation faster.
There are more accurate ways of projecting distances down into low dimensions, for instance the Roweis and Saul algorithm. But the nice performance, so far, of metric scaling has kept us from implementing more accurate projection algorithms. Another consideration is speed. Metric scaling is the fastest current algorithm for projecting down.
Generally three or four scaling coordinates are sufficient to give good pictures of the data. Plotting the second scaling coordinate versus the first usually gives the most illuminating view.
Prototypes
Prototypes are a way of getting a picture of how the variables relate to the classification. For the jth class, we find the case that has the largest number of class j cases among its k nearest neighbors, determined using the proximities. Among these k cases we find the median, 25th percentile, and 75th percentile for each variable. The medians are the prototype for class j and the quartiles give an estimate of is stability. For the second prototype, we repeat the procedure but only consider cases that are not among the original k, and so on. When we ask for prototypes to be output to the screen or saved to a file, prototypes for continuous variables are standardized by subtractng the 5th percentile and dividing by the difference between the 95th and 5th percentiles. For categorical variables, the prototype is the most frequent value. When we ask for prototypes to be output to the screen or saved to a file, all frequencies are given for categorical variables.
Missing value replacement for the training set
Random forests has two ways of replacing missing values. The first way is fast. If the mth variable is not categorical, the method computes the median of all values of this variable in class j, then it uses this value to replace all missing values of the mth variable in class j. If the mth variable is categorical, the replacement is the most frequent non-missing value in class j. These replacement values are called fills.
The second way of replacing missing values is computationally more expensive but has given better performance than the first, even with large amounts of missing data. It replaces missing values only in the training set. It begins by doing a rough and inaccurate filling in of the missing values. Then it does a forest run and computes proximities.
If x(m,n) is a missing continuous value, estimate its fill as an average over the non-missing values of the mth variables weighted by the proximities between the nth case and the non-missing value case. If it is a missing categorical variable, replace it by the most frequent non-missing value where frequency is weighted by proximity.
Now iterate-construct a forest again using these newly filled in values, find new fills and iterate again. Our experience is that 4-6 iterations are enough.
Missing value replacement for the test set
When there is a test set, there are two different methods of replacement depending on whether labels exist for the test set.
If they do, then the fills derived from the training set are used as replacements. If labels no not exist, then each case in the test set is replicated nclass times (nclass= number of classes). The first replicate of a case is assumed to be class 1 and the class one fills used to replace missing values. The 2nd replicate is assumed class 2 and the class 2 fills used on it.
This augmented test set is run down the tree. In each set of replicates, the one receiving the most votes determines the class of the original case.
Mislabeled cases
The training sets are often formed by using human judgment to assign labels. In some areas this leads to a high frequency of mislabeling. Many of the mislabeled cases can be detected using the outlier measure. An example is given in the DNA case study.
Outliers
Outliers are generally defined as cases that are removed from the main body of the data. Translate this as: outliers are cases whose proximities to all other cases in the data are generally small. A useful revision is to define outliers relative to their class. Thus, an outlier in class j is a case whose proximities to all other class j cases are small.
Define the average proximity from case n in class j to the rest of the training data class j as:

The raw outlier measure for case n is defined as
![]()
This will be large if the average proximity is small. Within each class find the median of these raw measures, and their absolute deviation from the median. Subtract the median from each raw measure, and divide by the absolute deviation to arrive at the final outlier measure.
Unsupervised learning
In unsupervised learning the data consist of a set of x -vectors of the same dimension with no class labels or response variables. There is no figure of merit to optimize, leaving the field open to ambiguous conclusions. The usual goal is to cluster the data - to see if it falls into different piles, each of which can be assigned some meaning.
The approach in random forests is to consider the original data as class 1 and to create a synthetic second class of the same size that will be labeled as class 2. The synthetic second class is created by sampling at random from the univariate distributions of the original data. Here is how a single member of class two is created - the first coordinate is sampled from the N values {x(1,n)}. The second coordinate is sampled independently from the N values {x(2,n)}, and so forth.
Thus, class two has the distribution of independent random variables, each one having the same univariate distribution as the corresponding variable in the original data. Class 2 thus destroys the dependency structure in the original data. But now, there are two classes and this artificial two-class problem can be run through random forests. This allows all of the random forests options to be applied to the original unlabeled data set.
If the oob misclassification rate in the two-class problem is, say, 40% or more, it implies that the x -variables look too much like independent variables to random forests. The dependencies do not have a large role and not much discrimination is taking place. If the misclassification rate is lower, then the dependencies are playing an important role.
Formulating it as a two class problem has a number of payoffs. Missing values can be replaced effectively. Outliers can be found. Variable importance can be measured. Scaling can be performed (in this case, if the original data had labels, the unsupervised scaling often retains the structure of the original scaling). But the most important payoff is the possibility of clustering.
Balancing prediction error
In some data sets, the prediction error between classes is highly unbalanced. Some classes have a low prediction error, others a high. This occurs usually when one class is much larger than another. Then random forests, trying to minimize overall error rate, will keep the error rate low on the large class while letting the smaller classes have a larger error rate. For instance, in drug discovery, where a given molecule is classified as active or not, it is common to have the actives outnumbered by 10 to 1, up to 100 to 1. In these situations the error rate on the interesting class (actives) will be very high.
The user can detect the imbalance by outputs the error rates for the individual classes. To illustrate 20 dimensional synthetic data is used. Class 1 occurs in one spherical Gaussian, class 2 on another. A training set of 1000 class 1's and 50 class 2's is generated, together with a test set of 5000 class 1's and 250 class 2's.
The final output of a forest of 500 trees on this data is:
500 3.7 0.0 78.4
There is a low overall test set error (3.73%) but class 2 has over 3/4 of its cases misclassified.
The error can balancing can be done by setting different weights for the classes.
The higher the weight a class is given, the more its error rate is decreased. A guide as to what weights to give is to make them inversely proportional to the class populations. So set weights to 1 on class 1, and 20 on class 2, and run again. The output is:
500 12.1 12.7 0.0
The weight of 20 on class 2 is too high. Set it to 10 and try again, getting:
500 4.3 4.2 5.2
This is pretty close to balance. If exact balance is wanted, the weight on class 2 could be jiggled around a bit more.
Note that in getting this balance, the overall error rate went up. This is the usual result - to get better balance, the overall error rate will be increased.
Detecting novelties
The outlier measure for the test set can be used to find novel cases not fitting well into any previously established classes.
The satimage data is used to illustrate. There are 4435 training cases, 2000 test cases, 36 variables and 6 classes.
In the experiment five cases were selected at equal intervals in the test set. Each of these cases was made a "novelty" by replacing each variable in the case by the value of the same variable in a randomly selected training case. The run is done using noutlier =2, nprox =1. The output of the run is graphed below:

This shows that using an established training set, test sets can be run down and checked for novel cases, rather than running the training set repeatedly. The training set results can be stored so that test sets can be run through the forest without reconstructing it.
This method of checking for novelty is experimental. It may not distinguish novel cases on other data. For instance, it does not distinguish novel cases in the dna test data.
A case study-microarray data
To give an idea of the capabilities of random forests, we illustrate them on an early microarray lymphoma data set with 81 cases, 3 classes, and 4682 variables corresponding to gene expressions.
Classification mode
To do a straight classification run, use the settings:
parameter(
c DESCRIBE DATA
1 mdim=4682, nsample0=81, nclass=3, maxcat=1,
1 ntest=0, labelts=0, labeltr=1,
c
c SET RUN PARAMETERS
2 mtry0=150, ndsize=1, jbt=1000, look=100, lookcls=1,
2 jclasswt=0, mdim2nd=0, mselect=0, iseed=4351,
c
c SET IMPORTANCE OPTIONS
3 imp=0, interact=0, impn=0, impfast=0,
c
c SET PROXIMITY COMPUTATIONS
4 nprox=0, nrnn=5,
c
c SET OPTIONS BASED ON PROXIMITIES
5 noutlier=0, nscale=0, nprot=0,
c
c REPLACE MISSING VALUES
6 code=-999, missfill=0, mfixrep=0,
c
c GRAPHICS
7 iviz=1,
c
c SAVING A FOREST
8 isaverf=0, isavepar=0, isavefill=0, isaveprox=0,
c
c RUNNING A SAVED FOREST
9 irunrf=0, ireadpar=0, ireadfill=0, ireadprox=0)
Note: since the sample size is small, for reliability 1000 trees are grown using mtry0=150. The results are not sensitive to mtry0 over the range 50-200. Since look=100, the oob results are output every 100 trees in terms of percentage misclassified
100 2.47
200 2.47
300 2.47
400 2.47
500 1.23
600 1.23
700 1.23
800 1.23
900 1.23
1000 1.23
(note: an error rate of 1.23% implies 1 of the 81 cases was misclassified,)
Variable importance
The variable importances are critical. The run computing importances is done by switching imp =0 to imp =1 in the above parameter list. The output has four columns:
gene number the raw importance score the z-score obtained by dividing the raw score by its standard error the significance level.
The highest 25 gene importances are listed sorted by their z-scores. To get the output on a disk file, put impout =1, and give a name to the corresponding output file. If impout is put equal to 2 the results are written to screen and you will see a display similar to that immediately below:
gene raw z-score significance number score 667 1.414 1.069 0.143 689 1.259 0.961 0.168 666 1.112 0.903 0.183 668 1.031 0.849 0.198 682 0.820 0.803 0.211 878 0.649 0.736 0.231 1080 0.514 0.729 0.233 1104 0.514 0.718 0.237 879 0.591 0.713 0.238 895 0.519 0.685 0.247 3621 0.552 0.684 0.247 3529 0.650 0.683 0.247 3404 0.453 0.661 0.254 623 0.286 0.655 0.256 3617 0.498 0.654 0.257 650 0.505 0.650 0.258 645 0.380 0.644 0.260 3616 0.497 0.636 0.262 938 0.421 0.635 0.263 915 0.426 0.631 0.264 669 0.484 0.626 0.266 663 0.550 0.625 0.266 723 0.334 0.610 0.271 685 0.405 0.605 0.272 3631 0.402 0.603 0.273
Using important variables
Another useful option is to do an automatic rerun using only those variables that were most important in the original run. Say we want to use only the 15 most important variables found in the first run in the second run. Then in the options change mdim2nd=0 to mdim2nd=15 , keep imp=1 and compile. Directing output to screen, you will see the same output as above for the first run plus the following output for the second run. Then the importances are output for the 15 variables used in the 2nd run.
gene raw z-score significance
number score
3621 6.235 2.753 0.003
1104 6.059 2.709 0.003
3529 5.671 2.568 0.005
666 7.837 2.389 0.008
3631 4.657 2.363 0.009
667 7.005 2.275 0.011
668 6.828 2.255 0.012
689 6.637 2.182 0.015
878 4.733 2.169 0.015
682 4.305 1.817 0.035
644 2.710 1.563 0.059
879 1.750 1.283 0.100
686 1.937 1.261 0.104
1080 0.927 0.906 0.183
623 0.564 0.847 0.199
Variable interactions
Another option is looking at interactions between variables. If variable m1 is correlated with variable m2 then a split on m1 will decrease the probability of a nearby split on m2 . The distance between splits on any two variables is compared with their theoretical difference if the variables were independent. The latter is subtracted from the former-a large resulting value is an indication of a repulsive interaction. To get this output, change interact =0 to interact=1 leaving imp =1 and mdim2nd =10.
The output consists of a code list: telling us the numbers of the genes corresponding to id. 1-10. The interactions are rounded to the closest integer and given in the matrix following two column list that tells which gene number is number 1 in the table, etc.
1 2 3 4 5 6 7 8 9 10
1 0 13 2 4 8 -7 3 -1 -7 -2
2 13 0 11 14 11 6 3 -1 6 1
3 2 11 0 6 7 -4 3 1 1 -2
4 4 14 6 0 11 -2 1 -2 2 -4
5 8 11 7 11 0 -1 3 1 -8 1
6 -7 6 -4 -2 -1 0 7 6 -6 -1
7 3 3 3 1 3 7 0 24 -1 -1
8 -1 -1 1 -2 1 6 24 0 -2 -3
9 -7 6 1 2 -8 -6 -1 -2 0 -5
10 -2 1 -2 -4 1 -1 -1 -3 -5 0
There are large interactions between gene 2 and genes 1,3,4,5 and between 7 and 8.
Scaling the data
The wish of every data analyst is to get an idea of what the data looks like. There is an excellent way to do this in random forests.
Using metric scaling the proximities can be projected down onto a low dimensional Euclidian space using "canonical coordinates". D canonical coordinates will project onto a D-dimensional space. To get 3 canonical coordinates, the options are as follows:
parameter(
c DESCRIBE DATA
1 mdim=4682, nsample0=81, nclass=3, maxcat=1,
1 ntest=0, labelts=0, labeltr=1,
c
c SET RUN PARAMETERS
2 mtry0=150, ndsize=1, jbt=1000, look=100, lookcls=1,
2 jclasswt=0, mdim2nd=0, mselect=0, iseed=4351,
c
c SET IMPORTANCE OPTIONS
3 imp=0, interact=0, impn=0, impfast=0,
c
c SET PROXIMITY COMPUTATIONS
4 nprox=1, nrnn=50,
c
c SET OPTIONS BASED ON PROXIMITIES
5 noutlier=0, nscale=3, nprot=0,
c
c REPLACE MISSING VALUES
6 code=-999, missfill=0, mfixrep=0,
c
c GRAPHICS
7 iviz=1,
c
c SAVING A FOREST
8 isaverf=0, isavepar=0, isavefill=0, isaveprox=0,
c
c RUNNING A SAVED FOREST
9 irunrf=0, ireadpar=0, ireadfill=0, ireadprox=0)
Note that imp and mdim2nd have been set back to zero and nscale set equal to 3. nrnn is set to 50 which instructs the program to compute the 50 largest proximities for each case. Set iscaleout=1. Compiling gives an output with nsample rows and these columns giving case id, true class, predicted class and 3 columns giving the values of the three scaling coordinates. Plotting the 2nd canonical coordinate vs. the first gives:

The three classes are very distinguishable. Note: if one tries to get this result by any of the present clustering algorithms, one is faced with the job of constructing a distance measure between pairs of points in 4682-dimensional space - a low payoff venture. The plot above, based on proximities, illustrates their intrinsic connection to the data.
Prototypes
Two prototypes are computed for each class in the microarray data
The settings are mdim2nd=15, nprot=2, imp=1, nprox=1, nrnn=20. The values of the variables are normalized to be between 0 and 1. Here is the graph

Outliers
An outlier is a case whose proximities to all other cases are small. Using this idea, a measure of outlyingness is computed for each case in the training sample. This measure is different for the different classes. Generally, if the measure is greater than 10, the case should be carefully inspected. Other users have found a lower threshold more useful. To compute the measure, set nout =1, and all other options to zero. Here is a plot of the measure:

There are two possible outliers-one is the first case in class 1, the second is the first case in class 2.
A case study-dna data
There are other options in random forests that we illustrate using the dna data set. There are 60 variables, all four-valued categorical, three classes, 2000 cases in the training set and 1186 in the test set. This is a classic machine learning data set and is described more fully in the 1994 book "Machine learning, Neural and Statistical Classification" editors Michie, D., Spiegelhalter, D.J. and Taylor, C.C.
This data set is interesting as a case study because the categorical nature of the prediction variables makes many other methods, such as nearest neighbors, difficult to apply.
Missing values in the training set
To illustrate the options for missing value fill-in, runs were done on the dna data after deleting 10%, 20%, 30%, 40%, and 50% of the set data at random. Both methods missfill=1 andmfixrep=5 were used. The results are given in the graph below.

It is remarkable how effective the mfixrep process is. Similarly effective results have been obtained on other data sets. Here nrnn=5 is used. Larger values of nrnn do not give such good results.
At the end of the replacement process, it is advisable that the completed training set be downloaded by setting idataout =1.
Missing values in the test set
In v5, the only way to replace missing values in the test set is to set missfill =2 with nothing else on. Depending on whether the test set has labels or not, missfill uses different strategies. In both cases it uses the fill values obtained by the run on the training set.
We measure how good the fill of the test set is by seeing what error rate it assigns to the training set (which has no missing). If the test set is drawn from the same distribution as the training set, it gives an error rate of 3.7%. As the proportion of missing increases, using a fill drifts the distribution of the test set away from the training set and the test set error rate will increase.
We can check the accuracy of the fill for no labels by using the dna data, setting labelts=0, but then checking the error rate between the classes filled in and the true labels.
missing% labelts=1 labelts=0 10 4.9 5.0 20 8.1 8.4 30 13.4 13.8 40 21.4 22.4 50 30.4 31.4
There is only a small loss in not having the labels to assist the fill.
Mislabeled Cases
The DNA data base has 2000 cases in the training set, 1186 in the test set, and 60 variables, all of which are four-valued categorical variables. In the training set, one hundred cases are chosen at random and their class labels randomly switched. The outlier measure is computed and is graphed below with the black squares representing the class-switched cases
Select the threshold as 2.73. Then 90 of the 100 cases with altered classes have outlier measure exceeding this threshold. Of the 1900 unaltered cases, 62 exceed threshold.

Case studies for unsupervised learning
Clustering microarray data
We give some examples of the effectiveness of unsupervised clustering in retaining the structure of the unlabeled data. The scaling for the microarray data has this picture:

Suppose that in the 81 cases the class labels are erased. But it we want to cluster the data to see if there was any natural conglomeration. Again, with a standard approach the problem is trying to get a distance measure between 4681 variables. Random forests uses as different tack.
Set labeltr =0 . A synthetic data set is constructed that also has 81 cases and 4681 variables but has no dependence between variables. The original data set is labeled class 1, the synthetic class 2.
If there is good separation between the two classes, i.e. if the error rate is low, then we can get some information about the original data. Set nprox=1, and iscale =D-1. Then the proximities in the original data set are computed and projected down via scaling coordinates onto low dimensional space. Here is the plot of the 2nd versus the first.

The three clusters gotten using class labels are still recognizable in the unsupervised mode. The oob error between the two classes is 16.0%. If a two stage is done with mdim2nd=15, the error rate drops to 2.5% and the unsupervised clusters are tighter.
Clustering dna data
The scaling pictures of the dna data is, both supervised and unsupervised, are interesting and appear below:


The structure of the supervised scaling is retained, although with a different rotation and axis scaling. The error between the two classes is 33%, indication lack of strong dependency.
Clustering glass data
A more dramatic example of structure retention is given by using the glass data set-another classic machine learning test bed. There are 214 cases, 9 variables and 6 classes. The labeled scaling gives this picture:

Erasing the labels results in this projection:

Clustering spectral data
Another example uses data graciously supplied by Merck that consists of the first 468 spectral intensities in the spectrums of 764 compounds. The challenge presented by Merck was to find small cohesive groups of outlying cases in this data. Using forests with labeltr=0, there was excellent separation between the two classes, with an error rate of 0.5%, indicating strong dependencies in the original data.
We looked at outliers and generated this plot.

This plot gives no indication of outliers. But outliers must be fairly isolated to show up in the outlier display. To search for outlying groups scaling coordinates were computed. The plot of the 2nd vs. the 1st is below:

This shows, first, that the spectra fall into two main clusters. There is a possibility of a small outlying group in the upper left hand corner. To get another picture, the 3rd scaling coordinate is plotted vs. the 1st.

The group in question is now in the lower left hand corner and its separation from the main body of the spectra has become more apparent.
References
The theoretical underpinnings of this program are laid out in the paper "Random Forests". It's available on the same web page as this manual. It was recently published in the Machine Learning Journal.

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








