从傅里叶级数到傅里叶变换

---

傅里叶级数

为什么要有傅里叶级数

傅里叶级数（Fourier Series）是用一系列正弦波（Sinusoid）来描述任何周期函数的一种方法。图1中的三条曲线分别是周期为1秒的方波，正弦波和三角波。由于正弦和余弦只有相位差，故统称正弦波。 

 
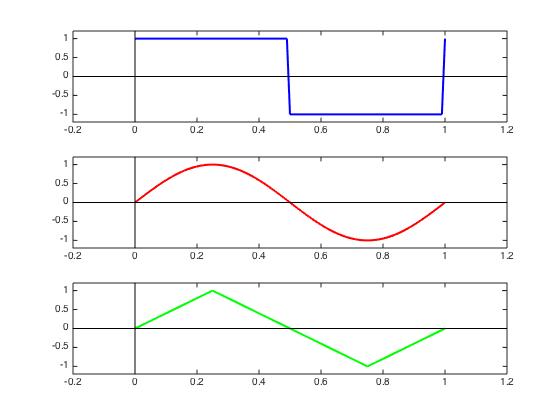
图1. 周期为1秒的方波，正弦波，三角波

在介绍傅里叶级数之前，让我们先来回顾一下级数的概念。级数是用一个无穷数列的加和来逼急一个数。函数项级数则是用一个函数列的加和来逼近一个函数。设 u1(x),u2(x),u3(x),⋯,un(x),⋯ 为定义在 (a,b) 内的函数序列。则 

∑n=1∞u(x)=u1(x)+u2(x)+u3(x)+⋯+un(x)+⋯

称为定义在 (a,b) 内的函数项级数。为什么要把一个看似简单的函数分解成一大堆函数的和呢？因为有些函数直接研究起来比较困难，以某种形式的级数进行展开，对里面的每一项单独研究，会变得更简单，也使得计算更加容易。级数有千千万万种，如泰勒级数，等比级数，调和级数等等。但是有一种由正弦函数组合而成的级数，显得尤为重要。这就是傅里叶级数。为什么傅里叶技术格外重要呢？这要归功于正弦函数优秀的性质。我们将函数展开成级数是为了获得更加简便和易于计算的形式。而当正弦波输入一个系统时，输出仍然是一个正弦波，只有振幅、相位和频率会发生变化，而不像其他的级数会使函数形式本身发生改变。这使得傅里叶级数在分析函数时具有了巨大的优势。此外，由于通信系统中电磁场与电磁波，以及诸多物理原理都与正弦信号有关，所以造就了傅里叶级数如此重要的地位。

傅里叶级数是怎么来的

傅里叶级数的得出

假如有两个周期函数（Periodic Function），它们的频率分别为 f1 和 f2 ，那么他们的叠加还是一个周期函数吗？频率又是多少呢？显然，两个不同频率的周期函数叠加仍然是一个周期函数，叠加后函数的周期是两个原函数周期的最小公倍数。因此，当一组频率为 1Hz,2Hz,3Hz,⋯,nHz,⋯ 的周期函数叠加时，叠加后的函数频率必然为 1Hz 。然而，如果采用了诸如 1.1Hz,2.5Hz,3,12435Hz 之类频率的级数项，则输出频率将陷入混乱，所以这里只选取如 1Hz,2Hz,3Hz,⋯,nHz,⋯ 的频率作为级数项。 1Hz 可以作为基本频率，改写作 fHz ， 则级数项将变为 fHz,2fHz,3fHz,⋯,nfHz,⋯ 。回想图1中周期为1秒的方波函数，我们可以将它表示成 

f(t)=∑n=0∞bn⋅sin(2π⋅n⋅t)n∈N

然而，上面我们所表示的函数恰好是一个周期为1秒的奇函数。如果用上面的公式来逼近一个偶函数则无法实现。所以，若 f(t) 是一个周期为1秒的偶函数，则 

f(t)=∑n=0∞an⋅cos(2π⋅n⋅t)n∈N

因此，当 f(t) 是一个周期为 T ，频率为 f 的一般函数，既有奇函数成分也有偶函数成分，此外，作为奇函数或偶函数对称点可能相对原点产生位移，易知这个位移不会影响函数的形状，可以用一个常数来表示，为了后续计算方便，这个位移记作 a02 ，则有 

f(t)=a02+∑n=0∞[ancos(2πfnt)＋bnsin(2πfnt)]n∈N

至此，我们已经得到了傅里叶级数的完整表达形式。

傅里叶级数中参数的确定与函数的正交性

那么如何确定上面公式中的 bn 呢？在这之前，然我们来谈谈什么是函数的正交性。学过线性代数的同学都知道，两个向量的正交是通过内积为零来定义的。而内积则是将向量的对应项相乘再求和来得到的。假设我们有一个任意长度的向量，每两个元素之间的距离无限小，那么我们就可以把这样两个向量看作两个连续的函数。类比内积的概念，两个函数正交也就是将两个函数赋予相同的自变量，再相乘，再做积分，如果积分等于零，则说明这两个函数在积分域上是正交的。

我们高兴的发现，不同频率的三角函数具有如下的正交性。其中 n,m∈N

∫T2−T2sin(2πfnt)sin(2πfmt)dt=⎧⎩⎨mcos(πTfm)sin(πTfn)−ncos(πTfn)sin(πTfm)πf(m2−n2)=0T2−sin(2πTfn)4πfn=T2n≠mn=m∫T2−T2cos(2πfnt)cos(2πfmt)dt=⎧⎩⎨mcos(πTfn)sin(πTfm)−ncos(πTfm)sin(πTfn)πf(m2−n2)=0T2+sin(2πTfm)4πfm=T2n≠mn=m∫T2−T2sin(2πfnt)cos(2πfmt)dt=0

因此，根据上述三角函数间的正交性，我们可以得出

∫T2−T2f(t)dt=a0T2∫T2−T2f(t)cos(2πfnt)dt=anT2∫T2−T2f(t)sin(2πfnt)dt=bnT2

至此，我们已经求得了所有傅里叶级数的参数。如下：

a0=2T∫T2−T2f(t)dtan=2T∫T2−T2f(t)cos(2πfnt)dtbn=2T∫T2−T2f(t)sin(2πfnt)dt

---

傅里叶变换

为什么要有傅里叶变换

在上一章，我们已经清楚的知道如何使用傅立叶级数去描述任何一个周期函数，其中傅里叶级数将一个周期函数描述成离散频率正弦函数的组合，即在频域上离散。然而，我们要分析的函数中常常会有非周期函数，这就需要傅里叶变换而不是傅里叶级数来描述这类函数。频域不同于时域，是从另一个角度观察客观世界的一种方式。其将无限动态的世界看成是注定的和静止的。从频域理解世界，更像是上帝看世界的方式。

对于任何一个非周期函数，我们都可以认为其可以通过一个周期函数的周期趋于无穷转化而来。周期趋于无穷也就意味着频率趋于零，以及角速度 ω 趋于零。也就是说，一个非周期函数会通过傅里叶变换被描述成连续的正弦函数的组合，即在频域上连续。基于这个思想，傅里叶级数即将演化成傅里叶变换。

从傅里叶级数到傅里叶变换

傅里叶级数的指数形式

让我们从傅里叶级数开始：

设在以 T 为周期的函数 fT(x) 的连续点处，级数的三角形式为 

fT(x)=a02+∑n=0∞[ancos(nωt)＋bnsin(nωt)]n∈N

式中，

ω=2πT=2πfa0=2T∫T2−T2f(t)dxan=2T∫T2−T2f(t)cos(2πfnt)dxbn=2T∫T2−T2f(t)sin(2πfnt)dx

为了以后计算的方便，这里使用欧拉公式将傅里叶级数中的正弦项和余弦项整合。

eiθ=cos(θ)+isin(θ)cos(θ)=eiθ+e−iθ2sin(θ)=eiθ−e−iθ2i=−i⋅eiθ−e−iθ2

将 sin(θ) 和 cos(θ) 代入傅里叶级数的表达式中，则

fT(x)=a02+∑n=0∞[aneinωt+e−inωt2−ibneinωt−e−inωt2]=a02+∑n=0∞[an−ibn2einωt+an+ibn2e−inωt]

令

c0cnc−nwn=a02=1T∫T2−T2fT(x)dx=an−ibn2=1T⎡⎣∫T2−T2fT(x)cos(nωx)dx−i∫T2−T2fT(x)sin(nωx)dx⎤⎦=1T∫T2−T2fT(x)[cos(nωx)−isin(nωx)]=1T∫T2−T2fT(x)[einωx+e−inωx2−i⋅(−i)⋅einωx−e−inωx2]=1T∫T2−T2fT(x)e−inωxdx=an+ibn2=1T∫T2−T2fT(x)einωxdx=nωn∈Z

代入 fT(x) 有 

fT(x)=c0+∑n=0∞(cneiwnx+c−ne−iwnx)=∑−∞+∞cneiwnx

至此，我们得到了傅里叶级数的指数形式

fT(x)=1T∑−∞+∞⎡⎣∫T2−T2fT(τ)e−iwnτdτ⎤⎦eiwnx

极限求得傅里叶变换

在为什么要有傅里叶级数一节中，我们已经说过傅里叶变换其实就是傅里叶级数的周期趋近于无穷。因此，假设我们的目标非周期函数为 f(x) ，由傅里叶级数逼近的周期函数为 fT(x) ，则

limT→+∞fT(x)=f(x)=limT→+∞1T∑−∞+∞⎡⎣∫T2−T2fT(τ)e−iwnτdτ⎤⎦eiwnx

当 n∈Z ，

Δw=wn−wn−1=2πTT=2πΔw

因此，当 T→+∞ 时，有 Δw→0 ，则

limT→+∞fT(x)=limΔw→012π∑−∞+∞⎡⎣∫T2−T2fT(τ)e−iwnτdτ⎤⎦eiwnxΔw

当 x 固定时， 12π[∫T2−T2fT(τ)e−iwnτdτ]eiwnx 是参数 w 的函数，记作 ΦT(w) ，即

ΦT(w)=12π⎡⎣∫T2−T2fT(τ)e−iwτdτ⎤⎦eiwx

因此，

f(x)=limΔw→0∑−∞+∞ΦT(w)Δw

当 T→+∞ ，即 ω→0 ， Δw→0 ， ΦT(w)→Φ(w) 。 
其中，

Φ(w)=12π[∫+∞−∞f(τ)e−iwτdτ]eiwx

此时 f(x) 可以看作 Φ(w) 在 (−∞,+∞) 上的积分， f(x)=∫+∞−∞Φ(w)dw ，即

f(x)=12π∫+∞−∞[∫+∞−∞f(τ)e−iwτdτ]eiwxdw

因此，将 x 替换成 t ，则 

F(ω)=∫+∞−∞f(τ)e−iwτdτ=F[f(τ)]f(t)=12π∫+∞−∞F(ω)eiωtdω=F−1[F(ω)]

从上面两个式子我们可以看出，第一个式子相当于将一个时域函数 f(τ) 变换成了频域函数 F(ω) ，而第二个式子相当于将频域函数 F(ω) 变换为时域函数 f(t) 。那么一个时域函数变换到频域后，再变换回时域，还是不是它自身呢？这个问题就相当于 f(τ)=f(t) 是否成立，也可以说成傅里叶变换是不是一一对应的。下面我们用反证法来探究这个问题。

假设傅里叶变换不是一一对应的。那么应该有

f(τ)≠f(t)

由于 f(τ) 进行傅里叶变换，为 F(ω) 。若假设成立， f(t) 的傅里叶变换应不一定为 F(ω) 。下面我们来计算 f(t) 的傅里叶变换。

F[f(t)]=F{12π∫+∞−∞[∫+∞−∞f(τ)e−iωτdτ]eiωtdω}=∫+∞−∞{12π∫+∞−∞[∫+∞−∞f(τ)e−iωτdτ]eiωtdω}e−iwtdt=F[f(τ)]

因此，假设不成立。傅里叶变换具有一一对应性。至此，我们已经完整的得到了傅立叶变换。

总结：傅里叶级数是傅里叶变换的逆函数

傅里叶级数在频域是相当于对应的余弦和正弦的系数，在时域就是三角函数求和值的连续显示，傅里叶变换正好相反