我们引入了一个新的深度神经网络模型家族。我们不指定隐藏层的离散序列，而是使用神经网络参数化隐藏状态的导数。利用黑盒微分方程解算器计算网络的输出。这些连续深度模型具有恒定的存储成本，根据每个输入调整其评估策略，并且可以明确地用数值精度换取速度。我们在连续深度残差网络和连续时间潜变量模型中证明了这些性质。我们还构建了连续规范化流程，这是一个可以通过最大似然进行训练的生成模型，无需对数据维度进行划分或排序。为了进行培训，我们展示了如何通过任何ODE求解器进行可伸缩的反向传播，而不需要访问其内部操作。这允许在较大的模型中进行端到端ode训练。
从序列变换到神经微分方程
多神经网络体系结构（如 RNN 或残差网络）包含重复的层块，这些层块能够有序保留信息，并通过学习函数在每一步中对其进行更改。一般来说，这种网络可以用下面的方程来描述：
因此，ht 是时间步长 t 的hidden信息，f（ht，θt）是当前隐藏信息和参数θ的学习函数
当我们添加更多的层、每一步更小的时候会发生什么？在极限的情况下，我们参数化隐藏神经元的连续动态（continuous dynamics），并使用一个神经网络指定的 ordinary differential equation (ODE)：
这个值可以由一个黑箱微分方程求解器计算，它评估隐藏神经元动力学f ff在任何需要的地方求解符合精度要求的解.
我们将ODE求解器视为一个黑盒，并使用伴随法计算梯度。这种方法通过在时间上反向求解第二个增强的ODE来计算梯度，并且适用于所有的ODE求解器。这种方法随问题的大小线性扩展，具有较低的内存成本，并显式地控制数值误差。
这个数量伴随着 ODE 的增加。
所有这三个积分都可以在一个ODE解算器的调用中计算出来，它将原始状态、伴随和其他偏导数连接到一个单独的向量。
连续归一化流
它们可以通过一系列非线性变换将简单的概率密度转换为复杂的概率密度，正如在神经网络中一样。因此，它们利用分布中的变量转换公式（类似于变分）
归一化流的一个常见应用是变分自动编码器（VAE），它通常假定潜在变量是高斯分布的。这一假设使得 VAE 的输出结果变差，因为它不允许网络学习所需的分布。对于归一化流，高斯参数可以在「解码」之前转换成各种各样的分布，从而提高 VAE 的生成能力
通过 ODE 生成时间序列模型
本文提到的第三个应用（可能是最重要的应用），是通过 ODE 进行时间序列建模。作者开始这项工作的动机之一是他们对不规则采样数据的兴趣，如医疗记录数据或网络流量数据。这种数据的离散化常常定义不明确，导致某些时间间隔内数据丢失或潜在变量不准确。有一些方法将时间信息连接到 RNN 的输入上，但这些方法并不能从根本上解决问题。
我们提出了一个连续时间，生成的方法建模时间序列。我们的模型用一个潜在的轨迹来表示每个时间序列
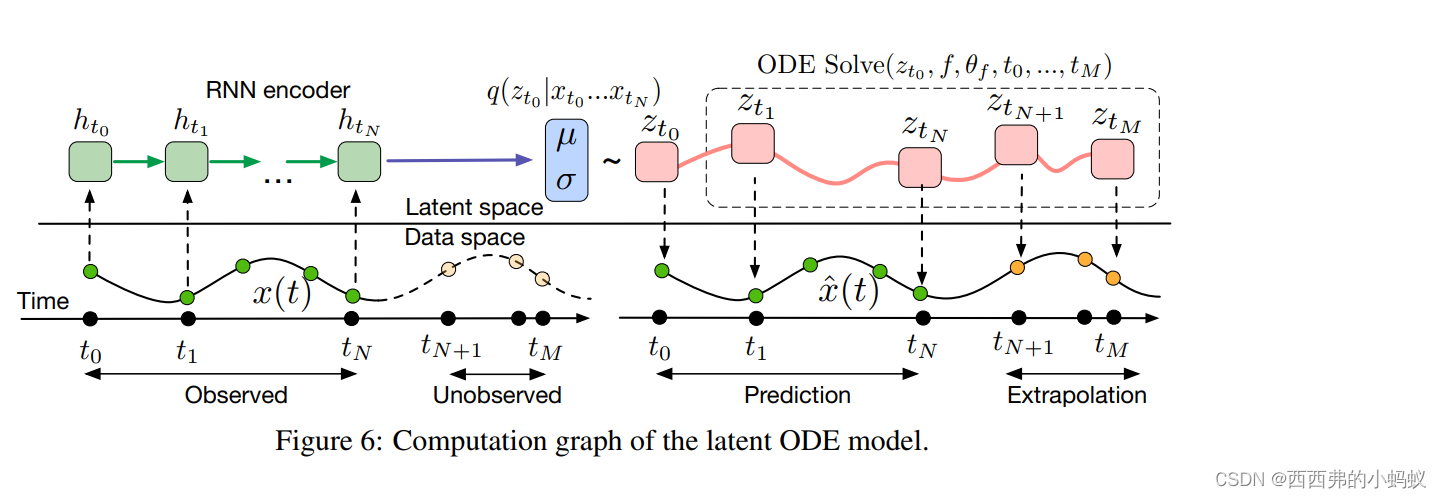
神经网络函数 f 负责计算从当前时间步长开始的任何时间 t 处的潜伏状态 z。该模型是一个变分自动编码器，它使用 RNN 在初始潜伏状态 z0 下编码过去的轨迹（在下图中为绿色）。与所有变分自动编码器一样，它通过分布的参数（在本例中，满足均值为μ、标准差为σ的高斯分布）来捕获潜在状态分布。从这个分布中，抽取一个样本并由 ODESolve 进行处理。
使用ode作为生成模型允许我们在连续的时间线上对任意时间点t1…tM做预测
结论
本文提出了一种非常有趣和新颖的神经网络思维方法。这可能是一篇开启深度学习新进化的里程碑式论文。我希望随着时间的推移，越来越多的研究人员开始从不同的角度来思考神经网络，正如本文所做的那样。
文中的方法是否确实适用于现有的各种模型、是否会被时间证明是有效的，仍有待观察。作者也提到了他们方法的一些局限性：
-
小批量可能是这种方法的一个问题，然而作者提到，即使在整个实验过程中使用小批量，评估的数量仍然是可以管理的。
-
只有当网络具有有限的权值并使用 Lipschitz 非线性函数（如 tanh 或 relu，而不是阶跃函数）时，才能保证 ODE 解的唯一性。
-
前向轨迹的可逆性可能会受到前向模式求解器中的数值误差、反向模式求解器中的数值误差以及由于多个初始值映射到同一结束状态而丢失的信息的综合影响。
作者还提到，他们的方法是不唯一的，残差网络作为近似的 ODE 求解器的想法已经过时了。此外，还有一些论文试图通过神经网络和高斯过程来学习不同的方程。
本文提出的方法的一个重要优点是，在评估或训练过程中，通过改变数值积分的精度，可以自由地调节速度和精确度之间的平衡。此外，该方法也非常适用（只要求神经网络的非线性是 Lipschitz 连续的），并且可以应用于时间序列建模、监督学习、密度估计或其他顺序过程。
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
