1.2.2 Logistic回归和梯度下降计算的数学流程

最新推荐文章于 2024-05-28 18:02:08 发布
最新推荐文章于 2024-05-28 18:02:08 发布
阅读量1.5k 收藏 2
点赞数 2
CC 4.0 BY-SA版权
分类专栏： 深度学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Einstellung/article/details/79506839
本文深入探讨Logistic回归的梯度下降法，通过计算图阐述前向和反向传播过程，利用链式法则求导，并详细解释如何应用于m个样本的梯度下降，最终展示算法的编程实现流程。

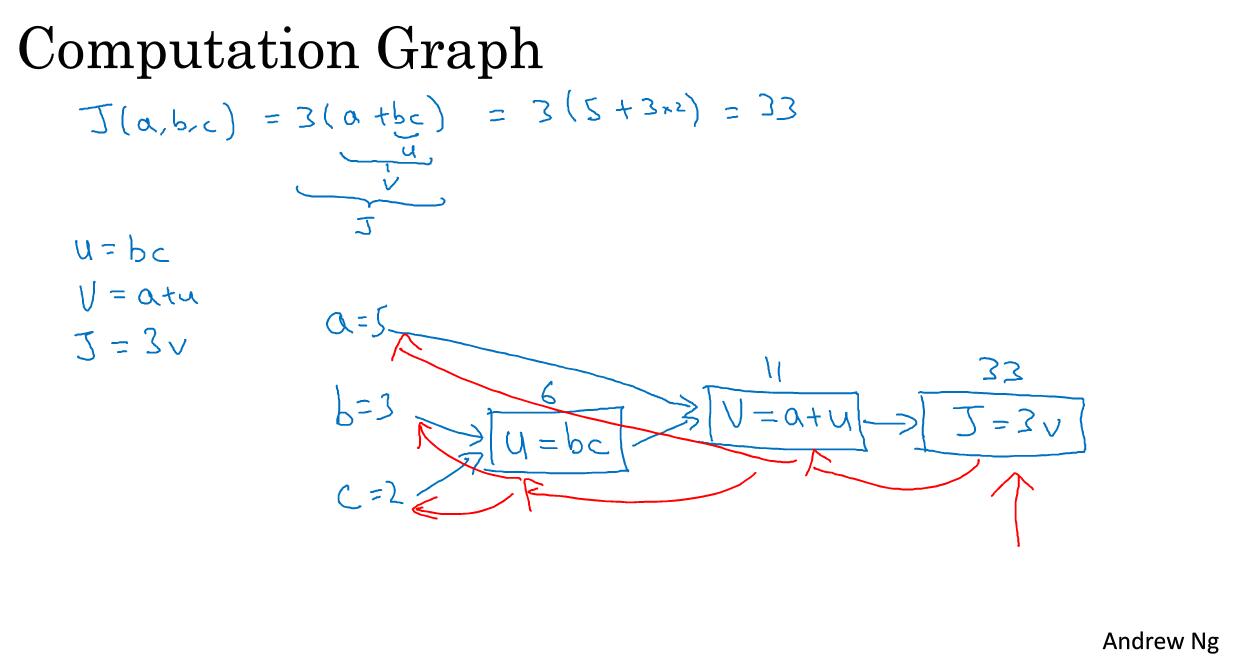
计算图

可以说，一个神经网络的计算都是按照前向或者反向传播过程来实现的，首先计算出神经网络的输出，紧接着一个反向传播的操作。后者，我们用来计算出对应的梯度或者导数。这个流程图解释了为什么用这样的方式来实现。

我们举一个更为简单的函数为例，如何计算该函数。具体流程如下：

这里写图片描述

流程图是用蓝色箭头画出来的，从左到右的计算过程。那么红色箭头是从右到左的导数计算过程。

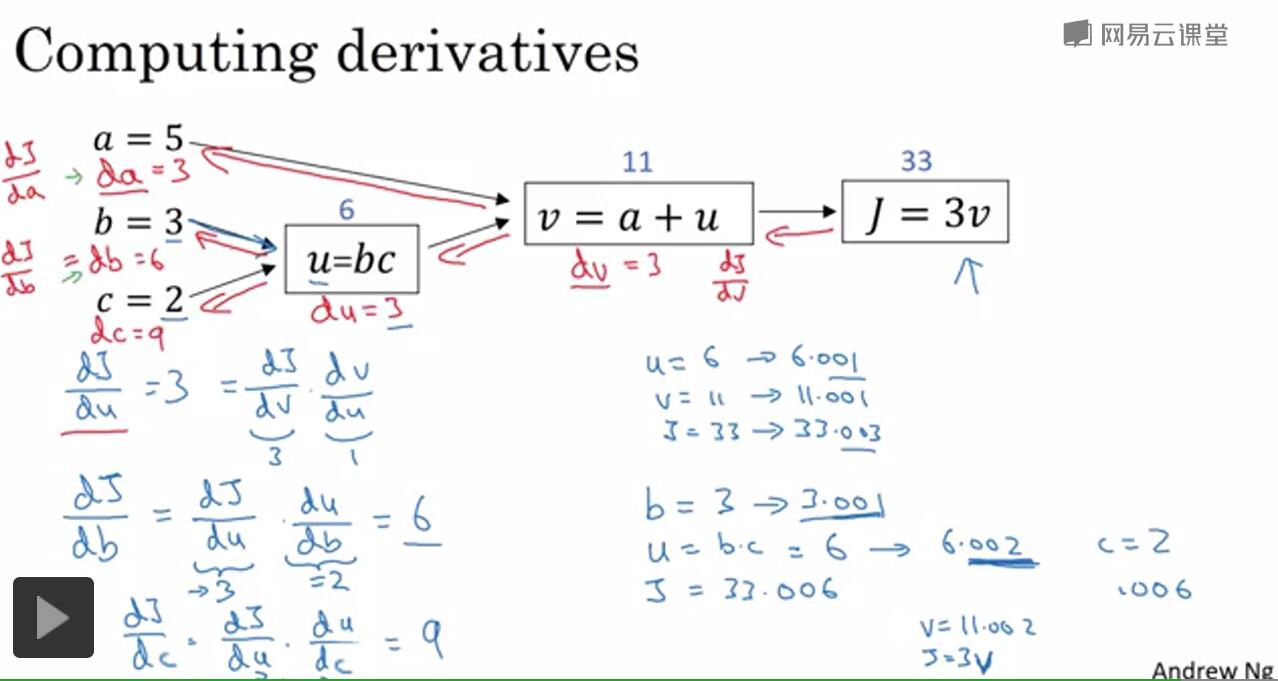
计算图的导数计算

反向传播算法的实质实际上就是用微积分的链式法则求导的过程。

这里写图片描述

比如说我们算dJ/da的大小，就用链式法则反过来算一下。

logistic回归的梯度下降法

这一部分将介绍如何用导数流程图来计算梯度。

我们回忆一下逻辑回归公式，注意这里的a是预测值的意思等于y

最低0.47元/天 解锁文章

200万优质内容无限畅学
梯度下降(Gradient Descent) 原理与代码实例讲解
AI大模型应用之禅
05-29 593
梯度下降(Gradient Descent) - 原理与代码实例讲解 作者：禅与计算机程序设计艺术 1. 背景介绍 1.1 机器学习中的优化问题 1.1
logistic回归的梯度计算
cs_wyong的博客
01-22 1460
在logistic回归中，假设我们的训练集由m个已标记样本组成：\[\{ ({x^{(1)}},{y^{(1)}}),...,({x^{(m)}},{y^{(m)}})\} \]且激活函数为sigmoid函数：\[{h_\theta }(x) = \frac{1}{{1 + {e^{ - {\theta ^T}x}}}}\]损失函数为:\[J(\theta ) =  - \frac{1}{m}\s
logistic回归梯度下降的求导过程
tuoyakan9097的博客
04-22 809
logistic回归梯度下降的求导过程，记录一下
吴恩达老师DeepLearning系列课程最详细学习笔记之20—向量化logistic回归的梯度输出
james9668的博客
05-08 602
教程是本人学习吴恩达老师DeepLearing系列课程中整理的最为详细的学习笔记。学习视频主要来自B站[双语字幕]吴恩达深度学习deeplearning.ai_哔哩哔哩_bilibili?，以及DeepLearning官方网站Deep Learning by deeplearning.ai | Coursera。该系列课程总共有180多个，我会将学习笔记陆续分享出来，为有兴趣深度学习的同仁提供便利。再次由衷感谢吴恩达老师的精彩讲解和无私奉献！ 特别说明：图片来源于吴恩达老师视频截图。 ...
2.9 logistic回归中的梯度下降法
Whiser的博客
04-11 115
Logistic回归和梯度上升算法
whai的专栏
07-08 8148
一. Logistic回归原理Logistic回归是一种广义线性回归，常用的分类器函数是Sigmoid函数，其公式如下： σ(z)=11+e−z\sigma(z)=\frac{1}{1+e^{-z}} 其中，zz可由下面公式得出： z=w0x0+w1x1+w2x2+⋅⋅⋅+wnxnz=w_0x_0+w_1x_1+w_2x_2+\cdot\cdot\cdot+w_nx_n 如果采用向量的写法，
深度学习 实验三 logistic回归预测二分类
渣渣的夏天
05-01 5769
深度学习 实验三 logistic回归预测二分类 学会使用学习到的逻辑回归的知识，手动使用梯度下降方法，通过给定的相关数据来完成年薪是否高于50k的二分类预测任务。
机器学习——Logistic回归
hshagahhva的博客
11-21 1139
一：Logistic回归简介 Logistic回归是统计学习中的经典分类方法，属于对数线性模型，所以也被称为对数几率回归。该模型是一种分类算法，Logistic回归是一种线性分类器，针对的是线性可分问题。我们要了解Logistic回归进行分类的主要思想是：根据现有的数据对分类边界线建立回归方程，然后以此进行分类。这里回归一词源于最佳拟合参数，表示要找到最佳拟合参数集。 Logistic回归的优点在于计算代价不高，易于理解和实现。缺点是容易发生欠拟合现象，分类的精度不高。适...
机器学习——逻辑回归（Logistic Regression）
weixin_74340055的博客
05-28 904
这里，np.ones((X_train.shape[0], 1)) 创建了一个形状为 (n_samples, 1) 的数组，其中 n_samples 是 X_train 的样本数量，所有元素的值都是1。在逻辑回归中，这个函数的主要目的是将线性模型的输出转换为一个介于0和1之间的概率值，这样我们就可以用这个概率值来判断某个样本属于正类（例如，标签为1）的。在逻辑回归中，当我们已经有了线性回归模型的基础后，为了将模型的输出转换为概率值（即预测某个事件发生的可能性），我们引入了sigmoid函数。
【深度学习】1 Logistic回归与梯度下降
weixin_51277640的博客
09-24 328
0 前言 本文是吴恩达教授深度学习课程的个人笔记，细节之处有所遗漏，如想了解更多请参照《神经网络与深度学习》-Stanford吴恩达教授 1 问题的引入 假设我们手边有m张猫的图片，以及一张不知道内容的图片，如何判断这张图片是不是猫呢？或者说，这张图片是猫的概率有多大呢？ 2 分析 我们知道，一张图是由若干像素所组成，每个像素上的颜色是由其RGB值确定，假设这里的照片都是64×64像素，因此，一张照片可以看做红绿蓝三个RGB值组成的64×64矩阵。将这64×64个像素纵向排列，我们就得到了一个64×64维度
logistic算法matlab程序
05-13
基于logistic回归算法的matlab程序实现
【机器学习】逻辑回归（Logistic Regression）模型
Daycym的博客
05-26 1447
写在前面 生活中，常常存在一些分类问题，比如： 垃圾邮件分类 网上交易是否为敲诈 西瓜是好是坏（西瓜书中的例子）等 上述的问题都可以抽象为输出为变量y的问题，前段时间，我通过博客给大家分享了如何使用线性模型进行回归学习，但是若要做的任务是分类问题呢？这里可以考虑广义线性模型：只要找到一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。 考虑二分类任务，其输出标记y∈｛...
图解机器学习-Logistic-学习过程
qq_24059779的博客
09-29 305
针对概率部分的知识稍微回顾一下https://www.jiqizhixin.com/articles/2018-01-09-6  
逻辑回归(Logistic Regression)原理、过程
m0_56051805的博客
12-18 7866
逻辑回归(Logistic Regression)原理、过程
logistic逻辑回归分类算法及应用
xuxu96
04-05 2770
logistic逻辑回归分类算法及应用 3.1 概述 Lineage逻辑回归是一种简单而又效果不错的分类算法。 什么是回归：比如说我们有两类数据，各有50个点组成，当我们把这些点画出来，会有一条线区分这两组数据，我们拟合出这个曲线（因为很有可能是非线性的），就是回归。我们通过大量的数据找出这条线，并拟合出这条线的表达式，再有新数据，我们就以这条线为区分来实现分类。 下图是一个数据集的两组数据，中...
详解逻辑回归（LR）计算过程
热门推荐
这里记录着我一点一滴的进步
08-16 2万+
原文地址：http://blog.csdn.net/dongtingzhizi/article/details/15962797 1.引言 本文主要介绍以下三个方面的内容： （1）Logistic Regression的基本原理，分布在第二章中； （2）Logistic Regression的具体过程，包括：选取预测函数，求解Cost函数和J(θ)，梯度下降法求J(θ)的最小值，以及递归下...
入门学习-------logistic回归及梯度下降算法
wu740027007的博客
07-23 3735
logistic回归 假设现在有一些数据点，需要用一条直线对这些数据点进行拟合，该过程就叫做回归。 logistic回归主要用来解决二分类预测问题，例如判断一张图片是否是猫，一个人是否患有相关疾病等。所以logistic回归的输出值是一个介于0~1之间的概率值。如果用普通的线性函数Y=WX+b，Y的大小是跟随X的变化会线性的增加或缩小，不满足概率值的条件。 所以此时可以借助sigm...
深度学习（2）：logistic回归 梯度下降法
awake020
04-10 1360
二分类问题 我们经常会遇到各种各样的二分类问题，例如判断一张照片是猫或不是猫，判断一个西瓜是好瓜还是坏瓜。解决这类问题的一个很好的方法就是logistic回归。   线性回归 利用简单的线性回归可以进行二分类，这里我们简要介绍以下线性回归的思想，不做具体实现的阐述。 假定拥有的数据集为 m组（x，y）    x 为一组n维列向量，代表我们已知的n个属性    y 为标记，取值为0或1，代表其所属的...
logistic回归分类与softmax回归
奔跑的小仙女
10-21 9459
目录 Logistic回归 逻辑回归的定义式： 损失函数 梯度下降 Logistic回归防止过拟合： Softmax回归： loss函数 逻辑回归与Softmax回归的联系 与神经网络的关系 logistic回归（多分类）和softmax的关系： YOLOV3中的逻辑分类应用 Logistic回归 Logistic回归（LR）：是一种常用的处理二分类问题的模型。 二分类...
logistic回归 和梯度下降
最新发布
03-25
### Logistic 回归与梯度下降的关系 Logistic 回归是一种用于处理二分类问题的监督学习算法，它通过将输入特征的线性组合映射到 0 到 1 的概率范围来进行预测[^1]。然而，在实际应用中，我们需要找到最佳的模型参数以最小化损失函数（通常是交叉熵损失）。这一过程通常依赖于优化技术，其中最常用的方法之一就是梯度下降。 #### 梯度下降的作用 梯度下降是一种迭代优化算法，旨在寻找目标函数的局部极小值。对于 Logistic 回归而言，该目标函数即为损失函数 \( J(\theta) \)，表示模型预测值与真实标签之间的差异程度。通过不断调整权重向量 \( \theta \)，使得损失逐渐减小直至收敛至某个阈值范围内[^4]。 具体来说，每次更新都会沿着负梯度方向移动一定步长（由学习率决定），从而逐步逼近最优解： \[ \theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta) \] 这里，\( \alpha \) 表示学习速率；而偏导数项则反映了当前点处沿各个维度的变化趋势。 #### Python 实现方式 下面展示如何利用 NumPy 库手动编写基于梯度下降法训练逻辑回归模型的核心部分: ```python import numpy as np def sigmoid(z): """Sigmoid 函数定义""" return 1 / (1 + np.exp(-z)) def compute_cost(X, y, theta): """ 计算成本/损失函数 参数: X -- 输入数据矩阵 shape(m,n), m=样本数量 n=特征数目 y -- 输出标签列向量 shape(m,) theta -- 权重参数列向量 shape(n+1,) （含截距） 返回值: cost -- 当前状态下计算得到的成本数值 scalar """ m = len(y) h = sigmoid(np.dot(X, theta)) epsilon = 1e-5 # 防止 log(0) 导致错误 cost = (-1/m)*((np.log(h + epsilon).T @ y)+(np.log(1-h + epsilon).T @(1-y))) return cost.flatten() def gradient_descent(X, y, theta, alpha, num_iters): """ 使用批量梯度下降方法执行参数拟合操作 参数: X -- 扩展后的输入数据矩阵 shape(m,n+1) y -- 输出标签列向量 shape(m,) theta -- 初始化权重参数列向量 shape(n+1,) alpha -- 学习率 float num_iters -- 迭代次数 int 返回值: theta -- 更新后的最终权重参数列向量 shape(n+1,) costs -- 历史记录下的每轮次对应的成本列表 list of floats """ m = len(y) costs = [] for i in range(num_iters): h = sigmoid(np.dot(X, theta)) error = h - y grad = (1/m)*(X.T @ error) theta -= alpha * grad if i % 100 == 0: # 只保存每隔一百次的结果以便绘图观察变化轨迹 current_cost = compute_cost(X, y, theta) costs.append(current_cost) return theta, costs ``` 上述代码片段展示了完整的从零开始构建逻辑回归模型所需的组件，包括激活函数 `sigmoid` 定义、代价函数 `compute_cost` 和核心的学习机制 `gradient_descent` 。值得注意的是，为了简化说明并未加入正则化项或其他改进措施如随机抽样批次等高级特性[^2]^。 ### 总结 通过对理论基础的理解配合编程实战演练可以帮助我们更深刻掌握逻辑回归及其背后的数学本质。借助像 Scikit-Learn 这样的成熟框架固然方便快捷，但从头搭建整个流程同样具有重要意义因为它让我们清楚知道内部运作细节[^3].
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Einstellung

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值