用数学方法算基元碰撞检测 (4)

 

Point In Cylinder

Point  :   P

Cylinder:  |(P – O) - ((P – O) • N) * N | <= R

  0 <= (P – O)• N <= L

 

Structure: { V3d   O;

            float R;

            V3d  N;

            FloatL;  }

                  

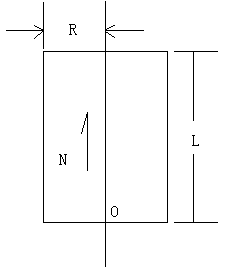
           V = P – O;

           dp = V • N;

           if ( dp < 0 || dp > L )     return Outside;

 

           T = V –dp * N;

 

           if ( T^2 > R^2 )            return Outside;

 

           return Inside;

 

Point In Cone

Point  :   P

Cone   :   |(P – O) – ((P – O) • N) * N| <= ((P – O) • N) * R / L

  0 <= (P – O)• N <= L

 

   The Data Structure of Cone is same as Cylinder.

                        

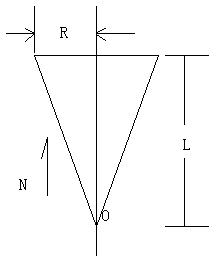
           V = P – O;

           dp = V • N;

           if ( dp < 0 || dp > L )     return Outside;

 

           T = V –dp * N;

 

           r = dp * R / L

          

           if ( T^2 > r^2 )            return Outside;

 

           return Inside;

 

 

Sphere & Cylinder

Sphere :   | P – C | <= r

Cylinder:  |(P – O) - ((P – O) • N) * N | <= R

  0 <= (P – O)• N <= L

 

  OC = C – O;

           dp = OC • N

 

           if ( (dp > L + r) || (dp < -r) )      return No Intersection;

 

           T = OC - dp * N;

 if ( dp > L )

 {

f = sqrt( r^2 – (dp - L)^2 );

if ( T^2 > (R + f)^2 )             return No Intersection;

 

   return Intersectant;

 }

 else if ( dp >= 0 )

 {

if ( T^2 > (R + r)^2 )             return No Intersection;

 

   return Intersectant;

 }

 else

 {

f = sqrt( r^2 – dp^2 );

if ( T^2 > (R + f)^2 )             return No Intersection;

 

   return Intersectant;

 }

 

 

 

Line Segment & Cylinder

Line Seg:  P = P0 + t * V      t ∈ [0, 1]

Cylinder:  |(P – O) - ((P – O) • N) * N | <= R

  0 <= (P – O)• N <= L

 

 OP = P – O = P0 + t * V – O = (P0 – O) + t * V;

           dp = OP • N

           

           dp0 = (P0 – O)• N         t = 0

           if ( dp0 > L )     return No Intersection;

 

           dp1 = (P0 – O + V)• N     t = 1

           if ( dp1 < 0 )     return No Intersection;

 

|(P0 – O) + t * V – (((P0 – O) + t * V) • N) * N | <= R

|(P0 – O) + t * V – ((P0 – O) • N) * N – ((t * V) • N) * N | <= R

|(P0 – O) – ((P0 – O) • N) * N + t * V - t * (V • N) * N | <= R

|((P0 – O) – ((P0 – O) • N) * N) + t * (V - (V • N) * N) | <= R

 

F = (P0 – O) – ((P0 – O) • N) * N;

G = V - (V • N) * N;

 

G^2 * t^2 + 2 * (F • G) * t + F^2 – R^2 = 0;

A = G^2;

B = 2 * (F • G);

C = F^2 – R^2;

 

if ( A > 0 )   //V is not parallel to N

{

          Δ= B^2 – 4AC;

            if ( Δ < 0 )               return No Intersection;

 

          t = (-B ± sqrt(B^2 – 4AC)) / 2A;  

 

          t1 <= t2;

 

          if ( t2 < 0 || t1 > 1 )    return No Intersection;

 

          return Intersectant;

       }

 

if ( C <= 0 )                 return Intersectant;

 

return No Intersection;