一)对PCA协方差的改进
这两天运行着人脸识别的相关程序发现,当数据量一大的时候,比如一个样本集合,随便的就有12*6750等等,在求这个矩阵的协方差与特征向量的时候,按照上一篇的介绍:
使用到里面的Cell_all = PCA(img,k) 函数,会发现一般运行时间都会很久,其实正常在求取大矩阵的协方差特征值与特征向量的时候确实会很麻烦,但是从数学推导上可以发现存在着快速求解的方法。一个变换原理介绍如下:
主成分分析PCA(Principal Component Analysis)介绍在其中的第二点上就是推导变换的过程,这个过程使得求取矩阵的特征向量变快了不少。
正常情况下我们说协方差ST = E{(xi-u)*(xi-u)T} = X'X'T ,它是一个ST是(m*n)*(m*n)阶的矩阵,所以计算它的特征向量比较复杂,但是左如下变换后:
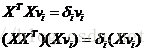
可以看到要计算XTX的特征值和特征向量δi与vi,然后就可以计算出XXT的 特征值和特征向量δi与Xvi,而XTX为N*N阶的矩阵,相比(m*n)*(m*n)阶矩阵来说小不少,计算起来比较容易。
据此我们把以前的PCA程序改为如下:
function [img_new,V] = PCA(img,k)
%reshape函数:改变句矩阵的大小,矩阵的总元素个数不能变
% img = double(img);
% tic;
[m,n] = size(img); %取大小
img_mean = mean(img); %求每列平均值
img_mean_all = repmat(img_mean,m,1);%复制m行平均值至整个矩阵
Z = img - img_mean_all;
T=Z*Z'; %协方差矩阵
[V,D] = eigs(T,k);%计算T中最大的前k个特征值与特征向量
V=Z'*V; %协方差矩阵的特征向量
for i=1:k %特征向量单位化
l=norm(V(:,i));
V(:,i)=V(:,i)/l;
end
img_new = Z*V; %低维度下的各个脸的数据
% toc;相比以前的变化可以看到,主要是对中间的改变了下,以前的程序是这样的:
function [img_new,V] = PCA(img,k)
%reshape函数:改变句矩阵的大小,矩阵的总元素个数不能变
%img = [1,2;2,1;3,3;3,6;6,3];
% k = 2;
% img = double(img);
tic;
[m,n] = size(img); %取大小
img_mean = mean(img); %求每列平均值
img_mean_all = repmat(img_mean,m,1);%复制m行平均值至整个矩阵
Z = img - img_mean_all;
T = Z'*Z;%协方差矩阵
[V,D] = eigs(T,k);%计算T中最大的前k个特征值与特征向量
img_new = Z*V; %低维度下的各个脸的数据
toc;可以看到区别主要在T=Z*Z'; 和T = Z'*Z;以及后面的一点内容,这就是上述原理的部分。为了比较两者性能到底差多少,这里分别使用改与未改的来观察,使用matlab计时器tic与toc如下:
改之前:
>> [img_new,V] = PCA(ImgData,10);
时间已过 3.235867 秒。
改之后:
>> [img_new,V] = PCA(ImgData,10);
时间已过 0.012895 秒。
当后面的10变为50或者100,那么第一种方法求取的时间将会超过100多秒,等不住了。但是这个改变的前提是后面的k=10必须小于矩阵的行与列数,这就带来一个不足,比如如果来个样本集合为12*6750的时候,这个k最大只能是12了,也就是说最大只能降维到12,想在大一些就不可以了,但是第一种情况最大可以降维到6750维。也就是说改进的降维最大数为样本的数量(这里为12)。但是一般样本会很多,应该会超过你需要降维的维数。
会想到这种快速改进的区别是看到一篇不同的博客,研究半天才知道
Matlab PCA+SVM人脸识别(一)
二)关于样本脸的重建
就这上面给的一篇博客中最后一点写到关于如何去重建的原始图像的程序,感觉有点明白且做了下,感觉挺有意思的。
运行人脸识别(二)中的程序
>>ImgData = imgdata();
导入人脸数据,出来ImgData为12*6750的矩阵,运行改进的PCA程序,
>>[img_new,V] = PCA(ImgData,12);
这个时候最大只能降到12维了,不知道够不够,但是样本量就这么多,先这么着看看吧。得到降维后的矩阵与特征向量,假如这里来重建第一副图像,取
Img1 = img_new(1,:);
这里img1就变成了1*12的数列,假设就是[1 2 3 4 5 6 7 8 9 10 11 12];
想想这些数列是怎么来的?比如1就是原始样本矩阵乘以第一主成分特征向量所得,那么重构后就得包括是1*V1,同理重构后的数据也得包括2*V2,等等。
这样就可以把相应位置的数据累加起来就是原始样本在该位置的值。程序与显示如下:
[m,n] = size(ImgData); %取大小
img_mean = mean(ImgData); %求每列平均值 1*6750
for i = 1:12
img_mean = img_mean + img_new(1,i)*V(:,i)';
B=reshape(img_mean,90,75);
subplot(2,6,i);imshow(B,[]);
end运行后的结果为:

照片显示从一次两次一直到12次的重建过程,效果是越来越好吧。























 311
311











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








