2014秋C++第11周项目6参考-回文、素数

课程主页在http://blog.csdn.net/sxhelijian/article/details/39152703，课程资源在云学堂“贺老师课堂”同步展示，使用的帐号请到课程主页中查看。

 

【项目6-回文、素数】
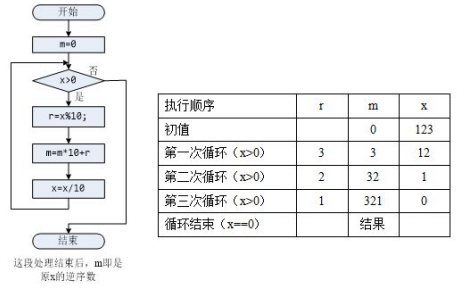
（1）编制一个函数reverse，返回给定数据的“反序数”，例如输入1234，输出4321。请编制reverse函数，在下面代码的基础上补充相关的部分，实现要求的功能。

int main()
{
    int m,n;
    cin>>m;
    n=reverse(m);
    cout<<n<<endl;
}
int reverse(int x)   //函数只管求值，不管输出。输出由main函数完成
{ }

算法提示：流程图及其示例见图。

参考解答：

#include <iostream>
using namespace std;
int reverse(int);//自定义函数的原型（即函数声明）
int main()
{
    int m,n;
    cin>>m;
    n=reverse(m);
    cout<<n<<endl;
}
int reverse(int x)
{
    int m=0;
    while(x>0)
    {
        m=m*10+x%10;
        x=x/10;
    }
    return m;
}

（2）编制isPalindrome()，用于判断参数是否是回文数——回文数，即从前往后读和从后往前读都一样的数，如1221和121都是回文数，而1231、123都不是回文数。请编制isPalindrome(函数，在下面代码的基础上补充相关的部分，实现要求的功能。

int main()
{
    int m;
    cin>>m;
    if(isPalindrome(m))
        cout<<m<<"是回文数，噢耶！"<<endl;
    else
        cout<<m<<"不是回文数。回文有什么好！"<<endl;
    return 0;
}

bool isPalindrome(int n)
{ }

参考解答1：

#include <iostream>
using namespace std;
bool isPalindrome(int);//自定义函数的原型（即函数声明）
int main()
{
    int m;
    cin>>m;
    if(isPalindrome(m))
        cout<<m<<"是回文数，噢耶！"<<endl;
    else
        cout<<m<<"不是回文数。回文有什么好！"<<endl;
    return 0;
}
 
bool isPalindrome(int n)
{
    bool palindrome=false; //先默认不是回文数
    int m,k;
    m=n;
    k=0;//k用于求出n的反序数
    while(m>0)
    {
        k=k*10+m%10;
        m=m/10;
    }
    if(k==n)
        palindrome=true;
    return palindrome;
}

参考解答2：这样划分功能更合适

#include <iostream>
using namespace std;
bool isPalindrome(int);//自定义函数的原型（即函数声明）
int reverse(int);
int main()
{
    int m;
    cin>>m;
    if(isPalindrome(m))
        cout<<m<<"是回文数，噢耶！"<<endl;
    else
        cout<<m<<"不是回文数。回文有什么好！"<<endl;
    return 0;
}
 
bool isPalindrome(int n)
{
    bool palindrome=false; //先默认不是回文数
    if(reverse(n)==n)
        palindrome=true;
    return palindrome;
}
 
int reverse(int x)
{
    int m=0;
    while(x>0)
    {
        m=m*10+x%10;
        x=x/10;
    }
    return m;
}

（3）编制一个返回值为bool型的函数isPrimer()，用于判断参数是否为素数（是素数返回true，否则false），自编main函数用于测试；

int main()
{
    //此处写代码，能够调用isPrimer函数完成“测试”
}

bool isPrimer(int n)  //在这个函数中只管判断，不能出现cout语句！
{
}

参考解答：

#include<iostream>
#include<cmath>
using namespace std;
bool isPrime(int);
int main()
{
    int m;
    cin>>m;
    cout<<m<<((isPrime(m))?"是":"不是")<<"素数。"<<endl;
    return 0;
}
 
bool isPrime(int n)
{
    bool prime=true;
    int k=int(sqrt(n));
    for(int i=2;i<=k;i++)
    {
        if(n%i==0)
        {
            prime=false;
            break;
        }
    }
    return prime;
}

（4）编制main函数，调用上面定义的3个函数，完成
输出1000以内的所有素数。
输出1000以内的所有回文数。
输出1000以内的所有回文素数。

若一个素数的反序数仍为素数，则称它为可逆素数。求10000以内的所有可逆素数。

参考解答：

#include<iostream>
#include<cmath>
using namespace std;
bool isPalindrome(int);//自定义函数的原型（即函数声明）
int reverse(int);
bool isPrime(int);
int main()
{
    int m;
    cout<<"（1）输出1000以内的所有素数"<<endl;
    for(m=2;m<1000;++m)
    {
        if(isPrime(m))
            cout<<m<<'\t';
    }
    cout<<endl<<endl;
    cout<<"（2）输出1000以内的所有回文数"<<endl;
    for(m=2;m<1000;++m)
    {
        if(isPalindrome(m))
            cout<<m<<'\t';
    }
    cout<<endl<<endl;
    cout<<"（3）输出1000以内的所有回文素数"<<endl;
    for(m=2;m<1000;++m)
    {
        if(isPalindrome(m)&&isPrime(m))
            cout<<m<<'\t';
    }
    cout<<endl<<endl;
    cout<<"（4）求1000以内的所有可逆素数"<<endl;
    for(m=2;m<1000;++m)
    {
        if(isPrime(m)&&isPrime(reverse(m)))
            cout<<m<<'\t';
    }
    return 0;
}
 
bool isPrime(int n)
{
    bool prime=true;
    int k=int(sqrt(n));
    for(int i=2;i<=k;i++)
    {
        if(n%i==0)
        {
            prime=false;
            break;
        }
    }
    return prime;
}
 
bool isPalindrome(int n)
{
    bool palindrome=false; //先默认不是回文数
    if(reverse(n)==n)
        palindrome=true;
    return palindrome;
}
 
int reverse(int x)
{
    int m=0;
    while(x>0)
    {
        m=m*10+x%10;
        x=x/10;
    }
    return m;
}

（5）将上面自定义的3个函数放到一个cpp文件中，而将main()函数放在另外一个cpp文件中，改造上面的工作，用多文件的方式组织程序。

（略）

=================== 迂者 贺利坚 CSDN博客专栏================= |==　IT学子成长指导专栏　专栏文章的分类目录（不定期更新）　==| |==　C++ 课堂在线专栏　　贺利坚课程教学链接（分课程年级）　==| |==　我写的书——《逆袭大学——传给IT学子的正能量》　　　　==| ===== 为IT菜鸟起飞铺跑道，和学生一起享受快乐和激情的大学 =====