连续函数有一个重要的性质,那就是当
x
靠近
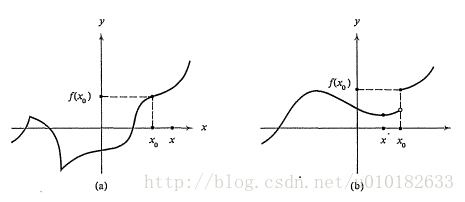
图1
为了精确地定义连续,首先需要定义函数在一个点处的极限概念。
定义1
令
A⊂Rn,f:A→Rm
,假设
x0
是
A
的一个聚点,我们说
如果给定任意的 ε>0 ,存在 δ>0 (依赖于 f,x0,ε )使得对所有的 x∈A,x≠x0 , ∥x−x0∥<δ 意味着 ∥f(x)−b∥<ε 。
直观上讲就是当
x
靠近
注意极限 limx→x0f(x) 可能不存在;例如,令 f:R∖{0}→R 定义为如果 x<0,f(x)=1 ,如果 x>0,f(x)=2 ,那么0是 R∖{0} 的聚点但是 limx→0f(x) 不存在。然而,如果 x≠0 时, f(x)=1 ,并且 f(0)=0 ,那么 limx→0f(x)=1 。另一个例子是 f:R∖{0}→R,f(x)=sin(1/x) ;这个函数越靠近0振荡越快,所以不会靠近任何极限。然而,如果 limx→x0f(x) 存在,那么它是唯一的。假设 limx→x0f(x)=b,b′ ,为了说明 b=b′ ,令 ε>0 ,那么存在 δ1>0,δ2>0 使得 ∥x−x0∥<δ1 意味着 ∥f(x)−b∥<ε/2 , ∥x−x0∥<δ2 意味着 ∥f(x)−b′∥ε/2 ,令 δ=min{δ1,δ2} ;那么 ∥x−x0∥<δ 意味着 ∥b−b′∥≤∥b−f(x)∥+∥f(x)−b′∥<ε/2+ε/2=ε ;因此对任意 ε,∥b−b′∥<ε ,所以 ∥b−b′∥=0 或者 b=b′ 。
接下来我们开始定义函数在一点处连续的概念。
定义2
令
A⊂Rn,f:A→Rm,x0∈A
。我们说
f
在
注意除了极限
这里介绍有用的符号。假设
f
在
意味着
f
在定义域
为
x
从左边靠近
定义3
函数
f:A→Rm
在集合
B⊂A
上连续,如果
f
在
还有许多其他的方式来形式化连续的概念,其中有一个非常重要,因为它只涉及到拓扑学(也就是开集),所以它应用更广。
-
f
在
A 上连续 - 对于
A
中的每个收敛序列
xk→x0 ,我们有 f(xk)→f(x0) - 对于
Rm
中的每个开集
U
,
f−1(U)⊂A 对 A 而言是相对开的;即,对某个开集V,f−1(U)=V∩A - 对于每个闭集
F⊂Rm,f−1(F)⊂A
对
A
而言是相对闭的;即,对某个闭集
G,f−1(F)=G∩A
实际上,定理中的
(ii)
与极限有类似的版本,即如果
f:A→Rm
并且
x0
是
A
的聚点,那么
当且仅当对于每个收敛到
x0
的序列
xk∈A
,
从定理中可以看出,前面文章中提到的连续路径与这里定义的连续是一致的。之后的文章会介绍一些定理,根据这些定理我们就可以很容易的建立一般函数的连续性。
现在我们简要讨论一下定理1。首先,
(i)
与
(ii)
的等价性比较明显,因为
(i)
意味着
x
靠近
现在我们看一下
(iii)
告诉了我们什么,选择一个小的开集
U
,它包含
例1: 令 f:Rn→Rn 是单位函数 x↦x ,说明 f 是连续的。
如果
|x−x0|<δ
,那么我们将得到
接下里,如果我们令
δ<x0/2
,那么我们将得到
x>x0/2
(图
???
),所以
δ/xx0<(2δ/x20)
。现在给定
ε>0
,选择
δ=min(x0/2,εx20/2)
,那么
f
在
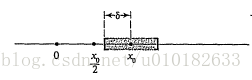
图2
例3: 令 f:Rn→Rm 是连续的,说明 {x∈Rn|∥f(x)∥<1} 是开的。
解: 上面的集合实际上就是 f−1{y|∥y∥<1} ,它是一个开集的逆像,根据定理1 (iii) 可知它是开集。





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








