005四元数与姿态阵间的关系

---

学习惯导这么久，还是没有形成自己的体系，应该说还是没有入门（手动尴尬）。所以在此对看过的内容进行解释，加深印象。本文的内容针对秦永元老师《惯性导航（第二版）》中“9.2.2 四元数与姿态阵间的关系”进行备忘。

一、前提

如图所示（为了便于理解，我把原图擦去了一部分），假定有刚体金刚圈AB，坐标系R，注意这个坐标系不与金刚圈固联（无论金刚圈怎么转，我坐标系坚决不动，相当于这是一个导航坐标系）。当看到这个图，你肯定不知道坐标系R在哪了。没关系，这都不重要，可以这么认为，坐标系就假定是以O为原点的右手系（O隐藏的很深，仔细看）。

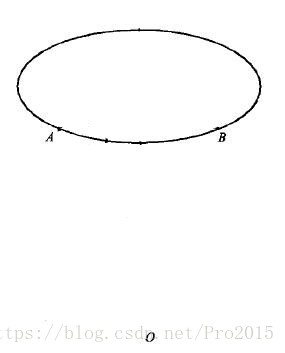
金刚圈跟坐标系R介绍完了，就该谈一谈其中的元素了。请看下面这个被我蹂躏得比较轻的图。连接OO’（O’为圆心）得矢量$\overrightarrow{O{O}^{\prime }}$，连接O’A得矢量$\overrightarrow{O’A}$，连接O’B得矢量$\overrightarrow{O^{\prime }B}$（$\overrightarrow{O^{\prime }A}$垂直于$\overrightarrow{O^{\prime }B}$），连接OA得矢量$\overrightarrow{OA}$记为$\vec{r}$。把这些元素定义好了，金刚圈就开始绕$\overrightarrow{O{O}^{\prime }}$转动，转动方向沿短弧沿短弧$A\stackrel{沿短弧}{\to }B$。

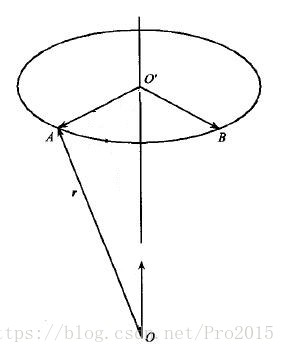
圆圈的转动还是要作一下说明，如下图所示（这个图没有遭到我的毒手）。在$\overrightarrow{OO}$上取单位矢量$\vec{u}$，该矢量可以等效成刚体的旋转轴。$\overrightarrow{O^{\prime }A}$旋转角度$\theta$得到$\overrightarrow{O^{\prime }{A}^{\prime }}$，连接OA’得到$\overrightarrow{O{A}^{\prime }}$记为${\vec{r}}^{\prime }$。

到此为止，把旋转的关系理清楚了。下面请看四元数与姿态阵关系的推导过程。

二、推导

推导的过程其实就是分析转动前后的矢量$\vec{r}$与${\vec{r}}^{\prime }$的关系。

根据前面的描述，首先可以得到：
$$\overrightarrow{O{O}^{\prime }}=(\vec{r}\cdot \vec{u})\vec{u}$$

为什么呢？因为：
$$\begin{gathered} \overrightarrow{O{O}^{\prime }}=(|\vec{r}|\cdot |\vec{u}|\cdot cos<\vec{r},\vec{u}>)\vec{u} \\ =|\overrightarrow{O{O}^{\prime }}|\cdot \vec{u}=\overrightarrow{O{O}^{\prime }} \end{gathered}$$

那么可求：
$$\overrightarrow{O^{\prime }A}=\vec{r}-\overrightarrow{O{O}^{\prime }}=\vec{r}-(\vec{r}\cdot \vec{u})\vec{u}$$

$$\begin{gathered} \overrightarrow{O^{\prime }B}=\vec{u}\times \overrightarrow{O^{\prime }A} \\ =\vec{u}\times \vec{r}-\vec{u}\times (\vec{r}\cdot \vec{u})\vec{u} \\ =\vec{u}\times \vec{r}-(\vec{r}\cdot \vec{u})\vec{u}\times \vec{u} \\ =\vec{u}\times \vec{r} \end{gathered}$$

这一步，点乘是一个实数，所以会有$\vec{u}\times \vec{u}$，而$\vec{u}\times \vec{u}=0$。

说到这里又要再加一个图了，如下图，这个图的意思不用我多说了吧。

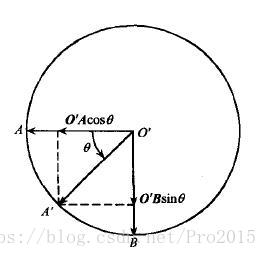
通过这个图求$\overrightarrow{O^{\prime }{A}^{\prime }}$:
$$\begin{gathered} \overrightarrow{O^{\prime }{A}^{\prime }}=\overrightarrow{O^{\prime }A}cos\theta +\overrightarrow{O^{\prime }B}sin\theta \\ =\vec{r}cos\theta -(\vec{r}\cdot \vec{u})\vec{u}cos\theta +\vec{u}\times \vec{r}sin\theta \end{gathered}$$
这样，${\vec{r}}^{\prime }$就可以求得：
$$\begin{gathered} {\vec{r}}^{\prime }=\overrightarrow{O{O}^{\prime }}+\overrightarrow{O^{\prime }{A}^{\prime }} \\ =\vec{r}cos\theta +(1-cos\theta )(\vec{r}\cdot \vec{u})\vec{u}+\vec{u}\times \vec{r}sin\theta \end{gathered}$$

另外有这样一个公式，在推导的过程中需要用到（公式来源：向量积-拉格朗日公式）：
$$\vec{a}\times (\vec{b}\times \vec{c})=\vec{b}(\vec{a}\cdot \vec{c})-\vec{c}(\vec{a}\cdot \vec{b})$$
我们知道向量的点乘满足交换律，所以可以写成：
$$\vec{a}\times (\vec{b}\times \vec{c})=\vec{b}(\vec{a}\cdot \vec{c})-(\vec{a}\cdot \vec{b})\vec{c}$$
这时候令$\vec{a}=\vec{b}=\vec{u}$，$\vec{c}=\vec{r}$，可得：
$$\vec{u}\times (\vec{u}\times \vec{r})=\vec{u}(\vec{u}\cdot \vec{r})-(\vec{u}\cdot \vec{u})\vec{r}$$
现在就跟书上的对照起来啦。接下来还有$\vec{u}\cdot \vec{u}=1$，所以上式可表示为：
$$\begin{gathered} \vec{u}\times (\vec{u}\times \vec{r})=\vec{u}(\vec{u}\cdot \vec{r})-\vec{r} \\ =(\vec{r}\cdot \vec{u})\vec{u}-\vec{r} \end{gathered}$$
所以可以得到：
$$(\vec{r}\cdot \vec{u})\vec{u}=\vec{r}+\vec{u}\times (\vec{u}\times \vec{r})$$
够详细了吧，我这颗心那，就怕以后看不懂！！

所以可以得到：
$$\begin{gathered} {\vec{r}}^{\prime }=\overrightarrow{O{O}^{\prime }}+\overrightarrow{O^{\prime }{A}^{\prime }}=\vec{r}cos\theta +(1-cos\theta )(\vec{r}\cdot \vec{u})\vec{u}+\vec{u}\times \vec{r}sin\theta \\ =\vec{r}cos\theta +(1-cos\theta )[\vec{r}+\vec{u}\times (\vec{u}\times \vec{r})]+\vec{u}\times \vec{r}sin\theta \\ =\vec{r}+\vec{u}\times \vec{r}sin\theta +(1-cos\theta )\vec{u}\times (\vec{u}\times \vec{r}) \end{gathered}$$
下面就是将${\vec{r}}^{\prime }$向R系内投影，表示为：
$${\vec{r}}^{\prime R}={\vec{r}}^R+(\vec{u}\times \vec{r}{)}^{R}sin\theta +(1-cos\theta )[\vec{u}\times (\vec{u}\times \vec{r}){]}^R$$
记
$${\vec{r}}^{\prime R}=\left[\begin{array}{c}{r}_x^{\prime }\\ r_y^{\prime }\\ r_z^{\prime }\end{array}\right],{\vec{r}}^R=\left[\begin{array}{c}{r}_x\\ r_y\\ r_z\end{array}\right],{\vec{u}}^R=\left[\begin{array}{c}l\\ m\\ n\end{array}\right]$$

看到这肯定又不懂了。其实就是将转动后得到的$\overrightarrow{O{A}^{\prime }}$投影到原来的R系中，然后在R系内将投影的向量用坐标表示出来了。

此时根据叉乘表达式可以得到：
$$(\vec{u}\times \vec{r}{)}^R=\left[\begin{array}{ccc}0& -n& m\\ n& 0& -l\\ -m& l& 0\end{array}\right]\left[\begin{array}{c}{\vec{r}}_x\\ {\vec{r}}_y\\ {\vec{r}}_z\end{array}\right]$$
记
$$U=\left[\begin{array}{ccc}0& -n& m\\ n& 0& -l\\ -m& l& 0\end{array}\right]\text{\hspace{1em}(1)}$$

这又是什么鬼？不要慌，下面来拓展反对称阵。
设
$$\vec{a}=\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right],\vec{b}=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]$$
$$\vec{a}\times \vec{b}=\left|\begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|=\left[\begin{array}{c}{a}_2{b}_3-a_3{b}_2\\ a_3{b}_1-a_1{b}_3\\ a_1{b}_2-a_2{b}_1\end{array}\right]$$
而
$$\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]=\left[\begin{array}{c}{a}_2{b}_3-a_3{b}_2\\ a_3{b}_1-a_1{b}_3\\ a_1{b}_2-a_2{b}_1\end{array}\right]$$
则记
$$(a\times )=\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]，\vec{a}\times \vec{b}=(a\times )\vec{b}$$

因此可以继续往下推导：
$$(\vec{u}\times \vec{r}{)}^R=U{\vec{r}}^R,[\vec{u}\times (\vec{u}\times \vec{r}){]}^R=U\cdot U{\vec{r}}^R$$
所以：
$$\begin{gathered} {\vec{r}}^{\prime R}={\vec{r}}^R+(\vec{u}\times \vec{r}{)}^{R}sin\theta +(1-cos\theta )[\vec{u}\times (\vec{u}\times \vec{r}){]}^R \\ ={\vec{r}}^R+U{\vec{r}}^{R}sin\theta +(1-cos\theta )U\cdot U{\vec{r}}^R \\ =(I+2Usin\frac{\theta }{2}cos\frac{\theta }{2}+2si{n}^2\frac{\theta }{2}U\cdot U){\vec{r}}^R\text{\hspace{1em}(2)} \end{gathered}$$
令：
$$D=I+2Usin\frac{\theta }{2}cos\frac{\theta }{2}+2si{n}^2\frac{\theta }{2}U\cdot U\text{\hspace{1em}(3)}$$
那么
$${\vec{r}}^{\prime R}=D{\vec{r}}^R\text{\hspace{1em}(4)}$$
之后的关系递推比较简单，假定刚体的固联坐标系为$b_0$，刚体未转动时，刚体固联坐标系与参考坐标系R重合，就是对向量$\vec{r}$（注意，这是刚体没有转动的向量）而言，在两个坐标系中的矢量是相等的：
$${\vec{r}}^R={\vec{r}}^{b_0}$$
在刚体转动后，因为向量$\vec{r}$与坐标系$b_0$都随着刚体一起转动，转动结束后得到向量$\vec{r}$和坐标系b。向量${\vec{r}}^{\prime }$可以说相对于坐标系b没动：
$${\vec{r}}^{b_0}=\vec{r}{’}^b$$
所以：
$${\vec{r}}^R=\vec{r}{’}^b$$
带入（4）可得：
$${\vec{r}}^{\prime R}=D{\vec{r}}^{\prime b}$$
那么b系到R系的旋转矩阵即为D:
$$C_b^R=D=I+2Usin\frac{\theta }{2}cos\frac{\theta }{2}+2si{n}^2\frac{\theta }{2}U\cdot U$$
后面的展开用四元数表示就不再赘述，但在此列出：

定义：
$$\begin{gathered} q_0=cos\frac{\theta }{2} \\ {q}_1=lsin\frac{\theta }{2} \\ {q}_2=msin\frac{\theta }{2} \\ {q}_3=nsin\frac{\theta }{2} \end{gathered}$$
有：
$$C_b^R=\left[\begin{array}{ccc}{q}_0^2+q_1^2-q_2^2-q_3^2& 2(q_1{q}_2-q_0{q}_3)& 2(q_1{q}_3+q_0{q}_2)\\ 2(q_1{q}_2+q_0{q}_3)& q_0^2-q_1^2+q_2^2-q_3^2& 2(q_2{q}_3-q_0{q}_1)\\ 2(q_1{q}_3-q_0{q}_2)& 2(q_2{q}_3+q_0{q}_1)& q_0^2-q_1^2-q_2^2+q_3^2\end{array}\right]$$

---

###资源：
秦永元-惯性导航-资源汇总页中下载
学术不需要积分！