转自:http://www.csdn123.com/html/mycsdn20140110/f9/f9f203e02a7cc4b223884ca805d75eab.html
本征矩阵E:它包含了物理空间中两个摄像机相关的旋转(R)和平移信息(T)。T和R描述了一台摄像机相对于另外一台摄像机在全局坐标系中的相对位置。
基础矩阵F:除了包含E的信息外,还包含了两个摄像机的内参数。由于F包含了这些内参数,因此它可以在像素坐标系将两个摄像机关联起来。
OpenCV中文版书中给出了本征矩阵E和基础矩阵F之间区别的解释:
本征矩阵E,是单几何意义上的,与成像仪无关,它将左摄像机观测到的点P的物理坐标和右摄像机观测到的相同的点的位置关联起来(例如将pl和pr关联)。
基础矩阵F,则是将一台摄像机的像平面上的点在图像坐标(像素)上的坐标和另一台摄像机的像平面上的点关联起来(在这里我们标定为ql,和qr)。
以下是个人对上面话的理解,不免出现理解错误,随着后面知识的配合理解,如错了会及时回来修正。
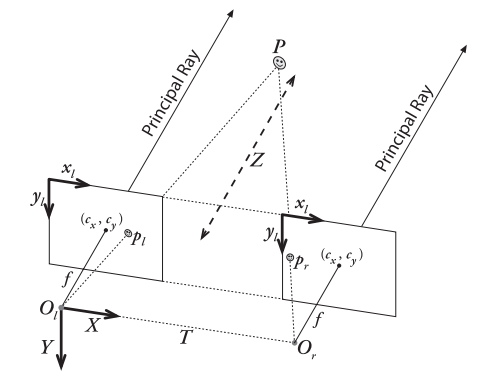
为了方便理解我们引入下图:
1、对于本征矩阵,如上图,对于左相机系我们选用OlXYZ为左摄像机坐标系(其中投影中心Ol为原点,Z轴为光轴的方向),同样的对于右相机,我们采用同样的方法建立右摄像机坐标系。那么上图中点pl和pr分别相对于各自的摄像机有各自的坐标,我们不妨设为pl(x1,y1,z1),pr(x2,y2,z2)。那么回到上面的内容,此时pl和pr就是对应上面黄色的pl和pr。
2、对于基础矩阵,如上图,我们对于左图像我们选择xlyl为图像坐标系,对于右相机也选择右上角为原点的图像坐标系,那么点pl和pr相对于图像坐标系的坐标。我们不妨设为pl(x,y),pr(x0,y0),此时对应上面黄色的的ql和qr坐标。
本征矩阵数学
在这里我首先说明一下pl,pr和Pl,Pr的区别:
1、pl,pr表示P在两个成像仪上所成的像在左右两个摄像机坐标系下的坐标。
2、P1,Pr表示点P在左右两个摄像机坐标系下的坐标。
给定点P,我们将要推导点P在两个成像仪的观测位置pl和pr之间的关系,pl和pr是在两个摄像机坐标系中观察到的点的物理坐标。利用对极几何可以将它们联系起来。
我们知道点Pl是点P在左摄像机Ol为中心的坐标系下的坐标。Pr是P点在右摄像机Or为中心的坐标系下的坐标。
我们令左摄像机Ol为坐标系的中心,Or相对于Ol的坐标为T,R表示旋转矩阵,那么Pr=R(Pl-T)。
Pr为3×1的列向量(相对于中心点),R为3×3的旋转矩阵,P1为3×1的列向量,T也是3×1的列向量。(因为Pr,Pl,T都是三维点)。
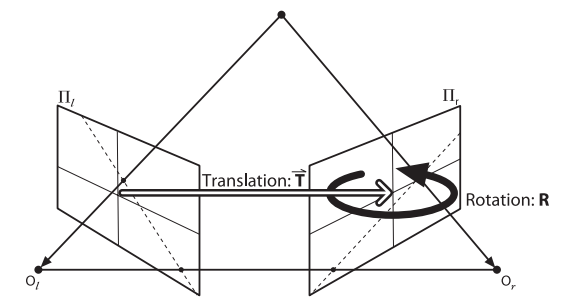
OpenCV书中给出了如下的一副图:
公式Pr=R(Pl-T),Pl表示在以Ol为原点的坐标,Pr表示以Or为原点的坐标。T=目标原点-摄像机原点。那么如果右摄像机的原点为T,那么就相当于右摄像机为“目标原点”,左摄像机为“摄像机原点”,这就和旋转矩阵和平移向量部分相吻合。
关键的一步是引入极面,它联系所有的相关事务。
我们知道描述一个空间平面可以用点法式来确定即平面的法向量和平面上的所有点x表示如下:
a表示平面内的一个定点,x表示平面内的任意一点,n是该平面的法向量。(上面a,x,n每一个都是一个向量,中间是点积)
我们选取左摄像机的投影中心Ol为坐标系的中心,即Ol为原点(0,0,0),那么点Pl和点T,就可以表示为相对于Ol的向量。那么极面上就有向量Pl和T,我们知道右手准则,与P1和T相垂直的向量和法向量同相,并且为P1和T的叉乘。那么通过点T的所有可能点Pl,以及包含这两个向量的方程表示如下:
将公式Pr=R(Pl-T) 即Pl-T=R-1Pr,并且R-1=RT(R是正交阵)得:
总是可以将叉积写成矩阵相乘的形式,故定义矩阵S为:
这样就推导出了第一个结果,将上式带入到叉积公式中,得到:
乘积RS就是我们的定义的本征矩阵,我们可以写成下面的简洁形式:
上述公式给出了点P在两个坐标系下的坐标之间的关系,但是我们要求解的是点P在两个成像仪上的投影点在两个坐标系下的关系。那么,我们利用投影方程(几何关系)即:
将上述两个投影方程带入到上面的公式,并且除以ZlZr/flfr,得到最终的公式:
总结:
1、E是一个秩亏矩阵,即为一个秩为2的3×3矩阵,因此方程实际上有无穷个解。例如,我们已知点pr和本征矩阵E,求解pl,那么我们求解不为唯一的pl。(或许是一条直线)。
2、本征矩阵中共有7个约束,即三个旋转参数、两个平移参数(没有设置缩放?)以及两个其他约束。
两个其他约束:
1)行列式值等于0(秩为2的3阶方阵)
2)两个非零奇异值相等(SVD分解),因为S是反对称阵,而R是旋转矩阵。
3、E不包括摄像机的内参数,因此它联系的是点的物理坐标或者摄像机坐标而不是像素坐标。
基础矩阵数学
本征矩阵E包含两台摄像机相关的所有几何信息,但不包括摄像机本身的任何信息。
在实际应用中,我们通常只对像素坐标感兴趣。为了将像素坐标和极线联系起来,即必须将两台摄像机的内参入信息引入进来,在相机标定——基本几何投影知识中讲到:
即相机内参数将相机坐标系下的坐标和图像坐标系下的坐标关联起来。
我们用p(像素坐标)代替本征矩阵公式中的q,已知q=Mp,即p=M-1q,那么关于本征矩阵E的公式变为:
我们定义基础矩阵F为:
因此有:
总结:
1、我们观察摄像机内参数矩阵M,如果图像没有畸变,即cx,cy为0,并且焦距进行了归一化处理,那么M就成了单位阵,此时本征矩阵F就等于基础矩阵E,即F=E。
2、基础矩阵F的秩也是2。
3、基础矩阵F有七个参数,其中两个参数是对级,三个参数表示两个像平面的单应性矩阵。(这方面可能需要后续知识配合理解)。





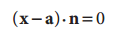
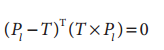
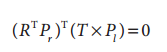
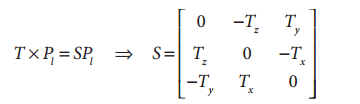
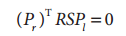
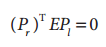
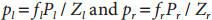
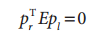
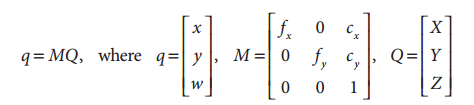
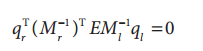
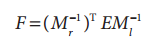
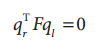
















 6245
6245

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








