微积分3 复习 （无穷级数）比较审敛法,比值审敛法,根值审敛法,积分审敛法,绝对收敛和条件收敛,收敛区间,收敛域,收敛半径,幂级数求和,幂级数展开,一致收敛性,傅里叶级数

1,审敛:

基础知识:

两个常见的级数

1,(q在n下)等比级数： ∑ a*q^n

        对于这种级数，当q>=1的时候发散，当q<1的时候收敛

2,(p在n上)p级数          ∑ n^(-p)

        对于这种级数,当p>1的时候收敛,当p<1的时候发散,当p==1的时候需要我们人为的去讨论

方法:

1,比较审敛法

(通过放缩来实现判断收敛性的判断)       (对于正向级数)

eg:   

主要思想是先预测下究竟是发散还是收敛,

如果预测是收敛,就找一个比原式大但是收敛的式子

如果预测是发散,就找一个比原式小但是发散的式子

比如上题,当n->∞时,1/n为0,所以求和符号内部一定会趋于0,那么我们就预测时收敛的,就开始找一个更大但是收敛的式子来将不好运算的部分消去,方便我们运算

2,比值法/根值法判断敛散性

(对于正向级数)

假设级数时Un, t=Un/U(n+1) = (Un)^(1/n)

当t>1时,级数发散,当t<1时,级数收敛,当t==1时需要讨论

eg:

3,积分审敛法

(对于正向级数):正向级数的发散和收敛与其的积分形式一致

eg:

\

4,牛顿莱布尼兹判别法

(对于交错级数)(-1)^n*Un

当Un单调递减且当n->∞时,Un=0,则有原级数收敛

eg: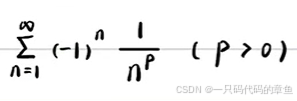

5,绝对收敛和条件收敛

绝对收敛:∑|Un|收敛叫做绝对收敛,如果绝对收敛,原级数也一定收敛

条件收敛:∑|Un|收敛发散,但是∑Un收敛叫做条件收敛

eg:证明绝对收敛,则原级数收敛

2,收敛区间/域/半径

收敛半径 :1/t

收敛区间不包括端点,但是收敛域要去研究端点

eg:

我们让y=x-1,将x=-1带入,发现级数在y=-2处收敛,所以在|y|<=2的区间内都是收敛的,所以当x=2,y=1时,级数绝对收敛

 

 

 3,级数求和

就是利用等比数列的求和公式和求和符号可以和求导/积分符号换位置来做

1,积分with求和

2,导数with求和

如果是多项式的形式,可以将其拆开来运算

4.幂级数展开

就是利用泰勒公式or求导后积分来帮助我们完成

常用1/(1+x) = ∑(-1)^n * x^n

        1/(1-x)= ∑x^n

5,函数项级数的一致收敛性以及其和函数的连续性

判别法:

柯西收敛准则

eg:

M判别法:

只有当级数一致收敛,其和函数才有连续性

6,傅里叶级数

拟合周期函数的

迪利克雷定理

周期延拓和正余弦函数

上面是奇延拓后的余弦级数下面是偶延拓的正弦级数

周期是2l