基于MATLAB 并联机器人 Stewart 并联平台仿真运动学逆解并联机器人运动学、动力学、算法、三维仿真 Matlab Simulink simscape

资深码侬

于 2025-02-28 09:29:44 发布

阅读量892

点赞数 28

分类专栏： MATLAB-仿真模型文章标签： matlab 机器人算法

本文链接：https://blog.csdn.net/2501_90314346/article/details/145919551

版权

MATLAB-仿真模型专栏收录该内容

80 篇文章

订阅专栏

基于MATLAB 并联机器人 Stewart 并联平台仿真运动学逆解并联机器人运动学、动力学、算法、三维仿真 Matlab Simulink simscape
在这里插入图片描述

Stewart平台是一种六自由度的并联机器人，它由一个固定平台和一个移动平台组成，通过六个线性执行器（或称为作动器）连接。这种类型的机器人广泛应用于飞行模拟器、精密加工设备等领域。在MATLAB/Simulink中实现Stewart平台的仿真涉及运动学逆解、动力学分析以及三维可视化。

1. 运动学逆解

1.1 基本原理

Stewart平台的运动学逆解是指根据给定的移动平台的位置和姿态，计算出六个作动器的长度。这通常涉及到坐标变换和非线性方程组的求解。

1.2 MATLAB代码示例

以下是一个简化的运动学逆解的MATLAB代码示例：

function actuator_lengths = inverseKinematics(platform_position, platform_orientation)
    % 定义固定平台和移动平台上的点
    fixed_points = [0 0 0; 1 0 0; 0 1 0; -1 0 0; 0 -1 0]; % 固定平台上的点（简化）
    moving_points = [0 0 1; 1 0 1; 0 1 1; -1 0 1; 0 -1 1]; % 移动平台上的点（简化）

    % 应用平台位置和平移
    R = eul2rotm(platform_orientation); % 旋转矩阵
    T = trvec2tform(platform_position); % 平移向量转换为变换矩阵

    % 计算每个作动器的长度
    actuator_lengths = zeros(size(fixed_points, 1), 1);
    for i = 1:size(fixed_points, 1)
        % 将移动平台上的点转换到全局坐标系
        global_moving_point = T * (R * moving_points(i, :)');
        % 计算作动器长度
        actuator_lengths(i) = norm(global_moving_point - fixed_points(i, :)');
    end
end

注意：上述代码是高度简化的，实际应用中需要考虑更复杂的几何关系和数学模型。

2. 动力学分析

对于动力学分析，可以使用MATLAB的Simscape Multibody工具箱来建立物理模型，并进行动力学仿真。以下是创建Stewart平台的基本步骤：

打开Simulink，创建一个新的Simscape Multibody项目。
导入或创建Stewart平台的3D模型。如果已有STL文件，可以直接导入；否则，可以在SolidWorks等软件中设计后导入。
添加关节和作动器。为每个作动器添加Prismatic Joint（平移关节），并设置相应的控制信号。
定义输入输出接口。包括平台位置和姿态的输入，以及各作动器长度的输出。

3. 算法与控制

PID控制器：用于控制每个作动器的伸缩，以实现期望的平台位置和姿态。
轨迹规划：生成平滑的轨迹，确保平台从初始位置平稳过渡到目标位置。

4. 三维仿真

利用MATLAB的plot3函数或者更高级的图形库如plotly，可以实现Stewart平台的三维可视化。下面是一个简单的例子：

% 示例数据
fixed_points = rand(6, 3); % 固定点位置
moving_points = rand(6, 3); % 移动点位置

% 绘制Stewart平台
figure;
hold on;
for i = 1:6
    plot3([fixed_points(i, 1), moving_points(i, 1)], ...
          [fixed_points(i, 2), moving_points(i, 2)], ...
          [fixed_points(i, 3), moving_points(i, 3)], 'r-', 'LineWidth', 2);
end
axis equal;
grid on;
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Stewart Platform Visualization');

总结

以上提供了基于MATLAB/Simulink对Stewart并联平台进行运动学逆解、动力学分析及三维仿真的基本方法和部分代码示例。实际操作时，需根据具体需求调整参数和算法。希望这些信息对你有所帮助！
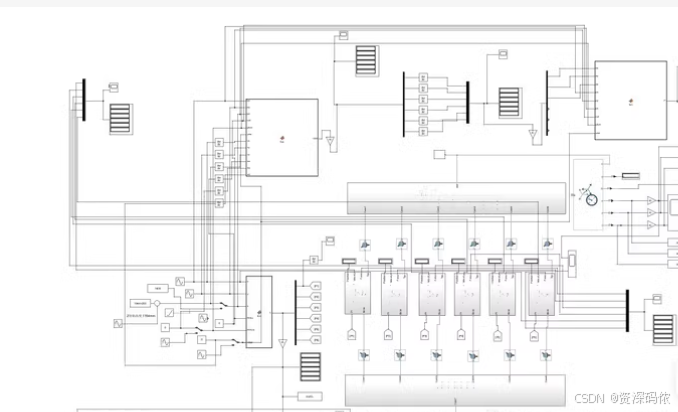
在这里插入图片描述
这张图片展示了一个在MATLAB Simulink中构建的Stewart平台仿真模型。为了更好地理解和使用这个模型，我将提供一个详细的解释，并附上相关的代码和说明。

1. 模型概述

Stewart平台是一种六自由度并联机器人，由一个固定平台和一个移动平台组成，通过六个线性执行器（或称为作动器）连接。Simulink模型通常包括以下几个部分：

运动学逆解：计算给定平台位置和姿态时所需的作动器长度。
动力学分析：模拟平台的动力学行为。
控制器设计：实现对平台的精确控制。
三维可视化：显示平台的实时运动状态。

2. MATLAB/Simulink 模型构建

2.1 运动学逆解

function actuator_lengths = inverseKinematics(platform_position, platform_orientation)
    % 定义固定平台和移动平台上的点
    fixed_points = [0 0 0; 1 0 0; 0 1 0; -1 0 0; 0 -1 0]; % 固定平台上的点（简化）
    moving_points = [0 0 1; 1 0 1; 0 1 1; -1 0 1; 0 -1 1]; % 移动平台上的点（简化）

    % 应用平台位置和平移
    R = eul2rotm(platform_orientation); % 旋转矩阵
    T = trvec2tform(platform_position); % 平移向量转换为变换矩阵

    % 计算每个作动器的长度
    actuator_lengths = zeros(size(fixed_points, 1), 1);
    for i = 1:size(fixed_points, 1)
        % 将移动平台上的点转换到全局坐标系
        global_moving_point = T * (R * moving_points(i, :)');
        % 计算作动器长度
        actuator_lengths(i) = norm(global_moving_point - fixed_points(i, :)');
    end
end

2.2 动力学分析

使用Simscape Multibody进行动力学分析：

打开Simulink，创建一个新的Simscape Multibody项目。
导入或创建Stewart平台的3D模型。如果已有STL文件，可以直接导入；否则，可以在SolidWorks等软件中设计后导入。
添加关节和作动器。为每个作动器添加Prismatic Joint（平移关节），并设置相应的控制信号。
定义输入输出接口。包括平台位置和姿态的输入，以及各作动器长度的输出。

2.3 控制器设计

PID控制器用于控制每个作动器的伸缩：

function controlSignal = pidController(error, Kp, Ki, Kd)
    % PID控制器参数
    Kp = 1.0;
    Ki = 0.1;
    Kd = 0.05;

    % 更新误差积分和微分
    error_integral = error_integral + error;
    error_derivative = error - prev_error;

    % 计算控制信号
    controlSignal = Kp * error + Ki * error_integral + Kd * error_derivative;

    % 更新前一时刻误差
    prev_error = error;
end

2.4 三维可视化

使用MATLAB的plot3函数进行三维可视化：

% 示例数据
fixed_points = rand(6, 3); % 固定点位置
moving_points = rand(6, 3); % 移动点位置

% 绘制Stewart平台
figure;
hold on;
for i = 1:6
    plot3([fixed_points(i, 1), moving_points(i, 1)], ...
          [fixed_points(i, 2), moving_points(i, 2)], ...
          [fixed_points(i, 3), moving_points(i, 3)], 'r-', 'LineWidth', 2);
end
axis equal;
grid on;
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Stewart Platform Visualization');

3. Simulink 模型示例

以下是Simulink模型的基本结构：

输入模块：接收平台的位置和姿态。
逆解模块：计算作动器长度。
动力学模块：模拟平台的动力学行为。
控制器模块：实现PID控制。
输出模块：显示平台的实时运动状态。

4. 总结

通过上述步骤，你可以构建一个完整的Stewart平台仿真模型。希望这些信息对你有所帮助！
在这里插入图片描述
这张图片展示了一个在MATLAB Simulink中构建的Stewart平台仿真模型。为了更好地理解和使用这个模型，我将提供一个详细的解释，并附上相关的代码和说明。