Threes.js入门篇之4 - World View Projection

 在三维世界，一个模型要想最终呈现到一个照片上，需要经过三次矩阵变换，这三个矩阵分别是：

       模型矩阵（World） - 视图矩阵（View）- 投影矩阵（Projection）

一. 模型矩阵

       将 局部坐标系 下的模型坐标（相对于自身原点的坐标） 转化到 世界坐标系 下，通常称为World Matrix。

       可以理解为把多个不同坐标系下的子模型统一到一个世界坐标空间。

       局部坐标系（模型坐标）       -->    世界坐标系

             World_Matrix *  [x,y,z]   -->    [x',y',z']

                               M *  P[5,0,5]   -->    P[20,8,4]   对应下图中P点在世界坐标系下的坐标值。

              

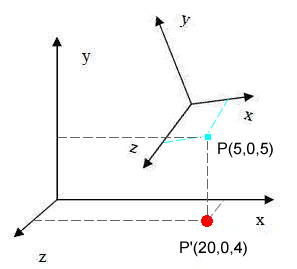
二. 视图矩阵

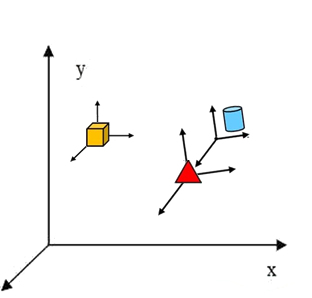
       将模型统一到一个坐标度量之后，需要将坐标变换到 观察者的视野范围内，也就是观测视角。

       世界坐标系      -->    视图坐标系（观察者） 

             View_Matrix *  [x',y',z']   -->    [x'',y'',z'']

        

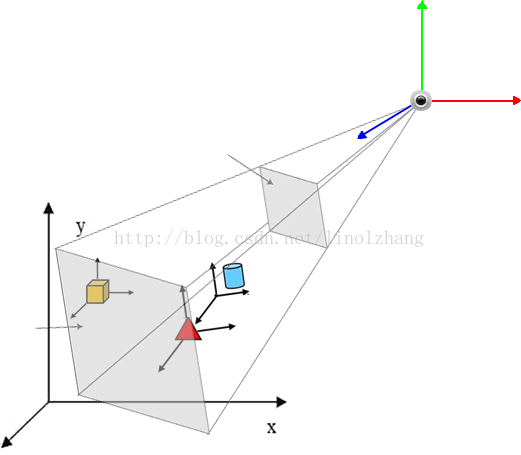
        通过 视图矩阵 将场景中所有模型的 世界坐标 转化到 视图坐标系（如上图 RGB坐标轴）。

三. 投影矩阵

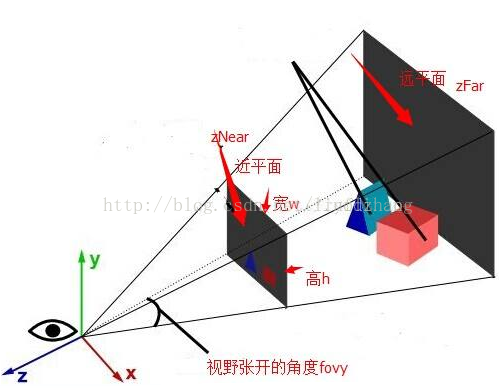
       将 用户视图（Viewer） 下的坐标，经过透视投影进行成像，将三维空间变换到图像空间。

       可以理解为 透视投影的成像，即从三维空间变换到图像空间。

       视图坐标系      -->    图像坐标系（UV空间） 

            Projection_Matrix *  [x'',y'',z'']   -->    [U,V,1]

        

       注：该图像来自于网上（不确定版权，如有侵权，还请告知！）

       因此，整个成像的过程可以用公式描述为：

                 [u,v,1] = Matrix_Projection * Matrix_View * Matrix_World * [x,y,z]