【机器学习】阿里云天池竞赛——工业蒸汽量预测（2）

机器学习经典赛题：工业蒸汽量预测（2）

3.1 特征工程的重要性和处理

特征是原始数据的数值表示。有多种方法可以将原始数据转换为数值型的表示，所以特征可以有多种形式。当然，特征必须采用可用的数据类型。事实上，特征还和模型相关联，这一点可能并不那么显而易见。有些模型更适合使用某种类型的特征，反之亦然。正确的特征应该适合当前的任务，并易于被模型所使用。特征工程就是在给定数据、模型和任务的情况下设计出最合适的特征的过程。

特征工程就是从原始数据提取特征的过程，这些特征可以很好地描述数据，并且利用特征建立的模型在未知数据上的性能表现可以达到最优（或者接近最佳性能）。特征工程一般包括特征使用、特征获取、特征处理、特征选择和特征监控。

业界广泛流传着这样一句话：“数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已”，具体来说，特征越好、灵活性越强，构建的模型越简单、性能越出色。如下图所示：

特征工程的处理流程为首先去掉无用特征，接着去除冗余的特征，如共线特征，并利用存在的特征、转换特征、内容中的特征以及其他数据源生成新特征，然后对特征进行转换（数值化、类别转换、归一化等），最后对特征进行处理（异常值、最大值、最小值，缺失值等）以符合模型的使用。

简单来说，特征工程的处理一般包括数据预处理、特征处理、特征选择等工作，而特征选择视情况而定，如果特征数量较多，则可以进行特征选择等工作。

3.2 数据预处理和特征处理

3.2.1 数据预处理

在进行特征提取之前，要对数据进行预处理，具体包括数据采集、数据清洗、数据采样。

1. 数据采集
   在数据采集之前需要明确几个问题：哪些数据对最后的预测结果有帮助，是否能采集到这一类数据，在线上实时计算时数据获取是否快捷。

2. 数据清洗
   大多时候机器学习算法就是一个加工机器，至于最后的产品如何，很大程度上取决于原材料的好坏。数据清洗就是去除“脏”数据，比如某些商品的刷单数据。如何判定数据为“脏”数据呢？

• 简答属性判定：身高为3米的人，一个月购买10万元的美发卡。
• 组合或统计属性判定：如号称在美国却一直是国内的新闻阅读用户。
• 补齐可对应的缺省值：将不可信的样本丢掉，不用缺省值极多的字段。

3. 数据采样
   数据在采集、清洗过以后，正负样本是不均衡的，所以要进行数据采样。采样的方法有随机采样和分层采样。但由于随机采样存在隐患，可能某次随机采样得到的数据很不均衡，因此更多的是根据特征进行分层抽样。
   正负样本不平衡的处理方法：

• 正样本>负样本，且量都特别大的情况：采用下采样（downsampling）的方法；
• 正样本>负样本，且量都不大的情况，可采用以下方法采集更多的数据：
  • 上采样（oversampling），比如图像识别中的镜像和旋转；
  • 修改**损失函数（loss function）**设置样本权重。

3.2.2 特征处理

特征处理的方法包括标准化、区间缩放法、归一化、定量特征二值化、定性特征哑编码、缺失值处理和数据转换。

1. 标准化
   标准化是依照特征矩阵的列处理数据，即通过求标准分数的方法，将特征转换为标准正态分布，并和整体样本分布相关。每个样本点都能对标准化产生影响。
   标准化需要计算特征的均值和标准差，公式如下：
   $$x^{\prime }=\frac{x-\bar{X}}{S}$$

from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris

iris = load_iris()
# 标准化，返回值为标准化后的数据
StandardScaler().fit_transform(iris.data)

运行结果：

2. 区间缩放法
   区间缩放法的思路有多种，常见的一种是利用两个最值（最大值和最小值）进行缩放。公式如下：
   $$x^{\prime }=\frac{x-Min}{Max-Min}$$
   代码如下：

from sklearn.preprocessing import MinMaxScaler

# 区间缩放，返回值为缩放到[0,1]区间的数据
MinMaxScaler().fit_transform(iris.data)

运行结果：

3. 归一化
   归一化是将样本的特征值转换到同一量纲下，把数据映射到[0,1]或者[a,b]区间内，由于其仅由变量的极值决定，因此区间缩放法是归一化的一种。
   注意：归一区间会改变数据的原始距离、分布和信息，但标准化一般不会。

规则为L2的归一化公式如下：
$$x^{\prime }=\frac{x}{\sqrt{{\sum }_j^{m}x[j{]}^2}}$$
代码如下：

from sklearn.preprocessing import Normalizer

# 归一化， 返回值为归一化后的数据
Normalizer().fit_transform(iris.data)

运行结果：

归一化与标准化的使用场景：

• 如果对输出结果范围有要求，则用归一化。
• 如果数据较为稳定，不存在极端的最大值或最小值，则用归一化。
• 如果数据存在异常值和较多噪声，则用标准化，这样可以通过中心化间接避免异常值和极端值的影响。
• 支持向量机（Support Vector Machine, SVM），K近邻（K-Nearest Neighbor, KNN）、主成分分析（Principal Component Analysis, PCA）等模型都必须进行归一化或标准化操作。

4. 定量特征二值化
   定量特征二值化的核心在于设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0。公式如下：
   $$x^{\prime }=\{\begin{array}{cc}1& x>threshold\\ 0& x\le threshold\end{array}$$

from sklearn.preprocessing import Binarizer

# 二值化，阈值设置为3， 返回值为二值化后的数据
Binarizer(threshold=3).fit_transform(iris.data)

5. 定性特征哑编码
   哑变量（Dummy Variable），也被称为虚拟变量，通常是人为虚设的变量，取值为0或1，用来反映某个变量的不同属性。将类别变量转换为哑变量的过程就是哑编码。而对于有 n个类别属性的特征，通常会以 1个类别特征为参照，再产生$n-1$个哑变量。

引入哑变量的目的是把原本不能定量处理的变量进行量化，从而评估定性因素对因变量的影响。

例如，假设特征“职业”的取值分别为工人、农民、学生、企业职员、其他等5种选项，那么我们可以将“工人”定义为（0,0,0,1）、“农民”定义为（0,0,1,0）、“学生”定义为（0,1,0,0）、“企业职员”定义为（1,0,0,0），“其他”是参考，为(0,0,0,0)。

通常会将原始的多分类变量转换为哑变量，在构建回归模型时，每一个哑变量都能得出一个估计的回归系数，这样使得回归的结果更易于解释，也更具有实际意义。

from sklearn.preprocessing import OneHotEncoder

# 对iris数据集的目标变量哑编码，返回值为哑编码后的数据
OneHotEncoder(categories='auto').fit_transform(iris.target.reshape((-1,1)))

运行结果：

<150x3 sparse matrix of type '<class 'numpy.float64'>'
	with 150 stored elements in Compressed Sparse Row format>

6. 缺失值处理
   当数据中存在缺失值时，用Pandas读取后特征均为NaN，表示数据缺失，即数据未知。例如，在iris数据集中加入几个空值（NaN）,然后使用impute库的SimpleImputer类对这个数据集进行缺失值计算。

对值缺失严重的可以采用dropna方法直接消除该特征或样本。而不想丢失数据信息，保留那些非缺失值数据的同时处理缺失值，要进行处理的数据集中包含缺失值一般步骤如下：

1. 使用字符串’nan’来代替数据集中的缺失值；
2. 将该数据集转换为浮点型便可以得到包含np.nan的数据集；
3. 使用sklearn.preprocessing.Imputer类来处理使用np.nan对缺失值进行编码过的数据集

from numpy import vstack,array,nan
from sklearn.impute import SimpleImputer

# 缺失值处理，返回值为缺失值后的数据
# 参数missing_value为缺失值的表示形式，默认为NaN
# 参数strategy为缺失值的填充方式，默认为mean（均值）
# vstack((array([nan,nan,nan,nan]),iris.data)) #将两个元素形状相同的数组进行垂直堆叠
SimpleImputer().fit_transform(vstack((array([nan,nan,nan,nan]),iris.data)))
# 上面等价于
# sim = SimpleImputer(missing_values=nan,strategy='mean')
# sim.fit_transform(vstack((array([nan,nan,nan,nan]),iris.data)))

运行结果

通过vstack将iris最上侧新加了一行nan，再用SimpleImputer对新的数据集进行缺失值处理，默认参数strategy为用mean填充。

7. 数据转换
   常见的数据转换有基于多项式、指数函数、对数函数的转换方式。
   （1）多项式转换——4个特征，度为2的多项式转换公式为
   $$\begin{gathered} (x_1^{\prime },x_2^{\prime },x_3^{\prime },x_4^{\prime },x_5^{\prime },x_6^{\prime },x_7^{\prime },x_8^{\prime },x_9^{\prime },x_{10}^{\prime },x_{11}^{\prime },x_{12}^{\prime },x_{13}^{\prime },x_{14}^{\prime },x_{15}^{\prime })= \\ (1,x_1,x_2,x_3,x_4,x_1^2,x_1\ast x_2,x_1\ast x_3,x_1\ast x_4,x_2^2,x_2\ast x_3,x_2\ast x_4,x_3^2,x_3\ast x_4,x_4^2) \end{gathered}$$
   例如，使用preprocessing库的PolynomialFeatures类对iris数据集进行多项式转换:

from sklearn.preprocessing import PolynomialFeatures

# 多项式转换
# 参考degree为度，默认值为2
PolynomialFeatures().fit_transform(iris.data) #(150, 15)

运行结果：

（2）对数变换
基于单变元函数的数据转换可以使用一个统一的方法完成。

例如，使用preprocessing库的FunctionTransformer类对iris数据集进行对数转换。这里的FunctionTransformer类主要是对数据进行转换，转化函数由自己定义，这里用log1p：返回一个数字加1后的自然对数 (底为 E), 即$log(x+1)$.

from numpy import log1p
from sklearn.preprocessing import FunctionTransformer

# 自定义转换函数为对数函数的数据转换
# 第一个参数是单变元函数
FunctionTransformer(log1p,validate=False).fit_transform(iris.data)

运行结果：

8. 特征处理小结
   下表对于特征处理中使用的sklearn类进行了归纳总结：

类	功能	功能
StandardScaler	无量纲化	标准化，基于特征矩阵的列，将特征值转换为服从标准正态分布
MinMaxScaler	无量纲化	区间缩放，基于最大值或最小值，将特征值转换到[0,1]区间内
Normalizer	归一化	基于特征矩阵的行，将样本向量转换为单位向量
Binarizer	定量特征二值化	基于给定阈值，将定量特征按阈值划分
OneHotEncoder	定性特征哑编码	将定性特征编码为定量特征
Imputer	缺失值处理	计算缺失值，缺失值有多种填充策略（均值等）
PolynomialFeatures	多项式数据转换	多项式数据转换
FunctionTransformer	自定义单元数据转换	使用单变量函数转换数据

3.3 特征降维

降维指的是采用某种映射方法，将高维向量空间的数据点映射到低维的空间中。降维的本质是学习一个映射函数$f:x->y$，其中$x$是原始数据点的表达，多采用向量表达；$y$是数据点映射后的低维向量表达，通常$y$的维度小于$x$的维度（当然提高维度也是可以的）。$f$函数的定义比较灵活，可以是显示或隐式的，也可以是线性或非线性的。

在原始的高维空间中，向量数据包含冗余信息及噪声信息，其在实际应用中会对模型识别造成误差，降低准确率；而通过特征降维可以减少冗余信息造成的误差，从而提高识别的精度。特征降维的常用方法有特征选择和线性降维。

3.3.1 特征选择

1. 特征选择的定义
   特征选择是在数据分析和简单建模中最常用的特征降维手段。其比较简单粗暴，即映射函数直接将不重要的特征删除，不过这样会造成特征信息的丢失，不利于模型精度。由于数据分析以抓住主要影响因子为主，变量越少越有利于分析，因此特征选择常用于统计分析模型中；在超高维数据分析（特征维度过高可以直接批量删除）或者建模预处理中也会经常使用，如基因序列建模。特征选择的目标如下表所示：

特征选择的目标	说明
特征是否发散	如果一个特征不发散，即方差接近0，就说明样本在这个特征上基本没有差异，这个特征对于样本的区分没有作用
特征与目标变量的相关性	与目标相关性高的特征应当优先选择

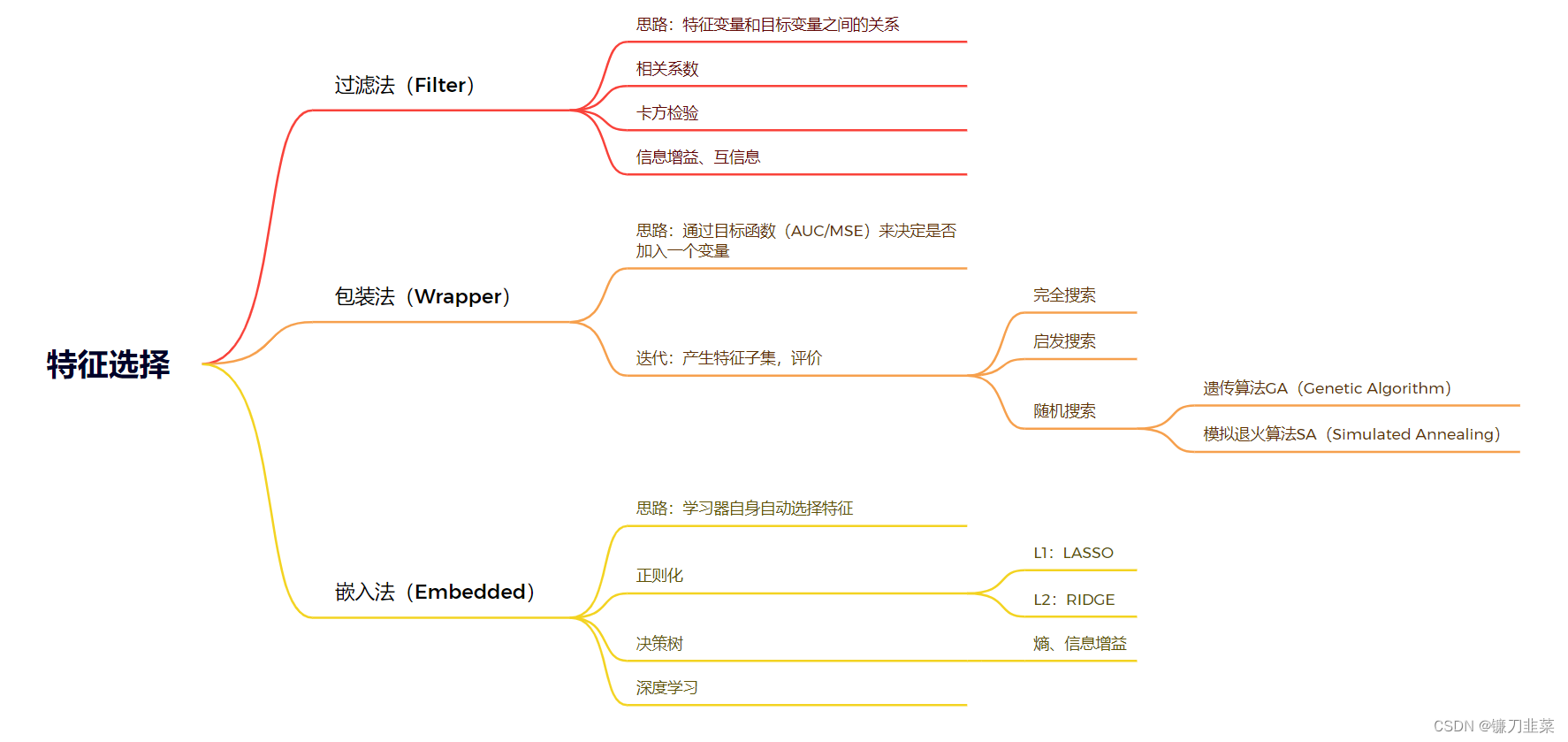
2. 特征选择的方法
   特征选择的方法有过滤法（Filter）、包装法（Wrapper）和嵌入法（Embedded）。

• 过滤法：按照发散性或者相关性对各个特征进行评分，通过设定阈值或者待选择阈值的个数来选择特征。
• 包装法：根据目标函数（通常是预测效果评分）每次选择若干特征，或者排除若干特征
• 嵌入法：使用机器学习的某些算法和模型进行训练，得到各个特征的权值系数，并根据系数从小到大选择特征。这一方法类似于过滤法，区别在于它通过训练来确定特征的优劣。
  这三类方法的特点如下图所示：
  

3. 特征选择在中的具体实现
   下表列出了sklearn中具体的特征处理的类和所属方法：

类	所属方法	具体方法
VarianceThreshold	Filter	方差选择法
SelectKBest	Filter	将可选相关系数、卡方检验或最大信息系数作为得分计算的方法
RFE	Wrapper	递归消除特征法
SelectFromModel	Embedded	基于模型的特征选择法

1) VarianceThreshold
使用方差选择法，先要计算各个特征的方差，然后根据阈值选择方差大于阈值的特征。

from sklearn.feature_selection import VarianceThreshold
from sklearn.datasets import load_iris

iris = load_iris()

# 方差选择法，返回值为特征选择后的数据
# 参数threshold为方差的阈值
VarianceThreshold(threshold=0.6).fit_transform(iris.data)  #(150,1) 筛选出特征方差大于0.6的列的数据

运行结果：

2) SelectKBest
（1）相关系数法。使用相关系数法，先要计算各个特征对目标值的相关系数及相关系数的P值，然后根据阈值筛选特征。

import numpy as np
from sklearn.datasets import load_iris

iris = load_iris()
from sklearn.feature_selection import SelectKBest
from scipy.stats import pearsonr

# 选择K个最好的特征，返回选择特征后的数据
# 第一个参数为计算评估特征的函数，该函数输入特征矩阵和目标向量，输出二元组（评分，P值）的数组，数组第i项为第i个特征的评分和P值。
# 在此定义为计算相关系数。
# 第二个参数k为选择的特征个数
SelectKBest(lambda X, Y: np.array(list(map(lambda x: pearsonr(x, Y), X.T))).T[0], k=2).fit_transform(iris.data, iris.target)  #最后两个特征相关系数是最强的

结果显示最后两列的特征系数最高，可以通过DataFrame.corr()来计算相关系数:

（2）卡方检验。
经典的卡方检验是检验定性自变量与定性因变量的相关性。假设自变量有N种取值，因变量有M种取值，考虑自变量等于$i$且因变量等于$j$的样本频数的观察值与期望值的差距，构建统计量：
$$x^2=\sum \frac{(A-E{)}^2}{E}$$
用feature_selection库的SelectKBest类结合卡方检验来选择特征。

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

# 选择k个最好的特征，返回选择特征后的数据
SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)

（3）最大信息系数法(Maximal information coefficient, MIC)。MIC是基于互信息理论的，经典的互信息也是评价定性自变量与定性因变量相关性的方法。互信息计算公式如下：
$$I(X;Y)=\sum _{x\in y}\sum _{y\in x}p(x,y)\log \frac{p(x,y)}{p(x)p(y)}$$

from sklearn.feature_selection import SelectKBest
from minepy import MINE


# 由于MINE的设计不是函数式的，因此需要定义mic方法将其转换为函数式，返回一个二元组，二元组的第二项设置成固定的P值，为0.5
def mic(x, y):
    m = MINE()
    m.compute_score(x, y)
    return (m.mic(), 0.5)


#  选择K个最好的特征，返回特征选择后的数据
SelectKBest(
    lambda X, Y: np.array(list(map(lambda x: mic(x, Y), X.T))).T[0], k=2
).fit_transform(iris.data, iris.target)

不过在使用上，minepy非常不好安装，正常安装会提出需要安装c++的编译包，也可以选择使用第三方的minepy工具包.

3) RFE（Recursive feature elimination）
递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。用feature_selection库的RFE类来选择特征。

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

# 递归特征消除法，返回特征选择后的数据
# 参数estimator为基模型
# 参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(multi_class='auto',
                                 solver='lbfgs',
                                 max_iter=500),
    n_features_to_select=2).fit_transform(iris.data, iris.target)

4）SelectFromModel
SelectFromModel主要采用基于模型的特征选择法，常见的有基于惩罚项的特征选择法和基于树模型的特征选择法。
（1）基于惩罚项的特征选择法使用带惩罚项的基模型，除了能筛选出特征，也进行了降维。
使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型来选择特征。

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression

# 将带L1惩罚项的逻辑回归作为基模型的特征选择
SelectFromModel(estimator=LogisticRegression(penalty='l2',
                                             C=0.1,
                                             solver='lbfgs',
                                             multi_class='auto')).fit_transform(iris.data, iris.target)

（2）基于树模型的特征选择法。在树模型中，GBDT（Gradient Boosting Decision Tree，梯度提升迭代决策树）也可用来作为基模型进行特征选择。

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier

# 将GBDT作为基模型的特征选择
SelectFromModel(estimator=GradientBoostingClassifier()).fit_transform(iris.data,iris.target)

3.3.2 线性降维

线性降维常用的方法有主成分分析法（PCA）和线性判别分析法（LDA）。

1. 主成分分析法（无监督）
   主成分分析法是最常用的线性降维方法，主要原理是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此达到使用较少的数据维度来保留较多的原数据点特性的效果。

from sklearn.decomposition import PCA

# 主成分分析法，返回降维后的数据
# 参数n_components为主成分的数目
PCA(n_components=2).fit_transform(iris.data)

注意，这里返回的结果是原始的四个特征综合后的两个特征。而且从代码中可以看出PCA并不需要target目标变量，所以其属于无监督算法的一种。

2. 线性判别分析法（有监督）
   线性判别分析法（Linear Discriminant Analysis，LDA），也叫作Fisher线性判别（Fisher Linear Discriminant，FLD），是一种有监督的线性降维算法。与PCA尽可能多地保留数据信息不同，LDA的目标是使降维后的数据点尽可能容易被区分，其利用了标签的信息。

假设原始线性数据为$X$，我们希望找到映射向量$a$，使得$aX$后的数据点能够保持一下两种性质：①同类的数据点尽可能接近；②不同类的数据点尽可能分开。

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

# 线性判别分析法，返回降维后的数据
# 参数n_compoents为降维后的特征数
LDA(n_components=2).fit_transform(iris.data, iris.target)

3.4 特征工程实战

导入蒸汽数据：

train_data_file='../data/zhengqi_train.txt'
test_data_file='../data/zhengqi_test.txt'

train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')

3.4.1 异常值分析

绘制各个特征的箱线图：

# 绘制各个特征的箱线图
plt.figure(figsize=(18, 10))
plt.boxplot(x=train_data.values, labels=train_data.columns)
plt.hlines([-7.5, 7.5], 0, 40, colors='r')
plt.show()

运行结果：

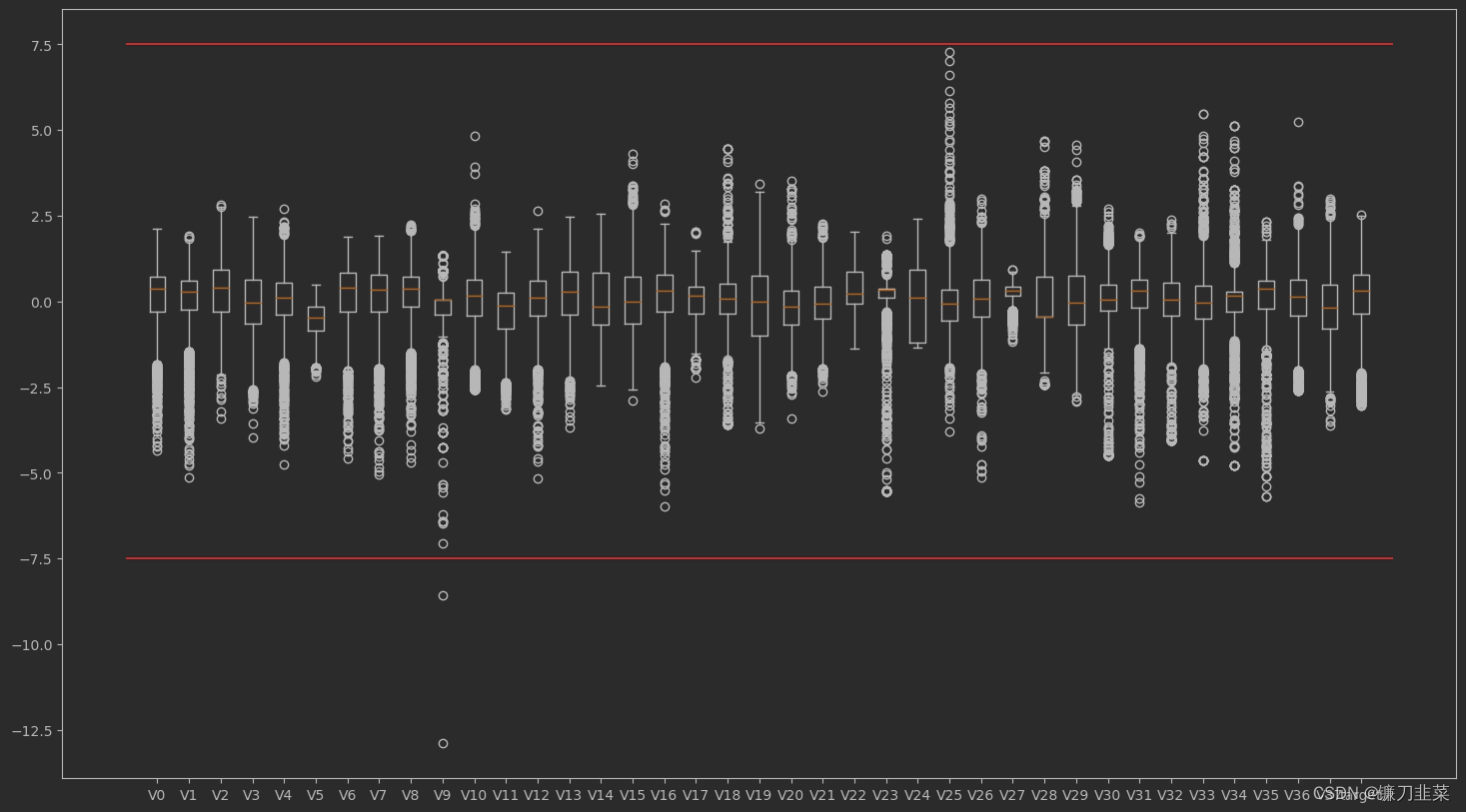
从箱线图可以看出，有些特征存在明显的异常值，如V9变量。下面分别对训练集和测试集中的异常值删除：

from IPython.core.display_functions import display

train_data = train_data[train_data['V9'] > -7.5]
test_data = test_data[test_data['V9'] > -7.5]
display(train_data[train_data['V9'] > -7.5].describe())
display(test_data[test_data['V9'] > -7.5].describe())

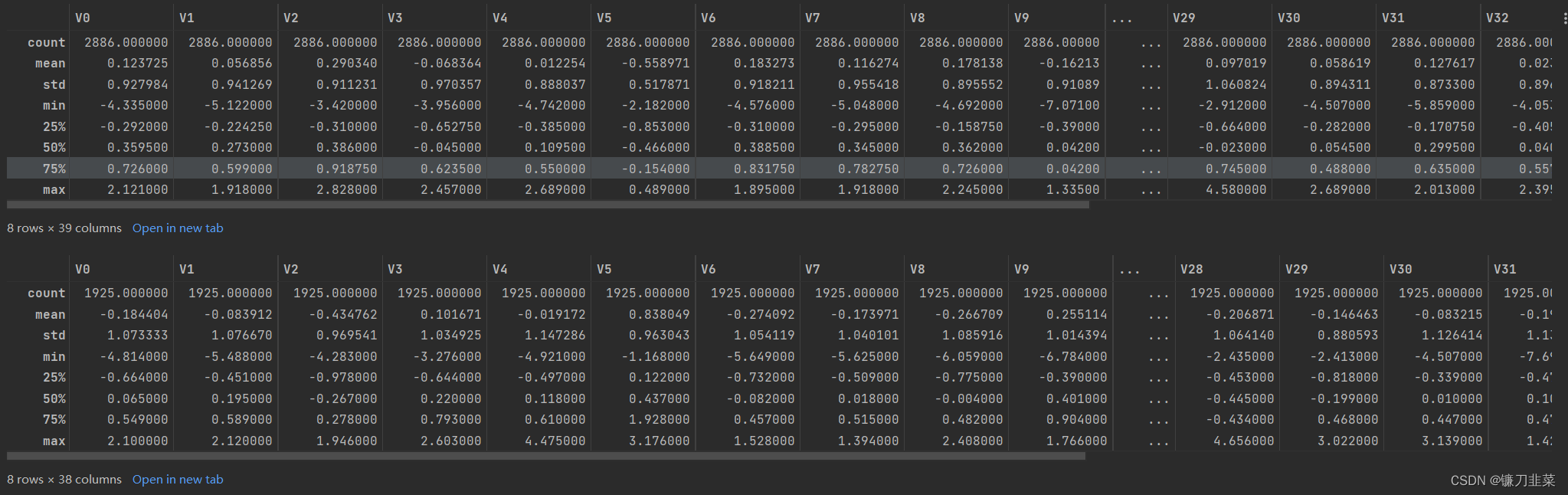
3.4.2 最大值和最小值的归一化

对数据进行归一化处理：

from sklearn import preprocessing

features_columns = [col for col in train_data.columns if col not in ['target']]
min_max_scaler = preprocessing.MinMaxScaler()
min_max_scaler = min_max_scaler.fit(train_data[features_columns])

train_data_scaler = min_max_scaler.transform(train_data[features_columns])
test_data_scaler = min_max_scaler.transform(test_data[features_columns])

train_data_scaler = pd.DataFrame(train_data_scaler)
train_data_scaler.columns = features_columns

test_data_scaler = pd.DataFrame(test_data_scaler)
test_data_scaler.columns = features_columns
train_data_scaler['target'] = train_data['target']
display(train_data_scaler.describe())
display(test_data_scaler.describe())

运行结果：

3.4.3 查看数据分布

在前面的数据探索中，通过KDE分布对比了特征变量在两个数据集中的分布情况，这里不再重复过程。对比后发现：特征变量V5，V9，V11，V17，V22，V28在训练集和测试集中的分布差异较大，会影响模型的泛化能力，故删除这些特征。

drop_col = 6
drop_row = 1
plt.figure(figsize=(5 * drop_col, 5 * drop_row))

for i, col in enumerate(["V5", "V9", "V11", "V17", "V22", "V28"]):
    ax = plt.subplot(drop_row, drop_col, i + 1)
    ax = sns.kdeplot(train_data[col], color="Red", shade=True)
    ax = sns.kdeplot(test_data[col], color="Blue", shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train", "test"])
plt.show()

特征变量V5，V9，V11，V17，V22，V28在训练集和测试集中的分布比对：

3.4.4 特征相关性

计算特征相关性，以热力图形式可视化显示：

plt.figure(figsize=(20, 16))
column = train_data_scaler.columns.tolist()  #获取训练集的特征列表
mcorr = train_data_scaler[column].corr(method="spearman")
mask = np.zeros_like(mcorr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
cmap = sns.diverging_palette(220, 10, as_cmap=True)
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')
plt.show()

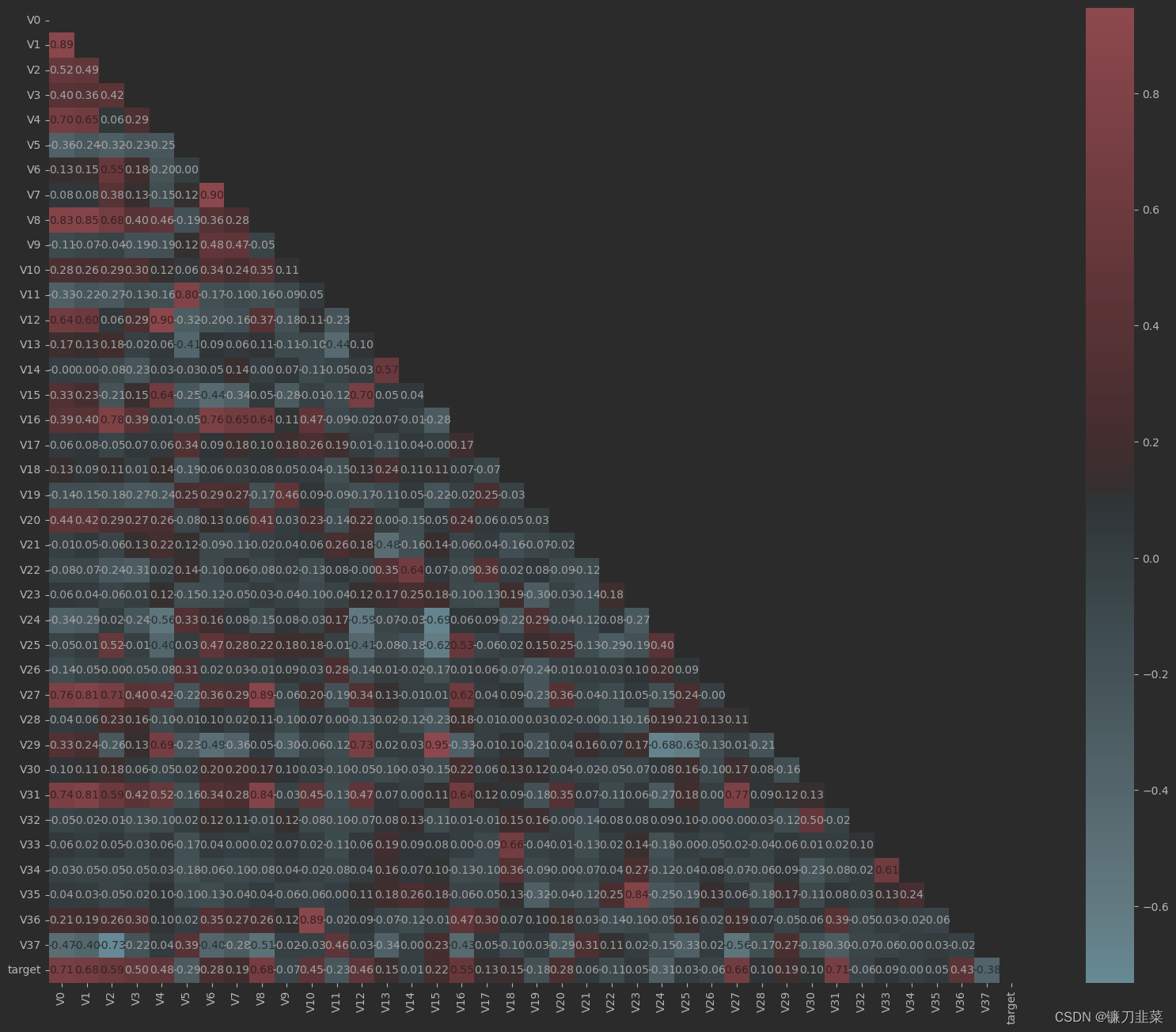
3.4.5 特征降维

首先是特征相关性的初筛，计算相关性系数并筛选大于0.1的特征变量。

还可以对相关性系数进行排序显示：

3.4.6 多重共线性分析

多重共线性分析的原则是特征组之间的相关系系数较大，即特征变量之间的相关系系数较大，故可能存在较大的共线性影响，这会导致模型估计不准确。因此，后续要使用PCA对数据进行处理，去除多重共线性。
对数据进行多重共线性计算，代码如下：

from statsmodels.stats.outliers_influence import variance_inflation_factor

# 多重共线性方差膨胀因子
# 多重共线性
# new_numerical的特征变量可以自行根据相关性矩阵看出并过滤筛选
new_numerical = ['V0', 'V2', 'V3', 'V4', 'V5', 'V6', 'V10', 'V11', 'V13', 'V15', 'V16', 'V18', 'V19', 'V20', 'V22',
                 'V24', 'V30', 'V31', 'V37']
X = np.matrix(train_data_scaler[new_numerical])
VIF_list = [variance_inflation_factor(X, i) for i in range(X.shape[1])]
VIF_list

注意：new_numerical的特征变量可以自行根据相关性矩阵看出并过滤筛选。

3.4.7 PCA处理

利用PCA方法去除数据的多重共线性，并进行降维。PCA处理后可保持90%的信息数据：

from sklearn.decomposition import PCA

# 保持90%的信息
pca = PCA(n_components=0.9)
new_train_pca_90 = pca.fit_transform(train_data_scaler.iloc[:, 0:-1])
new_test_pca_90 = pca.transform(test_data_scaler)
new_train_pca_90 = pd.DataFrame(new_train_pca_90)
new_test_pca_90 = pd.DataFrame(new_test_pca_90)
new_train_pca_90['target'] = train_data_scaler['target']
new_train_pca_90.describe()

查看原始数据信息并于PCA处理后的数据进行比对：

PCA处理后保留16个主成分，代码如下：

pca = PCA(n_components=16)
new_train_pca_16 = pca.fit_transform(train_data_scaler.iloc[:, 0:-1])
new_test_pca_16 = pca.transform(test_data_scaler)
new_train_pca_16 = pd.DataFrame(new_train_pca_16)
new_test_pca_16 = pd.DataFrame(new_test_pca_16)
new_train_pca_16['target'] = train_data_scaler['target']
new_train_pca_16.describe()

运行结果：

参考资料

[1] 《阿里云天池大赛赛题解析——机器学习篇》
[2] scikit-learn 中 OneHotEncoder 解析
[3] sklearn 的 PolynomialFeatures 的用法
[4] 为什么要使用多项式回归
[5] 最大信息系数（MIC）
[6] Python的第三方库minepy安装解决方案