【图神经网络】使用DGL入门异构图神经网络

什么是异构图？

传统同构图（Homogeneous Graph）数据中只存在一种节点和边，因此在构建图神经网络时所有节点共享同样的模型参数并且拥有同样维度的特征空间。而异构图（Heterogeneous Graph）中可以存在不只一种节点和边，因此允许不同类型的节点拥有不同维度的特征或属性。

这一特点使得异构图的应用十分广泛。事实上，如果用图来描述我们和周围事物的关系就会发现所产生的图都是天然异构的。比如今天看了电影《流浪地球》，那“我”作为观众和电影《流浪地球》之间就建立了“看了”这一关系。异构图可以用来描述这种交互关系的集合。这个图分“观众”和“电影”两类节点，以及“看了”这一类边。“我”作为观众，和电影所具有的属性一定是不同的，需要用不同的模型或者不同的特征维度来表达。这张图就天然具有了异构性。

再比如我去豆瓣上给《流浪地球》评了8分，那“我”和《流浪地球》之间就又建立了“评分”这一关系。“评分”和“看了”的属性也一定是不同的，如前者包含评分分数，后者则包含票价等。

因此，很多用于机器学习的数据都可以用异构图来建模，而需要解决的任务也可以通过学习图上的点和边，或是整张图的表示来解决。这里举几个例子。

异构图的常见建模场景

推荐系统

图1：使用异构图建模推荐系统

常见的推荐系统数据由用户和商品的交互信息组成。这些交互信息可以用图来表示（图1）。由于用户节点可能包含用户的年龄、职业等个人信息，而商品节点则包含内容、价格等商品特有的信息，所以该图是一个异构图。

推荐系统可能感兴趣的内容包括：

• 判断某个客户是否会观看某部电影，以及在什么样的促销下会购票。这个问题可以转化成链接预测（Link Prediction）问题：判断两个点之间是否会有连边。
• 判断某个客户是否存在恶意刷分，或者某部电影是否遭到恶意刷分。根据标注是否存在，这个问题可以转化成半监督节点分类（Semi-supervised Node Classification）或者无监督的异常检测（Anomaly Detection）问题。

学术网络

学术网络的图结构更复杂一些。它可以包含“论文”、“作者”、“会议”和“机构”等节点类型。每个作者会隶属于某些机构，发表某些论文，而每篇论文又会被发表在某个会议上，也会引用其它的论文。每个节点同样可以有自己的特征——如论文可以用摘要当作特征等。同样，这些关系可以表示成一张异构图（图2）。

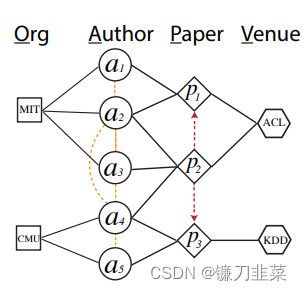
图2：学术网络

同样，链接预测和节点分类问题也适用于学术网络中。例如预测某个作者的研究领域或所属的研究团队、一篇论文或者一个作者的影响力等等。

知识图谱

知识图谱由于包含不同种类的节点和边，是一张天然的异构图。如下图，“人物”、“职业”和“荣誉”等都可以作为节点类型，而节点之间的关系也有“就职”、“获得荣誉”等多种类别。

图3：Wikidata知识图谱示例

图嵌入学习在知识图谱上也是一个很重要的任务。它的目标是对每一个节点和每一类关系学习一个高维向量表示。此外，知识图谱补全、基于知识图谱的推理以及将知识图谱与其他系统结合（比如推荐系统）等也是重要的任务。

针对异构图的图神经网络有哪些？

针对异构图设计图神经网络还是个非常新的方向。虽然论文不多，但已经在一些场景中取得了很不错的效果。这里简单介绍两个模型。

Relational Graph Convolutional Network (RGCN)

文章链接：https://arxiv.org/abs/1703.06103

Schlichtkrull, M., Kipf, T.N., Bloem, P., van den Berg, R., Titov, I., Welling, M. (2018). Modeling Relational Data with Graph Convolutional Networks. In: , et al. The Semantic Web. ESWC 2018. Lecture Notes in Computer Science(), vol 10843. Springer, Cham. https://doi.org/10.1007/978-3-319-93417-4_38

RGCN是一个在异构图上学习节点表示的早期工作（2017年）。与Graph Convolutional Network（GCN）类似，它仍然基于消息传递（Message Passing）。但与GCN不同，每条边上的消息通过每类边独有的线性变换得到。
$$h_i^{(l+1)}=\sigma (\sum _{r=1}^R\sum _{j\in {\mathcal{N}}_{i,r}}\frac{1}{c_{i,r}}{W}_r^{(l)}{h}_j^{(l)}+W_0^{(l)}{h}_i^{(l)})$$
RGCN可以用于节点分类和链接预测等任务。

Graph Convolutional Matrix Completion (GCMC)

文章链接：https://arxiv.org/abs/1706.02263
GCMC是在异构图上做产品推荐任务的一个尝试。它在一个由观众和电影组成的二分图上训练。观众和电影有各自的特征，而且每一条边上有对应的观众对电影的评分。GCMC将每一种评分视为一类边。

图构建完成后，每个节点通过消息传递的形式，汇总从自己邻居传递来的消息，去更新自己的表示。与RGCN不同的是，GCMC只进行一层消息传递：
$$h_i=\sigma [accum(\sum _{j\in N_{i,1}}{\mu }_{j\to i,1},...,\sum _{j\in N_{i,R}}{\mu }_{j\to i,R})]$$
消息同样是由源节点的原表示通过线性变换得到。与RGCN类似，每类边都有自己线性变换的参数矩阵。不同之处在于多关系累和函数accum有各种灵活选择。
$${\mu }_{j\to i,r}=\frac{1}{c_{ij}}{W}_r{x}_j$$
GCMC算出两类点的最终表示之后，再通过softmax得出某个交互下每种评分的概率：
$$u_i=\sigma (W{h}_i)$$
$$v_j=\sigma (W{h}_j)$$
$$p(M_{ij}=r)=\frac{exp(u_i^T{Q}_r{v}_j)}{{\sum }_{s\in R}exp(u_i^T{Q}_s{v}_j)}$$
除了以上模型外，还有诸如Heterogeneous Graph Attention Network (HAN)，Knowledge Graph Convolution Networks for Recommender Systems (KGCN) 等关于异构图的好工作。此外，在网络嵌入（network embedding）方向还有如metapath2vec等经典的工作。

• Heterogeneous Graph Attention Network (WWW’19)
• Knowledge Graph Convolution Networks for Recommender Systems (WWW’19)
• HetGNN: Heterogeneous Graph Neural Network (KDD’19)
• Metapath-guided Heterogeneous Graph Neural Network for Intent Recommendation (KDD’19)
• KGAT: Knowledge Graph Attention Network for Recommendation (KDD’19)
• metapath2vec: Scalable Representation Learning for Heterogeneous Networks (KDD’17)

DGL中的异构图神经网络代码

DGl中支持异构图神经网络，以RGCN层为例，代码如下：

图四：DGL中基于异构图的RGCN层实现代码

此外，DGL也发布了训练知识图谱嵌入（Knowledge Graph Embedding）专用包DGL-KE，在许多经典的图嵌入模型上都获得了性能提升。

注意：上述内容中所涉及的代码和研究进展近年来发展迅速，已有不少新方法，需要读者自行更新。

参考资料

[1] RGCN ：GCN 在多边类型的应用
[2] GCMC - Graph Convolutional Matrix Completion 图卷积矩阵补全 KDD 2018
[3] DGL异构图教程：https://docs.dgl.ai/tutorials/hetero/1_basics.html