损失函数
在逻辑回归建立过程中,我们需要一个关于模型参数的可导函数,并且它能够以某种方式衡量模型的效果。这种函数称为损失函数(loss function)。
损失函数越小,则模型的预测效果越优。所以我们可以把训练模型问题转化为最小化损失函数的问题。
损失函数有多种,此次介绍分类问题最常用的交叉熵(cross entropy)损失,并从信息论和贝叶斯两种视角阐释交叉熵损失的内涵。
K-L散度与交叉熵
-
随机变量X有k种不同的取值: X 1 , X 2 , X 3 , … … , X k X^1, X^2, X^3 ,…… ,X^k X1,X2,X3,……,Xk。 记X的取值 X i X^i Xi 的概率为p(X= X i X^i Xi) ,简写为P( X i X^i Xi) .
-
克劳德**·** 香农定义了信息的信息量:
I ( X = X i ) = log 1 p ( X i ) = − log p ( X i ) I(X = X^i) = \log \frac{1}{p(X^i)} = - \log p(X^i) I(X=Xi)=logp(Xi)1=−logp(Xi)
注:其中对数可以以任意合理数为底,如 2、e。使用不同的底数所得到的信息量之间相差一个常系数。
若以2为底,信息量的单位是bit ,I(X= X i X^i Xi )是X = X i X^i Xi 这条信息的自信息量(self-information) .
-
自信息量I随着概率P( X i X^i Xi)的图像变化如下:
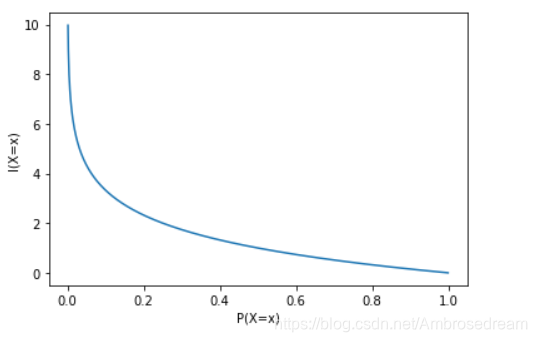
自信息量背后的含义:信息中事件发生的概率越小,则信息量越大。
举例:假如有人告诉你即将开奖的彩票中奖号码是777777777,这条信息的价值很高,类似事情发生概率极小。假如有人告诉你明天太阳会升起,这件事对你来说价值很低,但是他发生的概率却很高。所以我们会觉得彩票的开奖号信息量很大,太阳升起的信息量较小。
-
我们令信息源X 取不同的值 x 1 , x 2 , x 3 . . . x k x^1, x^2 , x^3 ... x^k x1,x2,x3...xk 的概率分布分别为 p ( x 1 ) p ( x 2 ) p ( x 3 ) . . . p ( x k ) p(x^1) p(x^2) p(x^3) ... p(x^k) p(x1)p(x2)p(x3)...p(xk) .
-
定义信息源 X的熵(entropy)为:
H§ = ∑ i = 1 K P ( x i ) log 1 P ( x i ) = − ∑ i = 1 K P ( x i ) log P ( x i ) \sum_{i=1}^K P(x^i) \log \frac{1}{P(x^i)} = - \sum_{i=1}^K P(x^i)\log P(x^i) ∑i=1KP(xi)logP(xi)1=−∑i=1KP(xi)logP(xi)
-
信息源由概率分布p描述,s所以熵是p的函数,熵的概念来自热力学。H§又称平均信息。
-
根据公式我们可以看出,H§是将X所有取值的自信息量以概率为权重取平均。
-
对于两个概率分布p和q, 定义p和q的K-L散度(kullback-leibler divergence)是:
K L D ( p ∣ ∣ q ) = ∑ i = 1 k p ( x i ) log p ( x i ) q ( x i ) = − ∑ i = 1 k p ( x i ) log q ( x i ) − H ( p ) KLD(p||q) = \sum_{i=1}^k p(x^i) \log \frac{p(x^i)}{q(x^i)} = - \sum_{i=1}^k p(x^i) \log q(x^i) - H(p) KLD(p∣∣q)=∑i=1kp(xi)logq(xi)p(xi)=−∑i=1kp(xi)logq(xi)−H(p)
-
K-L散度是 log p ( x i ) q ( x i ) \log \frac{p(x^i)}{q(x^i)} logq(xi)p(xi) 在分布p上的期望。(注:KLD(p||q) ≠ \neq = KLD(q||p))
-
根据上述公式我们可以发现,当 p ( x i ) 和 q ( x i ) p(x^i)和q(x^i) p(xi)和q(xi) 相等时, log p ( x i ) q ( x i ) = 0 \log \frac{p(x^i)}{q(x^i)} =0 logq(xi)p(xi)=0 所以KLD散度等于0。所以说两个同分布的KLD散度为0,所以我们一般使用KLD描述两个概率分布之间的相似度。
-
我们定义交叉熵:
H ( p , q ) = − ∑ i = 1 k p ( x i ) log q ( x i ) H(p,q) = - \sum_{i=1}^k p(x^i) \log q(x^i) H(p,q)=−∑i=1kp(xi)logq(xi)
-
所以根据上述两式,有:
H ( p , q ) = K L D ( p ∣ ∣ q ) + H ( p ) H(p,q) = KLD(p||q) + H(p) H(p,q)=KLD(p∣∣q)+H(p)
-
分布p和q的交叉熵等于它们的K-L散度加上p的熵。现在假设分布 p p p固定,则 H ( p , q ) H(p,q) H(p,q)与 K L D ( p ∣ ∣ q ) KLD(p||q) KLD(p∣∣q)之间只相差一个常数 H ( p ) H(p) H(p),所以此时 H ( p , q ) H(p,q) H(p,q)也可以被用来描述两个分部之间的相似程度。即: H ( p , q ) H(p,q) H(p,q)越小,p,q越相似。
-
对于一个训练样本{ x i , y i {x^i, y^i} xi,yi } 可以标签 y i y^i yi 给出了一个类别的概率分布:
-
P ( x i ∈ p ) = y i , P ( x i ∈ n ) = 1 − y i , i = 1 , … … , M P(x^i \in p) = y^i , P(x^i \in n) = 1-y^i , i= 1,……,M P(xi∈p)=yi,P(xi∈n)=1−yi,i=1,……,M
-
我们将逻辑回归模型的输出看做一个分布Q:
-
Q ( x i ∈ p ) = 1 1 + e − b − W T x i , Q ( x i ∈ n ) = 1 1 + e b + w T x i , i = 1 , … … , M Q(x^i \in p) = \frac{1}{1+e^{-b-W^Tx^i}} , Q(x^i \in n) = \frac{1}{1+e^{b+w^Tx^i}} , i=1,……,M Q(xi∈p)=1+e−b−WTxi1,Q(xi∈n)=1+eb+wTxi1,i=1,……,M
-
所以我们希望回归模型的准确率尽可能地高,即是希望分布Q与训练集P的分布尽可能地相似,由此我们可以使用交叉熵来描述输出分布于标签分布的相似度,也就是我们所说的损失函数(loss)
l o s s ( w , b ∣ x i , y i ) = − y i log 1 1 + e − b − W T x i − ( 1 − y i ) log 1 1 + e b + w T x i i = 1 , . . . , M loss(w,b|x^i,y^i) = -y^i\log \frac{1}{1+e^{-b-W^Tx^i}} - (1-y^i)\log\frac{1}{1+e^{b+w^Tx^i}} i= 1,...,M loss(w,b∣xi,yi)=−yilog1+e−b−WTxi1−(1−yi)log1+eb+wTxi1i=1,...,M
上式是模型在一个样本的交叉熵,其值越小,预测分布于标签给出分布越相似。
l o s s ( w , b ∣ x i , y i ) = 1 M ∑ i = 1 M ( − y i log 1 1 + e − b − W T x i − ( 1 − y i ) log 1 1 + e b + w T x i ) i = 1 , . . . , M loss(w,b|x^i,y^i) = \frac{1}{M} \sum_{i=1}^M( -y^i\log \frac{1}{1+e^{-b-W^Tx^i}} - (1-y^i)\log\frac{1}{1+e^{b+w^Tx^i}} )i= 1,...,M loss(w,b∣xi,yi)=M1∑i=1M(−yilog1+e−b−WTxi1−(1−yi)log1+eb+wTxi1)i=1,...,M
上式是样本的平均交叉熵,作为模型的损失函数。








 本文深入解析了交叉熵损失函数在逻辑回归模型中的应用,通过信息论和贝叶斯视角阐述了其数学原理,展示了如何利用交叉熵评估模型预测与真实标签的相似度。
本文深入解析了交叉熵损失函数在逻辑回归模型中的应用,通过信息论和贝叶斯视角阐述了其数学原理,展示了如何利用交叉熵评估模型预测与真实标签的相似度。

















 1428
1428

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










