Triangulation by Ear Clipping

Triangulation by Ear Clipping

---

David Eberly, Geometric Tools, Redmond WA 98052
https://www.geometrictools.com/
This work is licensed under the Creative Commons Attribution 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ or send a letter to Creative Commons,PO Box 1866, Mountain View, CA 94042, USA.
Created: November 18, 2002
Last Modi_ed: August 16, 2015

---

1 Introduction

A classic problem in computer graphics is to decompose a simple polygon into a collection of triangles whose vertices are only those of the simple polygon. By definition, a simple polygon is an ordered sequence of n points, V0 through Vn-1. Consecutive vertices are connected by an edge <Vi,Vi+1>, 0 ≤ i ≤ n - 2, and an edge <Vn-1,V0> connects the first and last points. Each vertex shares exactly two edges. The only place where edges are allowed to intersect are at the vertices. A typical simple polygon is shown in Figure 1.

---

Figure 1. The left polygon is simple. The middle polygon is not simple since vertex 1 is shared by more than two edges. The right polygon is not simple since the edge connecting vertices 1 and 4 is intersected by other edges at points that are not vertices.

            

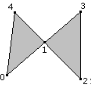
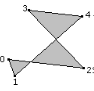
           Simple                   nonsimple          nonsimple

---

If a polygon is simple, as you traverse the edges the interior bounded region is always to one side. I assume that the polygon is counterclockwise ordered so that as you traverse the edges, the interior is to your left.The vertex indices in Figure 1 for the simple polygon correspond to a counterclockwise order.

The decomposition of a simple polygon into triangles is called a triangulation of the polygon. A fact from computational geometry is that any triangulation of a simple polygon of n vertices always has n-2 triangles.Various algorithms have been developed for triangulation, each characterized by its asymptotic order as n grows without bound. The simplest algorithm, called ear clipping, is the algorithm described in this document. The order is O(n2). Algorithms with better asymptotic order exist, but are more dificult to implement. Horizontal decomposition into trapezoids followed by identification of monotone polygons that are themselves triangulated is an O(n log n) algorithm [1, 3]. An improvement using an incremental randomized algorithm produces an O(n log* n) where log* n is the iterated logarithm function [5]. This function is effectively a constant for very large n that you would see in practice, so for all practical purposes the randomized method is linear time. An O(n) algorithm exists in theory [2], but is quite complicated. It appears that no implementation is publicly available.

 

2 Ear Clipping

An ear of a polygon is a triangle formed by three consecutive vertices Vi0 , Vi1 , and Vi2 for which Vi1 is a

convex vertex (the interior angle at the vertex is smaller than π radians), the line segment from Vi0 to Vi2 lies completely inside the polygon, and no vertices of the polygon are contained in the triangle other than the three vertices of the triangle. In the computational geometry jargon, the line segment between Vi0 and 2 Vi2 is a diagonal of the polygon. The vertex Vi1 is called the ear tip. A triangle consists of a single ear, although you can place the ear tip at any of the three vertices. A polygon of four or more sides always has at least two nono verlapping ears [