1. softmax用于计算概率分布
例如,记输入样例属于各个类别的证据为:
采用softmax函数可以将证据转化为概率:
2. cross-entropy loss用于度量两个概率分布之间的相似性
参考:知乎讲解
熵的本质是香农信息量(log(1/p))的期望。
现有关于样本集的2个概率分布p和q,其中p为真实分布,q非真实分布。按照真实分布p来衡量识别一个样本的所需要的编码长度的期望(即平均编码长度)为:
如果使用错误分布q来表示来自真实分布p的平均编码长度,则应该是:
因为用q来编码的样本来自分布p,所以期望H(p,q)中概率是p(i)。H(p,q)我们称之“交叉熵”。
注意:i的值为分布可能取值的数目,如在手写字体识别中,i=1:10;
特别的,对于二分类问题,
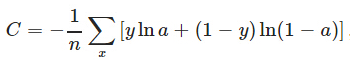
3. softmax与cross-entropy loss的关系
softmax计算概率分布a,且0 <= a<= 1。cross-entropy loss用于度量两个概率分布之间的相似性。求概率分布的方式与损失函数之间可以自由搭配,没有必然联系。
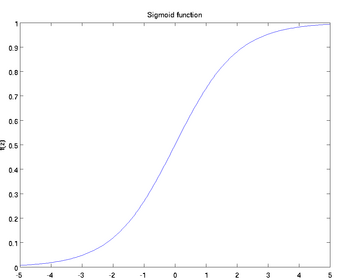
但应当注意,在人工神经网络中,当选取神经元的激活函数为sigmoid函数时,函数形式为:
对应的函数图像为:
sigmoid函数的导数满足:y’=y(1-y)
参考wphh的博客
由于神经元的激活函数选择为sigmoid函数,sigmoid函数的导数y’在两端值很小,导致参数更新会非常缓慢。如果选择普通的均方误差损失函数,会遇到上述问题。但交叉熵损失函数则可以克服这种问题。因为交叉熵损失函数的导数具有如下形式:
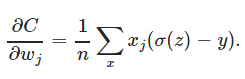
没有y’这一项,权值更新直接受σ(z)−y控制,所以收敛结果更好。
关于cross-entropy loss求导过程可参考分类问题中的交叉熵损失和均方损失









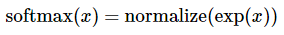
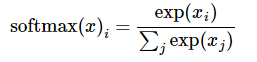


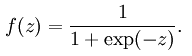
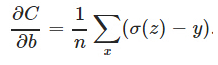














 3260
3260

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








