凸优化读书笔记01(仿射集合、仿射组合，仿射包)

克夏

已于 2023-06-27 11:18:04 修改

阅读量2.4k

点赞数 8

分类专栏：凸优化文章标签：算法

于 2021-09-23 23:16:47 首次发布

本文链接：https://blog.csdn.net/Bryant_cqc/article/details/120443480

版权

4 篇文章 8 订阅

订阅专栏

摘要：说到凸优化，免不了涉及到一个名词：凸集。顾名思义，凸集就是一个凸的集合。那么，问题来了，什么样的集合能被称为是凸的呢？在解答这个疑问之前，我们先从凸集里一个比较特殊的例子——仿射集讲起。当你理解了什么是仿射集的时候，你其实离知道什么是凸集已经不远了。

定义：如果通过集合 $C \subseteq R^n$ 中任意两个不同点的直线仍在集合 $C$ 中，那么称集合 $C$ 是仿射的。

数学表达： $\forall x_1,x_2\in C, \theta \in R,$ 有 $\theta x_1+(1-\theta)x_2 \in C.$

【注：为便于指代，将 $\theta$ 记为 $\theta_1$ ， $1-\theta$ 记为 $\theta_2$ ，即有 $\theta_1 + \theta_2 = 1$ 】

直观理解：

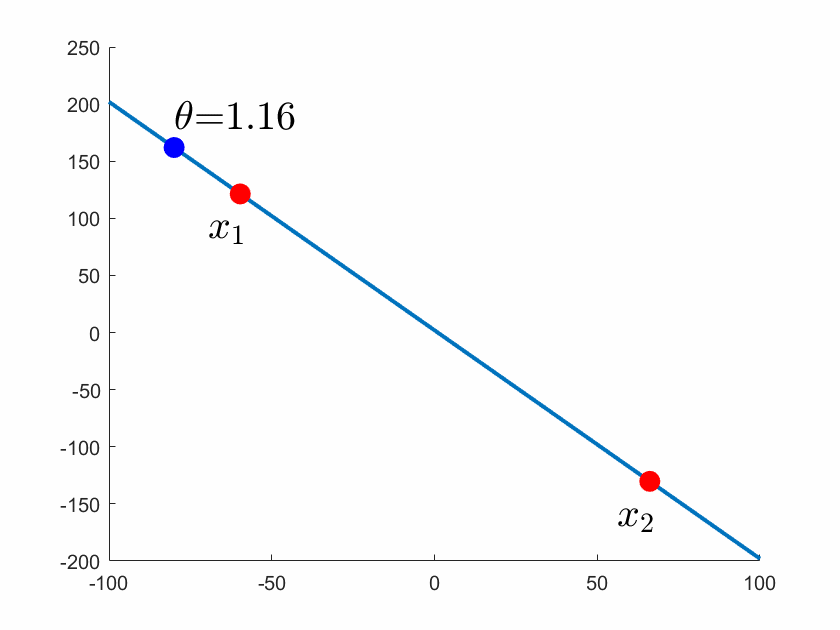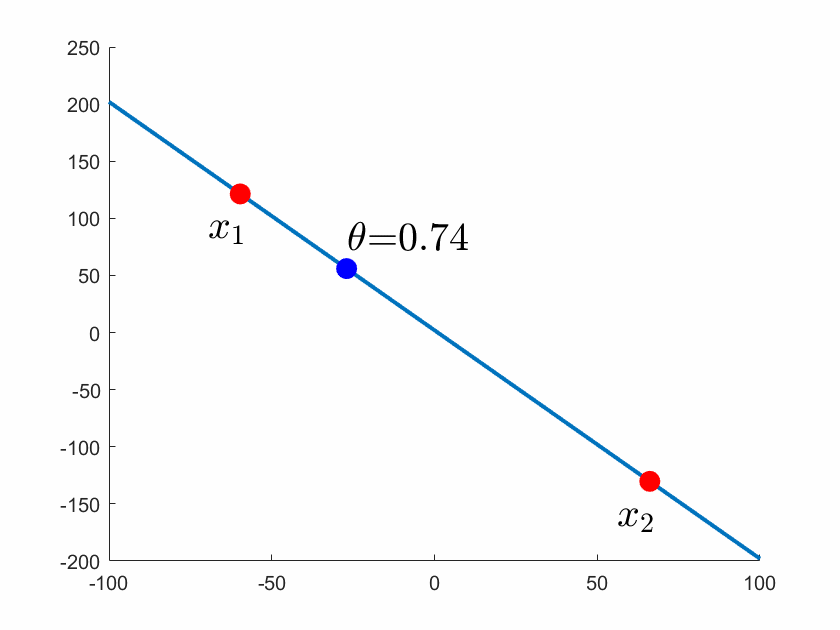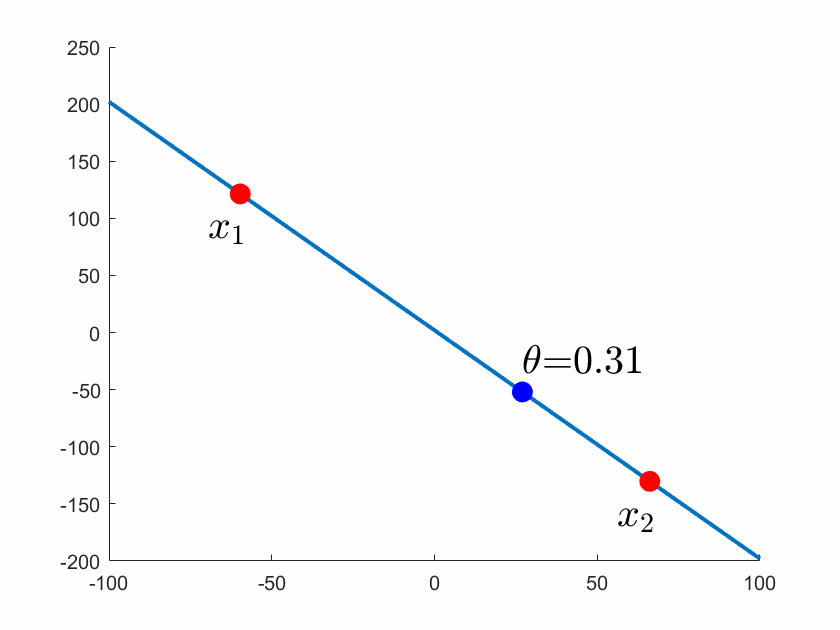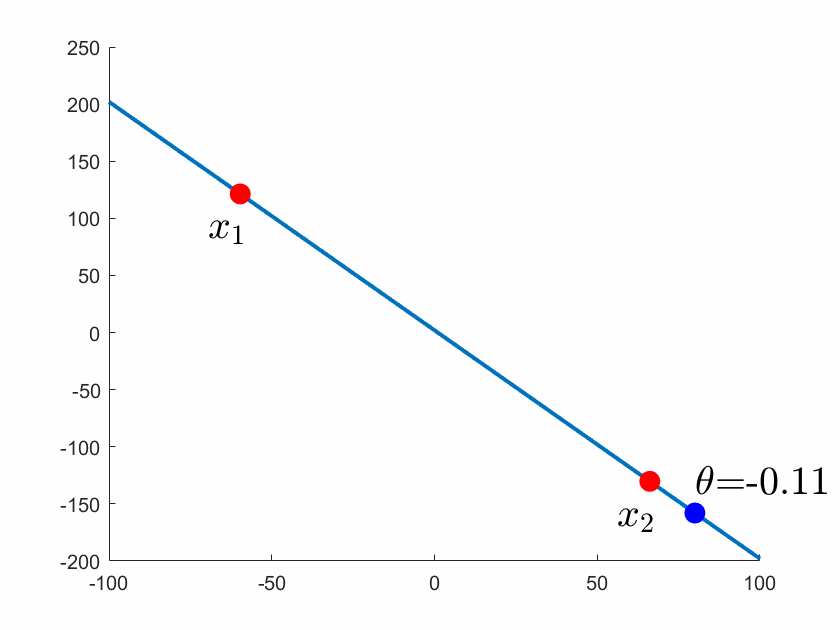
图1 通过 $x_1$ 和 $x_2$ 的直线可以参数化描述 $\theta x_1+(1-\theta)x_2$ ，其中 $\theta$ 在 $\mathbb{R}$ 上变化， $x_1$ 和 $x_2$ 之间的线段对应处于0和1之间的 $\theta$ 。

【通俗理解】打个比方，一条直线是仿射集合，因为任意两点连成的直线所有点仍在这条直线上。但是，一条线段就不是仿射集合，原因是在任意两点连成的直线上，有些点并不在线段上，不满足仿射集合的条件。将上述概念扩展到二维来说，整个二维空间才算仿射集合，局部的二维空间不算是仿射集合。

2. 仿射组合

原概念：仿射集合 $C$ 包含了 $C$ 中任意两点的系数 $\theta_1,\theta_2$ 之和为1的线性组合。

定义：若 $\theta_1+...+\theta_k=1$ ，我们称具有 $\theta_1x_1+...+\theta_kx_k=1$ 形式的点为 $x_1,...,x_k$ 的仿射组合。

归纳：一个仿射集合包含其中任意点的仿射组合，即如果集合 $C$ 是仿射集合，那么对于 $x_1,...,x_k \in C$ ，且 $\theta_1 + .. + \theta_k = 1$ ，那么 $\theta_1 x_1 + ... + \theta_k x_k$ 仍然在集合 $C$ 中。

【通俗理解】将仿射集合的原概念拓展到多个点的情况而已。

3. 仿射包

定义：集合 $C \subseteq R^n$ 里所有点的所有仿射组合组成的集合称为 $C$ 的仿射包，记为aff C。仿射包是包含集合 $C$ 的最小仿射集合。

数学表达： $\mathbf{aff} C = \begin{Bmatrix} \theta_1x_1+...+\theta_kx_k|x_1,..,x_k \in C, \theta_1+...+\theta_k=1 \end{Bmatrix}$

【通俗理解】假设集合C里有k个点，这k个点可以按照仿射组合的概念任意搭配，仿射包能够容纳给出的所有搭配。

参考文献

[美]S. Boyd, L. Vandenberghe. 凸优化[M]. 王书宁, 许鋆, 黄晓霖. 北京: 清华大学出版社, 2013.

关注