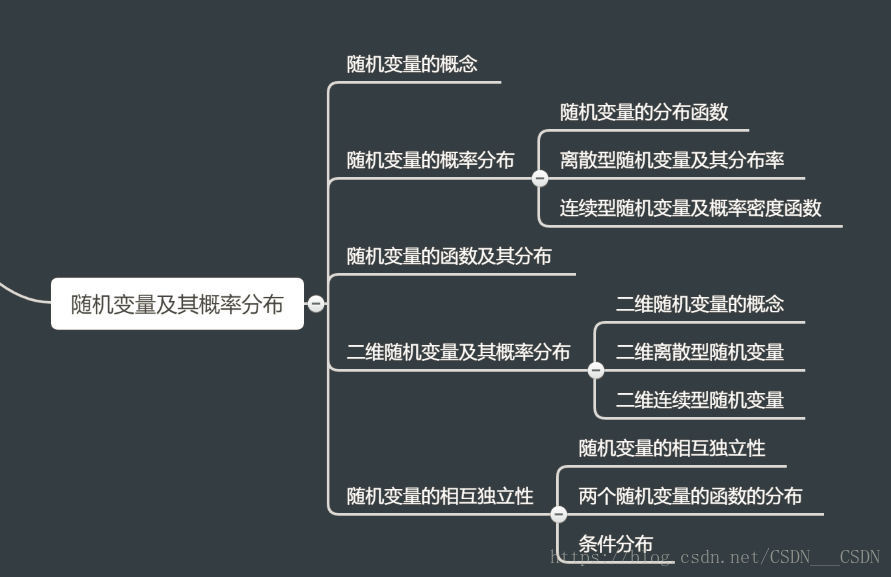
戳这里:概率论思维导图!!!
一般情况,如果随机变量Z是二维连续型随机变量(X,Y)的函数:
Z=g(X,Y)
且(X,Y)的联合概率密度函数为f(x,y),则可用以下方式求Z的分布函数:
其中 为
平面上由
所决定的区域
欢迎大家来讨论这个例题:
设二维连续型随机变量(X,Y)的联合概率密度函数为f(x,y),求 的概率密度函数
解:设Z的分布函数为,则
故Z的概率密度函数为
 这篇博客探讨了如何求解二维连续型随机变量的函数Z的分布函数,通过给出具体的例子,解释了利用联合概率密度函数求解Z的概率密度函数的方法。读者可以借此加深对概率论中随机变量函数分布的理解。
这篇博客探讨了如何求解二维连续型随机变量的函数Z的分布函数,通过给出具体的例子,解释了利用联合概率密度函数求解Z的概率密度函数的方法。读者可以借此加深对概率论中随机变量函数分布的理解。
一般情况,如果随机变量Z是二维连续型随机变量(X,Y)的函数:
Z=g(X,Y)
且(X,Y)的联合概率密度函数为f(x,y),则可用以下方式求Z的分布函数:
其中 为
平面上由
所决定的区域
欢迎大家来讨论这个例题:
设二维连续型随机变量(X,Y)的联合概率密度函数为f(x,y),求 的概率密度函数
解:设Z的分布函数为,则
故Z的概率密度函数为

 1337
1337
 1万+
1万+
 2万+
2万+
 886
886

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


