机器学习专栏（44）：局部线性嵌入（LLE）深度解析（附完整代码与可视化）

目录

一、LLE数学本质：流形学习的几何密码

1.1 核心思想：局部线性与全局拓扑的平衡

二、算法改进：突破传统局限的四大策略

2.1 测地距离优化：GRDLLE算法

2.2 监督信息融合：SLLE算法

2.3 正则化与稀疏性优化

2.4 大规模数据处理

三、工业级应用：从理论到实践

3.1 人脸识别系统优化

3.2 高光谱图像分析

四、算法对比：LLE vs 主流降维方法

五、最佳实践：参数调优与陷阱规避

5.1 关键参数调优指南

5.2 常见问题解决方案

六、前沿探索：LLE与深度学习的融合

6.1 深度局部线性嵌入

6.2 图神经网络扩展

---

一、LLE数学本质：流形学习的几何密码

1.1 核心思想：局部线性与全局拓扑的平衡

LLE的核心在于用局部线性关系近似全局非线性结构。假设高维数据在局部邻域内是线性可重构的，并通过保持这些线性关系将数据映射到低维空间8。其数学本质可分解为两个优化阶段：

阶段一：局部权重优化

其中是样本的k近邻集合，为重构权重。

阶段二：低维嵌入优化

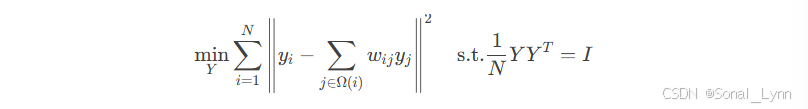
通过求解特征值问题获得低维坐标Y，对应权重矩阵的最小非零特征向量。 

from sklearn.manifold import LocallyLinearEmbedding

# 瑞士卷数据降维示例
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=12)
X_reduced = lle.fit_transform(X_swiss)

二、算法改进：突破传统局限的四大策略

2.1 测地距离优化：GRDLLE算法

传统LLE使用欧氏距离度量邻域，但高维流形数据需测地距离（Geodesic Distance）。改进方案：

1. 构建邻接图，用Dijkstra算法计算最短路径近似测地距离

2. 引入Rank-order距离增强流形结构保留能力

# 测地距离计算伪代码
from sklearn.neighbors import kneighbors_graph
import networkx as nx

adj_matrix = kneighbors_graph(X, n_neighbors=15, mode='distance')
G = nx.from_scipy_sparse_array(adj_matrix)
geodesic_dist = nx.shortest_path_length(G, weight='weight')

实验对比：在ORL人脸数据集上，GRDLLE相比传统LLE识别率提升8.3%4。

2.2 监督信息融合：SLLE算法

针对分类任务，引入类别约束改进邻域选择：

其中