从陀螺仪得到x、y、z三个角速度后就需要通过积分来得到角度,事实上,经过简单的积分是得不到正确的角度的,更得不到欧拉角,在这里说一下通过的Runge-Kunta更新四元数,从而对角速度积分得到角度的过程。
四元数能到快速的发展,得益于飞行器控制与导航的发展,要求更合理的描述刚体空间的运动,以便于计算机的计算。
在采用方向余弦描述飞行器运动时,要积分矩阵微分方程:
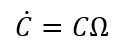
C为载体坐标到世界坐标系的方向余弦矩阵,Ω为载体坐标系相对于世界坐标系旋转角速度ω的反对称矩阵。进行计算时将包含9个一阶微分方程,计算量很大。
一、四元数求解的微分方程
在使用四元数进行求解时,需要求解四元数方程:
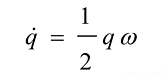
其中,q为描述载体坐标系转动的四元数,ω为载体坐标系相对世界坐标系转动的角速度,同样的可以表示为四元数:
ω=0+ωx⋅i+ωy⋅j+ωz⋅k
按四元数乘积展开:
-
q0=12(−q1⋅ωx−q2⋅ωy−q3⋅ωz)
-
q1=12(q0⋅ωx+q2⋅ωz−q3⋅ωy)
-
q2=12(q0⋅ωy−q1⋅ωz+q3⋅ωx)
-
q3=12(q0⋅ωz+q1⋅ωy−q2⋅ωx)
只需要解四个一阶微分方程。
二、Runge-Kunta法更新四元数
了解过微分方程的应该知道,只有一小部分的微分方程是可以求出通解的,剩下的大部分都需要其他的一些方法来了解性质或者求数值解等等。
Runge-Kunta法就是一种常微分方程的数值解法,可以求得常微分方程的近似数值解,可以参考《数值分析》之类的数学书籍深入了解。
这里先给出四阶标准R-K公式:
- yn+1=yn+h6(K1+2K2+2K3+K4)
- K1=f(xn,yn)
- K2=f(xn+12h,yn+12hK1)
- K3=f(xn+12h,yn+12hK2)
- K4=f(xn+h,yn+hK3)























 1287
1287

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








