Matlab:从傅里叶变换到卷积与相关，再到衍射光学、相位恢复算法

本文链接：https://blog.csdn.net/Daqiai/article/details/139738200

一、傅里叶变换类

傅里叶变换、快速傅里叶、离散傅里叶、小波、希尔伯特变换、傅里叶叠层

傅里叶变换

快速傅里叶变换FFT

信号处理之快速傅里叶变换(FFT)-通俗易懂_fft原理通俗易懂-CSDN博客

FFT（Fast Fourier Transformation），中文名快速傅里叶变换，是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。

离散傅里叶变换DFT

matlab 的fft与fft2函数完全按照DFT方式运行的。 matlab中是不会自动乘以1/N即 $\delta$ 的，留给我们自己去乘，如果单纯用于分析，可以不乘，但是要计算准确的结果，画出准确的图像则需要乘。

Matlab中fft后的频谱幅度为什么要乘以2/N？

其实除以N或除以N/2，来源于将连续的运算化为离散的运算。
积分的时候一般积分符号 $\int$ 后面的表达式是 $f(x)dx$ ，就是某个函数f(x)和自变量微分dx的乘积而写成离散求和的时候通常只写f[n]的求和，略去了与dn相乘可以遇见的是，某个函数f(x),如果我们用离散的办法去求其积分随着采样点的则加，离散的和就会增大。
实际上正确的办法是求和时要乘上采样的间隔，就是积分区间 /N 对于很多离散的积分算法，例如卷积，最后结果都要除以采样点数N才能得到正确结果。而傅立叶变化也是一种积分变换，所以得到的结果就要除以N，才是正确的。

而变换后的频谱通常将0频移到中间，分为对称的为正负频率(模对称，幅角反对称)有时表示频谱的时候只需要用其一半正频率部分就够了所以除以N之后还要乘以2，表示把正负频率的加在一起而0频的直流分量，本身在对称点，已经是正负相加过的，所以只用除以N 。

各种信号时域和频域的关系(连续对应非周期，离散对应周期)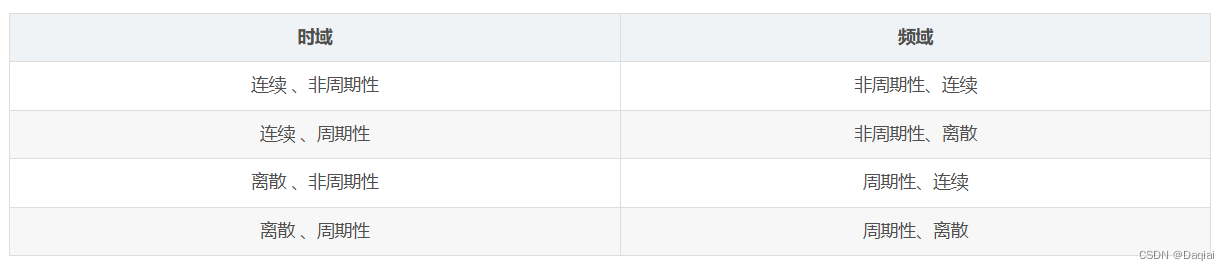

二、卷积与相关

卷积

连续型

$\displaystyle \mathrm F(\mathrm x)=\int_{-\infty}^\infty\mathrm f\displaystyle (\tau)\mathrm g(\mathrm x-\tau)\mathrm d\tau$

离散型

$\mathrm{F}\left(\mathrm{x}\right)=\sum_{\tau=0}^\mathrm{N}\mathrm{f}\left(\tau\right)\mathrm{g}\left(\mathrm{x}-\tau\right)$

Fourier convolution theorem

积定理指出，函数卷积的傅立叶变换是函数傅立叶变换的乘积。具体分为时域卷积定理和频域卷积定理，时域卷积定理即时域内的卷积对应频域内的乘积；频域卷积定理即频域内的卷积对应时域内的乘积，两者具有对偶关系。

格林函数

信号 = 源分布*点源作用的效果响应（格林函数），* 表示卷积

格林函数：对于线性算子L，在点源 $\delta$ 作用下的输出响应，就是格林函数G：LG= $\delta$

那么知道场源分布Q，就可以叠加计算出对应的输出场：L $\varphi$ =Q， $\varphi$ 为总场输出。

利用卷积的性质： $\varphi =\varphi \ast \delta=\varphi \ast (LG)=(L\varphi)\ast G=Q\ast G$

不同的线性算子对应不同的物理问题，也就对应不同性质的方程，如拉普拉斯方程、泊松方程、亥姆霍兹方程、波动方程等，都对应着不同的格林函数。

像散射介质模型里： $\triangledown ^2 G(r,r')+k^2G(r,r') = \delta (r-r')$ , $\delta (r-r')$ 表示在 $r'$ 处存在一个入射点源，所以总场：

$E(r)=\int G(r,r')E_s(r')d^3r'$

$E(r)$ 为总输出场， $E_s(r')$ 为场源。

$\triangledown ^2+k^2 \Leftrightarrow L$

$E(r)\Leftrightarrow \varphi=Q\ast G$

图像的卷积

理想图像 * 点扩散函数 = 输出图像

其中点扩散函数与传递函数互为傅里叶变换FT关系。也就是说，一个理想的点光源（脉冲δ函数来表示），经过光学系统，受衍射效应作用成为了一个光斑（脉冲相应函数impulse response来表示），那么就可以用点扩散函数来描述光学系统在这中间起到的作用，频域就是传递函数transfer function。

从空域的角度来看，一幅图像经过光学系统成像以后，由于像差和衍射的存在，肯定会退化，退化成什么样呢？就是每个点都变成了一个光斑，整幅图像就是理想图像与点扩散函数h(t)的卷积。卷积示意图和过程如下所示：

卷积这个变换有点复杂，不太直观，于是人们就想到从频域的角度来考虑问题。因为空域的卷积对应频域的乘积。一幅图像，经过光学系统成像以后，它的频谱变化为在原来的基础上乘了一个函数H(w)，H(w)是点扩散函数h(t)的傅里叶变换。H(w)就是传递函数，分为幅值和相位两部分，代表了各个频率的成分，经过光学系统以后，分别受到了不同程度的衰减和相位变化。幅值部分它影响条纹对比度的衰减，而相位部分代表条纹的移动。一般来说，我们只关注成像清晰度，这时幅值传递函数影响比相位传递函数大得多，所以我们只考虑幅值传递函数，就是我们通常说的MTF。

每单位间隔的间隔数称为空间频率（Spatial Frequency），通常以定量形式表示周期性间隔（空间周期）。空间频率的通用单位是每毫米的线对数。例如，连续的一系列黑白线对具有每对1 um的空间周期，对应的空间频率为1000线对/ mm，如图所示，间隔越小频率越高。

二者在光学设计中的作用，其实ZEMAX中专门的点扩散函数分析图，但是实际过程中用的并不是很多，因为大部分在描述光学系统成像质量的时候采用的是MTF（加畸变），也就是传递函数。这里具体说说传递函数：

假设有两个镜头，一个到30lp/mm时，MTF就降到了0.5；而另一个直到60 lp/mm时，MTF才降到0.5。那是不是就说明后者好呢？

线对越高，拍摄同一目标，得到的细节越多，那么这样说明后者比较好，因为它MTF比较好。但是这是有前提的，拍摄的目标一致，也就是视场一致。所以不能仅仅看MTF，而且不同类型镜头作用也不一致。其实更直观的理解就是单反和手机镜头，现在7P镜头动辄截止频率到了300lp/mm，而单反可能还在30lp/mm左右，但是我们常说的还是手机镜头拍出的效果能和单反媲美，也就是说还不如单反。网上找到如下一个解释，用数据说明：

“假设那个30线对的镜头是一个全幅单反上的，全幅单反的CCD大小为36*24mm，我们假设它的像素大小是1000/30/2=16微米，这样它刚好能充分利用镜头的分辨能力。1mm长度上就有60个像素，那我们的像素数就是36*60*24*60=3.1e6，310万像素；而另一个镜头呢，它是一个手机的镜头模组，我们假设感光CMOS和iPhone5S这么大吧，网上查到它的大小是1/3"，大概是4.89*3.67mm。同样假设像素大小刚好够用，1mm长度上120个像素(看了前面的文章，你应该明白再来更多的像素也没有用，镜头分辨力有限)，那么它的像素数是4.89*3.67*120*120=0.26e6，26万！！想象一下，比如有一幅画，你用单反去拍(配上前面那个镜头哦)，使之刚刚好充满视场，那这幅画会被分成310万个像素；同样的一幅画，你用手机去拍呢，只有26万个像素点。你说谁能看到的细节更多呢？”

三、衍射光学

参考来源：人类能看懂的衍射光学（含基尔霍夫衍射，瑞利--索末菲衍射，夫琅禾费衍射，角谱衍射，菲涅尔衍射积分，菲涅尔衍射的S-FFT算法,T-FFT算法,D-FFT算法）_瑞利索末菲衍射模型-CSDN博客

基尔霍夫，瑞利–索末菲公式

两者在数学上有统一的公式：

$U(x,y,d)=\frac1{j\lambda}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}U_0\left(x_0,y_0,0\right)\frac{exp(jkr)}rK(\theta)dx_0dy_0$

Fresnel approximation

$U_2(x,y)=\frac{e^{jkz}}{j\lambda z}\iint U_1(\xi,\eta)\exp\biggl\{j \frac{k}{2z}\biggl[\bigl(x-\xi\bigr)^2+\bigl(y-\eta\bigr)^2\biggr]\biggr\}d\xi d\eta$

impulse response：

$h(x,y)=\frac{e^{jkz}}{j\lambda z}\exp\biggl[\frac{jk}{2z}\biggl(x^2+y^2\biggr)\biggr]$

transfer function：

$H(f_{_X},f_{_Y})=e^{jkz}\exp\biggl[j\pi\lambda z\biggl(f_{_X}^{2}+f_{_Y}^{2}\biggr)\biggr]$

自然， $h$ 和 $H$ 互为傅里叶变换

另一个常用的形式：

$\begin{aligned} U_{2}(x,y)& =\frac{\exp(jkz)}{j\lambda z}\exp\left[ j\frac{k}{2z}\Big(x^{2}+y^{2}\Big)\right] \\ &\times\iint\left\{U_{1}(\xi,\eta)\exp\left[ j\frac{k}{2z}\Big(\xi^{2}+\eta^{2}\Big)\right]\right\}\exp\left[-j\frac{2\pi}{\lambda z}\Big(x\xi+y\eta\Big)\right] d\xi d\eta. \end{aligned}$

this expression is a Fourier transform of the source field times a chirp function where the following frequency variable substitutions are used for the transform:

$f_\zeta \rightarrow \frac{x}{\lambda z} \ f_\eta \rightarrow \frac{y}{\lambda z}$

The accuracy of the Fresnel expression when modeling scalar diffraction at close ranges suffers as a consequence of the approximations involved.By allowing a 1 rad maximum phase change,the following condition is derived:

$z^3>>\left(\frac{\pi}{4\lambda}\bigg[\left(x-\xi\right)^2+\left(y-\eta\right)^2\bigg]^2\right)_{\max}$

The criterion above provides a well-defined condition, where the Fresnel approximation can be applied with little loss of accuracy. However, for fields in the source plane with little spatial variation, such as a simple aperture back-illuminated by a plane-wave, the Fresnel approximation can provide high accuracy even when equation above is violated.

A looser criterion involves the Fresnel number, which is commonly used for determining when the Fresnel expression can be applied. The Fresnel number is given by :

$N_{F}=\frac{w^{2}}{\lambda z}$

其中 $\omega$ 是源平面中方形孔径的半宽，或圆形孔径的半径，z 是到观察平面的距离。如果给定场景的 $N_F$ 小于 $\approx$ 1，则通常认为观测平面位于菲涅耳区域，菲涅耳近似通常会导致有用的结果。然而，对于源孔径上相对“平滑”的场，菲涅耳表达式可以适用于甚至 20 或 30 的菲涅耳数。在几何光学环境中，菲涅耳表达式描述了近轴假设下的衍射，其中仅考虑相对于光轴形成小角度（<~0.1 rad）的光线。

Fraunhofer approximation

$\begin{aligned}U_{2}(x_{2},y_{2})&=\frac{\exp(jkz)}{j\lambda z}\exp\biggl[j\frac{k}{2z}\biggl(x^{2}+y^{2}\biggr)\biggr]\\&\times\iint U_{1}(\xi,\eta)\exp\biggl[-j\frac{2\pi}{\lambda z}\bigl(x\xi+y\eta\bigr)\biggr]d\xi d\eta.\end{aligned}$

Along with multiplicative factors out front, the Fraunhofer expression can be recognized simply as a Fourier transform of the source field with the variable substitutions

$f_\zeta \rightarrow \frac{x}{\lambda z} \ f_\eta \rightarrow \frac{y}{\lambda z}$

This condition requires very long propagation distances relative to the source support size. However, a form of the Fraunhofer pattern also appears in the propagation analysis involving lenses. The Fraunhofer diffraction expression is a powerful tool and finds use in many applications such as laser beam propagation, image analysis, and spectroscopy.

The Fraunhofer expression cannot be written as a convolution integral, so there is no impulse response or transfer function. But, since it is a scaled version of the Fourier transform of the initial field, it can be relatively easy to calculate.

And as with the Fresnel expression, the Fraunhofer approximation is often used with success in situations where $z>>\left(\frac{k(\xi^2+\eta^2)}{2}\right)_{\max}$ is not satisfied. For simple source structures such as a plane-wave illuminated aperture, the Fraunhofer result can be useful even when $z>>\left(\frac{k(\xi^2+\eta^2)}{2}\right)_{\max}$ is violated by more than a factor of 10, particularly if the main quantity of interest is the irradiance pattern at the receiving plane. Using the Fresnel number $N_F$ the commonly accepted requirement for the Fraunhofer region is $N_F<<1$ .