学习贝叶斯滤波笔记

最近在学习粒子滤波和贝叶斯滤波，在实现代码之前，肯定要先搞懂这两个东西是干什么用的？它们在现实生活中能解决什么问题？以及怎么实现的？
找的几篇文章，这几篇文章我觉得写的很通俗易懂，在这里感谢一下文章的作者：
《[易懂实例讲解]离散型贝叶斯滤波python编程代码实践》
《理解与推导贝叶斯滤波(Bayes Filter)算法》
《贝叶斯滤波的应用场景举例》
作者：白巧克力亦唯心 《滤波估计理论（一）——贝叶斯滤波》
什么是filtering问题？：就是说已知前t个观测值，求t时刻的系统状态，即求解$P(z_t|x_1,x_2,...x_t)$

知识准备：

对一个估计问题的建模：

状态空间模型:

假设现在有一个机器人，机器人上安装了GPS等设备来跟踪机器人的当前位置，并且获取当前位置的测量信息（比如说这个机器人离周围的建筑的距离有多远等等），记为$z_k$，同时我们使用遥控器控制机器人移动的时候还会获得控制信息$u_k$(比如说，走了多久，速度是多少，是朝什么方向)。然后我们对机器人当前位置的预测记为$x_k$,那么用数学模型来描述就是$$x_k=f(x_{k-1},u_k)+w_k$$ $$z_k=h(x_k)+v_k$$
该模型是一个典型的状态空间模型，上下两式分别成为状态空间的状态方程和测量方程。

概率模型：

现在从概率方面考虑机器人位置的问题，在现实生活中，我们通过各种设备获取的信息根实际的数值是有误差的（比如说我控制机器人向前以1m/秒的速度走5秒，但是实际中，可能由于轮子打滑等问题，机器人走的距离实际没有5米，这是预测上的误差。再比如，我用机器人上的摄像头和GPS测量出机器人距离周围建筑的距离根实际的距离也是有差别的，这是测量上的误差），但是机器人一定在真实值的一定范围内。于是，我们就可以假设预测信息和测量信息都服从一定的概率分布，来表征两个信息值在真实值附近的概率分布，同时，我们现在可以拥有的信息包括前k-1时刻的预测和量测，因此k时刻的预测信息和量测信息本质上是一个条件概率模型：$$x_k\sim p(x_k\mid x_{0:k-1},z_{1:k-1})$$$$z_k\sim p(y_k\mid x_{0:k},z_{1:k-1})$$

状态空间模型

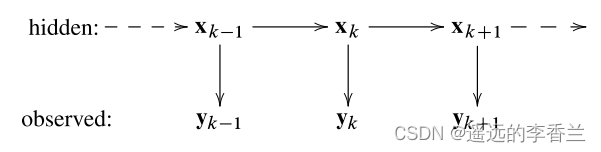
图中的hidden就是指机器人的状态量（就是机器人的位置），observed就是我们的观测量（通过各种设备观测出来的）。
隐马尔科夫模型的两个性质：
1.状态量的马尔科夫性：就是说在给定了k-1时刻的状态量$x_{k-1}$的情况下，k时刻的状态量$x_k$只与$x_{k-1}$有关，与其他的状态量都无关。
2.观测量的条件独立性：在给定当前状态量$x_k$的条件下，则当前观测量只与$x_k$有关，与其他的历史状态量和观测量都无关。
由以上两条性质我们可以将条件概率模型简化成如下：$$x_k\sim p(x_k\mid x_{k-1})$$$$z_k\sim p(z_k\mid x_k)$$
说明白了其实预测的过程就是根据之前已有的观测值来估计出当前的状态值得过程

状态估计领域常见三个名词：预测（prediction），滤波（filtering）和平滑（smoothing）。

滤波分布(filtering distribution):在给定当前和之前量测信息$z_{1:k}$条件下，当前状态$x_k$ 的边缘分布$p(x_k|z_{1:k})$
预测分布(prediction distribution):在给定当前和之前量测信息$z_{1:k}$条件下，未来状态$x_{k+n}$的边缘分布$p(x_k|z_{1:k})$
平滑分布(smoothing distribution):在给定量测区间$z_{1:T}$的条件下，当前状态$x_k$的边缘分布$p(x_k|z_{1:T})$ ,其中T>K

介绍一下贝叶斯:贝叶斯法则
通常，事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件下的概率是不一样的；然而，这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
贝叶斯法则是关于随机事件A和B的条件概率和边缘概率的。 公式如下
$$P(A_i|B)=\frac{P(B|A_i)P(A_i)}{{\sum }_{j}P(B|A_j)P(A_j)}$$
在贝叶斯法则中，

1. P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
2. P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
3. P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
4. P(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）

贝叶斯滤波的作用：

贝叶斯滤波算法的工作就是根据已有的信息来计算某件事发生的概率 ，比如我要判断一个人的性别，我首先给了几个信息：短头发，没有涂口红。然后根据这些信息来判断这个人的性别，如果有新的信息，那么就会重新计算概率。更新概率值的方法是根据概率论中的条件概率计算公式来更新的。也即是说从贝叶斯理论的观点来看，状态估计问题（目标跟踪、信号滤波）就是根据之前一系列的已有数据$y_{1:k}$递推的计算出当前状态$x_k$的可信度。这个可信度就是概率公式$p(x_k|y_{1:k})$它需要通过预测和更新两个步奏来递推的计算。预测过程是利用系统模型(状态方程1)预测状态的先验概率密度，也就是通过已有的先验知识对未来的状态进行猜测，更新过程则利用最新的测量值对先验概率密度进行修正，得到后验概率密度，也就是对之前的猜测进行修正。
先来看看预测： 由上一时刻的概率密度$p(x_{k-1}|y_{1:k-1})$得到$p(x_k|y_{1:k-1})$（从上面的动态模型图来看就是已知观测值前k-1个观测值$y_{1:k-1}$，然后去求$x_k$的系统状态，这里的预测值就是$x_t$的先验）
计算推导如下：前两个等式，就是我们想建立$x_t和x_{t-1}$之间的联系，于是把$x_{t-1}引入公式$
，第二个等式到第三个等式就是使用了齐次Markov假设（即假设$x_k$只与$x_{k-1}$有关 ）
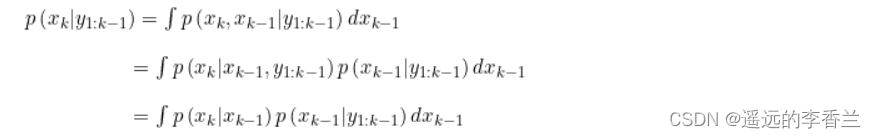更新：由$p(x_k|y_{1:k-1})$得到后验概率$p(x_k|y_{1:k})$，这里的跟新是指我们已经得到了k时刻的测量值了，现在需要对上一步的预测值进行跟新修正，这就是滤波了（从动态模型图来看就是，此时已经从t-1时刻来到了t时刻，t时刻我们就会知道此时的观测值$y_k$,这个时候我们就要对之前的预测值进行更正或者跟新，跟新后的值就是$x_t$的后验）。这里的后验概率也将作为下次的预测，逐渐递推。
计算推导：

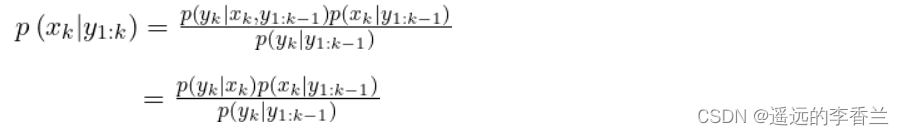
实现过程

当我什么信息都不给的时候，这个时候我只设置了初始值，比如说男性的概率是0.5，女性的概率是0.5。但是当我告诉贝叶斯算法这个人是短头发，然后贝叶斯就会重新计算性别概率。比如说，我已经知道如下信息：
短头发的人中男性占比：0.8。
不使用口红的人中男性占比：0.9
这两个信息就是先验知识，这是我们已经通过数据统计出来的。正如之前说的，如果我们没有这些信息，那么我们让贝叶斯判定性别时，贝叶斯就会根据我们设定的初始值来判定。现在我们给了新的信息，贝叶斯又是如何来跟新概率的呢？
这个人是短头发的条件下是男性的概率可以用$P(男|短发)$来表示。在最先的时候我们在先验知识中已经告诉了短发中男性的占比为0.8，但是这个值是怎么来的呢？根据概率论知识我们可以知道$$P(男|短发)=\frac{P(男生并且留短发)}{P(留短发)}=\frac{P(短发|男)P(男)}{P(短发)}$$从这个公式我们就可以看出来，只要我们知道了$P(男生并且留短发)$、$P(留短发)$或者知道了$P(短发|男)、P(男)、P(短发)$，我们就可以算出$P(男|短发)$的概率，在现实生活中，哪些先验知识容易获得就可以使用对应的公式进行计算。对于这里而言，贝叶斯公式通常使用$P(男|短发)=\frac{P(短发|男)P(男)}{P(短发)}$这个方式。到这里有关于贝叶斯滤波的介绍就告一段落。接下来尝试理解数学公式推导。

举个例子（python实现）

我们举一个机器人走路的问题，现有一个机器人，站在初始点，我们对机器人发送9次前进的命令，机器人有20%的概率不执行，有50%的概率向前走一米，有30%的概率向前走2米。问机器人在个位置的概率是多少？
这里给出执行前两次命令的过程：

之后的步骤就照着第二步这样走下去，注意在所有位置的概率之和要为1.