【考研数学】高等数学第三模块——积分学 | Part II 定积分（一般性质及特殊性质）

前言

上文说到了定积分部分的定义，现在继续从定积分的基本性质开始。

二、定积分及其应用

2.2 定积分的一般性质

性质 1 —— 设 $f(x),g(x)$ 为区间 $[a,b]$ 上的可积函数， $k_1,k_2$ 为常数，则 $${\int }_a^b[k_{1}f(x)+k_{2}g(x)]dx=k_1{\int }_a^{b}f(x)dx+k_2{\int }_a^{b}g(x)dx.$$

即常数可以提到积分外面去；积分具有可加性。

性质 2 —— 设 $f(x)$ 为可积函数，则 $${\int }_a^{b}f(x)dx={\int }_a^{c}f(x)dx+{\int }_c^{b}f(x)dx.$$

即积分的区间可以进行拆成多个小区间相加。

性质 3 —— 关于积分的比较性质：
（1）设 $f(x)$ 在区间 $[a,b]$ 上可积且 $f(x)\ge 0$ ，则 ${\int }_a^{b}f(x)dx\ge 0;$
（2）设 $f(x),g(x)$ 为区间 $[a,b]$ 上的可积函数且 $f(x)\ge g(x)$ ，则 ${\int }_a^{b}f(x)dx\ge {\int }_a^{b}g(x)dx;$
（3）设 $f(x)$ 以及 $|f(x)|$ 在区间 $[a,b]$ 上可积，则 $$|{\int }_a^{b}f(x)dx|\ge {\int }_a^b|f(x)|dx.$$
性质5——（积分中值定理） $f(x)$ 是 $[a,b]$ 上的连续函数，则存在 $\xi \in [a,b]$ ，使得：$${\int }_a^{b}f(x)dx=f(\xi )(b-a).$$ 证明：利用介值定理进行证明：

因为 $f(x)$ 连续，所以在区间 $[a,b]$ 上存在最小值 $m$ 和最大值 $M$ ，有 $m\le f(x)\le M$ ，两边同时积分，有 $m(b-a)\le {\int }_a^{b}f(x)\le M(b-a)$ ，即：$$m\le \frac{1}{b-a}{\int }_a^{b}f(x)dx\le M$$ 由介值定理，可知原命题得证。

$\frac{1}{b-a}{\int }_a^{b}f(x)dx$ 也称为函数在该区间的平均值。

积分中值定理的中值 $\xi$ 为闭区间，有些时候无法证明应用去证明开区间的结论，因此有如下推广。

定理 1 —— 积分中值定理推广 设$f(x)$ 是 $[a,b]$ 上的连续函数，则存在 $\xi \in (a,b)$ ，使得：$${\int }_a^{b}f(x)dx=f(\xi )(b-a).$$ 证明：利用拉氏定理证明：

记 $F(x)={\int }_a^{x}f(x)dx$ ，$f(x)$ 为连续函数（可积），故原函数 $F(x)$ 可导且 $F^{\prime }(x)=f(x).$
由拉氏定理，存在 $\xi \in (a,b)$ ，使得 ${\int }_a^{b}f(x)dx=F(b)-F(a)=F^{\prime }(\xi )(b-a)$ ，$F^{\prime }(\xi )=f(\xi )$ ，故原命题得证。

定理 2 —— 积分第一中值定理 设 $f(x),g(x)$ 为区间 $[a,b]$ 上的连续函数，且 $g(x)\ge 0$ ，则存在 $\xi \in [a,b]$ ，使得 ${\int }_a^{b}f(x)g(x)dx=f(\xi ){\int }_a^{b}g(x)dx.$

即可以把没有确定符号的函数提出来，出现两个函数相乘时的积分可以考虑。

证明： 由连续，可知 $f(x)$ 有 $m\le f(x)\le M$ ，因为 $g(x)\ge 0$ ，则 $mg(x)\le f(x)g(x)\le Mg(x)$ ，同时积分，有 $m{\int }_a^{b}g(x)dx\le {\int }_a^{b}f(x)g(x)dx\le M{\int }_a^{b}g(x)dx.$

（1）$g(x)=0$ ，则 ${\int }_a^{b}g(x)dx=0$ ，则 $\forall \xi \in [a,b]$ ，原命题都成立。
（2）$g(x)>0$ ，不等式同时除以 ${\int }_a^{b}g(x)dx$ ，则有 $$m\le \frac{{\int }_a^{b}f(x)g(x)dx}{{\int }_a^{b}g(x)dx}\le M$$ 根据介值定理，存在 $\xi \in [a,b]$ ，使得 $m\le f(\xi )\le M$ ，故原命题得证。

✨定理 3 —— 分别是判断符号的三个小定理，在证明积分不等式时比较重要。

定理 4 —— （柯西不等式） 设 $f(x),g(x)$ 在 $[a,b]$ 上连续，则有：$$({\int }_a^{b}f(x)g(x)dx{)}^2\le {\int }_a^b{f}^2(x)dx{\int }_a^b{g}^2(x)dx.$$

证明：对任意的 $t\in R$ ，有 $[tf(x)+g(x){]}^2\ge 0$ ，展开即 $f^2(x)t^2+2f(x)g(x)t+g^2(x)\ge 0$ ，两边在 $[a,b]$ 上积分有：$$[{\int }_a^b{f}^2(x)dx]t^2+[2{\int }_a^{b}f(x)g(x)dx]t+{\int }_a^b{g}^2(x)dx\ge 0.$$ 定积分均为一个常数，因此上式可看作一个关于 $t$ 的一元二次方程。
（1）若 ${\int }_a^b{f}^2(x)dx=0$ ，根据定理 3 ，可得到 $f(x)\equiv 0$ ，原命题成立。
（2）若 ${\int }_a^b{f}^2(x)dx>0$ ，可知该一元二次方程的函数图像开口朝上，若要满足非负，则判别式应满足 $$\Delta =4[{\int }_a^{b}f(x)g(x)dx{]}^2-4{\int }_a^b{f}^2(x)dx{\int }_a^b{g}^2(x)dx\le 0$$ 整理后，即可得到原命题。

2.3 定积分的特殊性质

2.3.1 ✨对称区间上定积分性质

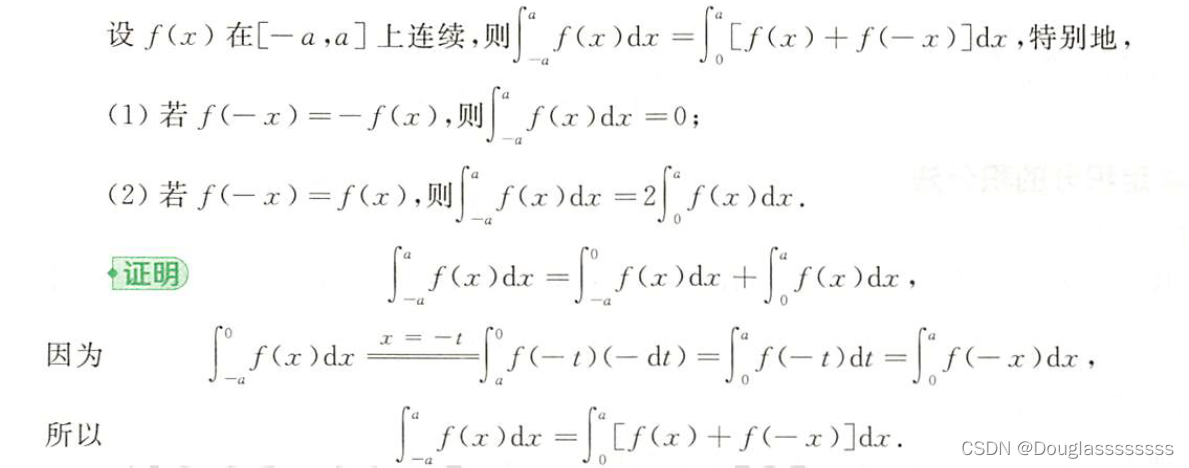
当出现对称区间或者可以构造对称区间时，应想到利用这条性质，有时可发挥奇效。如计算下面的积分： $$I={\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{si{n}^{4}x}{1+e^x}dx.$$ 不利用这个性质感觉根本下不了手。$$I={\int }_0^{\frac{\pi }{2}}(\frac{si{n}^{4}x}{1+e^x}+\frac{si{n}^{4}x}{1+e^{-x}})dx={\int }_0^{\frac{\pi }{2}}si{n}^{4}xdx=\frac{3}{4}\frac{1}{2}\frac{\pi }{2}=\frac{3\pi }{16}$$

2.3.2 ✨三角函数定积分的性质

（1）设 $f(x)\in C[a,b]$ ，则 $${\int }_0^{\frac{\pi }{2}}f(sinx)dx={\int }_0^{\frac{\pi }{2}}f(cosx)dx$$

也就是在 $[0,\frac{\pi }{2}]$ 区间的积分中，$sinx$ 可以和 $cosx$ 相互调换位置，有时可发挥奇效。

其证明过程如下：
令 $x+t=\frac{\pi }{2}$ ，则 $${\int }_0^{\frac{\pi }{2}}f(sinx)dx={\int }_0^{\frac{\pi }{2}}f(sin(\frac{\pi }{2}-t)dt={\int }_0^{\frac{\pi }{2}}f(cosx)dx$$
证毕。

特别地，有 $$I_n={\int }_0^{\frac{\pi }{2}}f(sinx)dx={\int }_0^{\frac{\pi }{2}}f(cosx)dx=\frac{n-1}{n}{I}_{n-2}$$ 且 $I_0=\frac{\pi }{2},I_1=1.$

因此，以后若碰见 0 到 $\frac{\pi }{2}$ 区间上只有 $sin,cos$ 的高次幂，可以直接写出答案。如 $${\int }_0^{\frac{\pi }{2}}si{n}^{4}xdx=\frac{3}{4}\frac{1}{2}{I}_0=\frac{3\pi }{16}$$ 另外补充，区间是 $[0,\pi ]$ 时，$\sin$ 不分奇偶次，不过需要乘个 2 ；$\cos$ 的次数如果是偶数，同 $\sin$ ，但如果是奇数，结果是 0 ；区间是 $[0,2\pi ]$ 时，分奇偶，奇数次为 0 ，偶数次需要多乘一个 4 。

（2）设 $f(x)$ 在 $[0,1]$ 上连续，则 $${\int }_0^{\pi }f(sinx)dx=2{\int }_0^{\frac{\pi }{2}}f(sinx)dx$$ 即有：$${\int }_0^{\frac{\pi }{2}}f(sinx)dx={\int }_{\frac{\pi }{2}}^{\pi }f(sinx)dx.$$ 证明如下：$${\int }_0^{\pi }f(sinx)dx={\int }_0^{\frac{\pi }{2}}f(sinx)dx+{\int }_{\frac{\pi }{2}}^{\pi }f(sinx)dx$$ 令 $x-\frac{\pi }{2}=t$ ，则${\int }_{\frac{\pi }{2}}^{\pi }f(sinx)dx={\int }_0^{\frac{\pi }{2}}f(cost)dt={\int }_0^{\frac{\pi }{2}}f(sinx)dx.$
证毕。

这样化成了 $[0,\frac{\pi }{2}]$ 区间上，碰上高次幂就可以用前面那个结论了。

（3）设 $f(x)$ 在 $[0,1]$ 上连续，则 $${\int }_0^{\pi }xf(sinx)dx=\frac{\pi }{2}{\int }_0^{\pi }f(sinx)dx=\pi {\int }_0^{\frac{\pi }{2}}f(sinx)dx$$

有了这个结论，即便前面有 $x$ 碍事，一样可以把它去掉，变成 $[0,\frac{\pi }{2}]$ 范围内的积分。

此结论原理如下：
令 $x+t=\pi$ ，则：$$I={\int }_0^{\pi }xf(sinx)dx={\int }_0^{\pi }(\pi -t)f(sint)dt={\int }_0^{\pi }\pi f(sinx)dx-I$$ $$2I=\pi {\int }_0^{\pi }f(sinx)dx$$ 两边除以 2 ，则原命题得证。

如果式子较为复杂，有很多干扰项，不知道是不是能直接去掉 $x$ ，最好就自己用这个 $x+t=\pi$ 代换，自己推一下。

（4）如果是一整个周期 $2\pi$ ，需要加上绝对值。

2.3.3 周期函数定积分的性质

写在最后

关于积分法我感觉更多是题目实战了，不多赘述。定积分还有广义积分和应用，放在后面吧。