二项分布 Binomial Distribution

• Bernouilli 随机变量：

  • 定义：
    • An individual trial has only two possible outcomes.
    • 一个实验只有两个可能的结果，分别定义为成功(success)和失败(failure)。

• 二项分布 Binomial Distribution:

  • 定义：
    • the probability of having exactly k successes in n independent Bernouilli trials with probability of success p。
    • 描述了在n次独立的Bernouilli实验中恰好有k次成功的概率，且每次实验成功概率均为p。
  • 
    • # of scenarios * P(single scenario)
  • 条件：
    • 每次Bernouilli实验是相互独立的 Independent
    • 实验的个数n是固定的
    • 每次实验的结果要被分成成功或者失败中的一个
    • 每次实验成功的概率必须相同
    • 我们对n次中成功的次数(Y)感兴趣
  • 二项分布的期望值和标准差：
    • 
    • 
  • 计算的两种方法：
    • 代入公式
    • 使用R语言
      • 这里的例子是一共十次实验，每次成功的概率是0.13，求正好成功8次的概率：

      • dbinom(8, size = 10, p = 0.13)

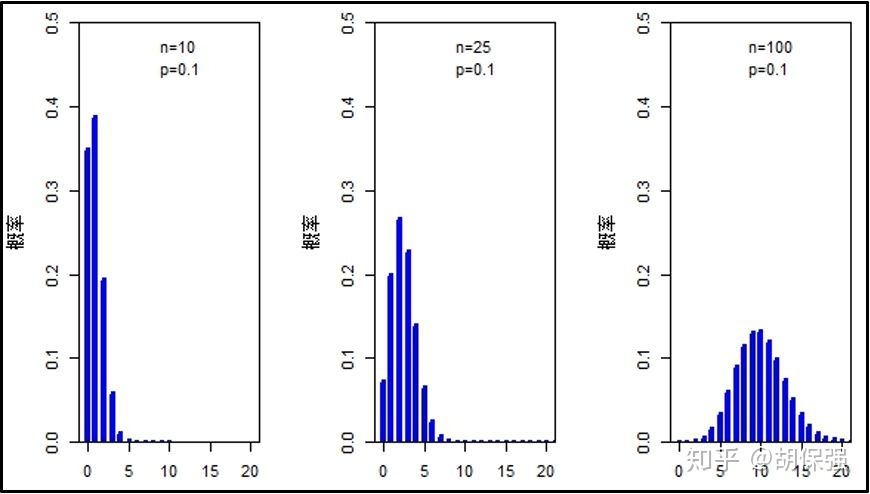
• 正态近似 Normal approximation to binomial

  

  图片来源： 如何理解正态分布作为二项分布和泊松分布的近似？ - 知乎 (zhihu.com)

  • 当n足够大时（有至少10个成功和10个失败），那么该二项分布的形状就很接近一个正态分布。
    • 
    • 
    • 上述两个条件通过后，可用以下公式进行估算：
      • ，其中， 。

以下是Duke Coursera笔记，持续更新。