【时间序列预测】Autoformer论文笔记

文章全名：Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting

文章链接：proceedings.neurips.cc/paper_files/paper/2021/file/bcc0d400288793e8bdcd7c19a8ac0c2b-Paper.pdf

文章来源：NeurIPS 2021

完成单位：清华大学软件学院

摘要

本文研究了长距离时序预测问题。

长距离时序预测的复杂的时间模式让模型很难学习到可靠的依赖关系。

另外由于Transformer的计算量太大，所以对于大量的时序数据只能采用稀疏版的点级别自注意力，导致了信息利用的瓶颈。

本文设计了Autoformer，它是一种新的分解结构，有着一种自关联机制。

这种设计赋予了Autoformer对于复杂时间序列的渐进分解能力

此外，受到随机过程理论的启发，本文基于序列的周期性设计了自相关机制，它在子序列级别上进行依赖关系的发现和表示聚合。

实验发现，自相关比自注意力的准确性更高，在长期预测中在六个benchmark都达到了最好表现。

简介

首先本文介绍了Transformer在建模长距离序列数据依赖的优越性。

然后又根据预测任务对信息挖掘的高要求这一挑战，总结了Transformer在长时序预测的问题。

一是长距离序列数据本身的依赖关系会被复杂的时间模式所掩盖

二是计算复杂度太高，因为数据序列很长，所以point-wise的self-attention计算量很大，有些文献也提出了稀疏注意的方法，但因为稀疏注意仍然还是点级别表示聚合，所以就会牺牲一部分信息没有被利用。

为了更好地理解这种错综复杂的时间模式，本文尝试使用分解这一思想来进行时间序列分析，它可以处理复杂的时间序列并且提取出一些更好预测的成分。

但是根据预测任务的性质，这种分解只能应用于过去序列的预处理，因为未来是未知的。这种方式就限制了分解的作用，忽略了各分解部分对未来的潜在交互。因此本文提出了一种通用的框架，让深度预测模型有着渐进分解的能力。

分解可以解开时间序列的复杂关系，突出显示时间序列的固有特性。受此启发本文尝试利用序列所蕴含的周期性规律来重构自注意力中点级别的注意。本文发现不同时间段相同位置的子序列有着相似的时间过程。因此本文就尝试构建一种序列级别的关联。

模型

本文提出了Autoformer作为分解结构，并设计了一种自关联机制来发掘不同时间段的子序列之间的相似性，而不是时间点，这样既可以提升时间效率也能够提升信息利用率。

模型的整体结构如下：

分解结构

本文使用了分解的思想，可以将时间序列分解为趋势-周期性部分和季节性部分。这两部分分别反映了序列的长期发展趋势和季节性。然而，直接进行分解对于未来的系列是不可实现的，因为未来是未知的。为了解决这个困境，本文在Autoformer中引入了一个序列分解块作为内部操作，可以从预测的中间隐藏变量中逐步提取长期的稳定趋势。具体而言，本文采用移动平均法来平滑周期性波动，并突出长期趋势。
$$\begin{array}{rl}& {\mathcal{X}}_{\mathrm{t}}=\mathrm{AvgPool}(\mathrm{Padding}(\mathcal{X}))\\ & {\mathcal{X}}_{\mathrm{s}}=\mathcal{X}-{\mathcal{X}}_{\mathrm{t}},\end{array}$$
$\mathcal{X}$的维度是L * d，L是序列的长度，${\mathcal{X}}_t$表示提取出来的趋势周期性特征，${\mathcal{X}}_s$表示提取出的季节性特征。${\mathcal{X}}_t,{\mathcal{X}}_s=SeriesDecomp(\mathcal{X})$，也就是网络结构中的Series Decomp。

模型输入

encoder的输入是过去$I$个时间步的数据，解码器的输入包含了季节性部分${\mathcal{X}}_{des}\in {\mathbb{R}}^{(\frac{I}{2}+O)\times d}$和趋势周期性部分${\mathcal{X}}_{det}\in {\mathbb{R}}^{(\frac{I}{2}+O)\times d}$，$O$表示预测序列长度。

decoder输入初始化包含了两个部分，一部分是encoder输入序列后半部分$\left({\mathcal{X}}_{\text{en }\frac{1}{2}:I}\right)$的分解结果，一部分是长度为$O$的占位符。
$$\begin{array}{rl}{\mathcal{X}}_{\text{ens }},{\mathcal{X}}_{\text{ent }}& =\mathrm{SeriesDecomp}\left({\mathcal{X}}_{\text{en }\frac{1}{2}:I}\right)\\ {\mathcal{X}}_{\text{des }}& =\mathrm{Concat}\left({\mathcal{X}}_{\text{ens }},{\mathcal{X}}_0\right)\\ {\mathcal{X}}_{\text{det }}& =\mathrm{Concat}\left({\mathcal{X}}_{\text{ent }},{\mathcal{X}}_{\text{Mean }}\right)\end{array}$$
其中${\mathcal{X}}_0$表示全部填充为0，${\mathcal{X}}_{Mean}$表示全部填充为编码器输入的平均值。

编码器

编码器主要关注于季节性特征建模，编码器输出包含了过去的季节性信息并且会作为交叉信息来帮助解码器修正预测结果。编码器的计算公式如下：
$$\begin{array}{rl}& {\mathcal{S}}_{\mathrm{en}}^{l,1}{}_{-}=\mathrm{SeriesDecomp}\left(\text{ Auto-Correlation }\left({\mathcal{X}}_{\mathrm{en}}^{l-1}\right)+{\mathcal{X}}_{\mathrm{en}}^{l-1}\right)\\ & {\mathcal{S}}_{\mathrm{en}}^{l,2}{}_{-}=\mathrm{SeriesDecomp}\left(\text{ FeedForward }\left({\mathcal{S}}_{\mathrm{en}}^{l,1}\right)+{\mathcal{S}}_{\mathrm{en}}^{l,1}\right)\end{array}$$
其中，"_"表示被删除的趋势部分，因为编码器重点关注的是季节性的信息，1和2分别表示auto-correlation和feedforward的输出结果。第$l$层编码层的输出就是 ${\mathcal{S}}_{en}^{l,2}$。

解码器

解码器包含了两个部分，分别是处理趋势周期性元素的累计结构${\mathcal{T}}_{de}^l$和处理季节性元素的堆叠自相关结构${\mathcal{S}}_{de}^l$。每个解码器都包含了内置的自相关结构（第一块），以及和编码器联动的自相关结构（第二块），这样的话可以修正预测结果，也可以利用上过去的季节性信息。模型在解码器期间从中间隐藏变量中提取潜在趋势，使Autoformer能够逐步改进趋势预测并消除在自相关阶段发掘基于时间段的依赖关系时可能存在的干扰信息。
$$\begin{array}{rl}{\mathcal{S}}_{\mathrm{de}}^{l,1},{\mathcal{T}}_{\mathrm{de}}^{l,1}& =\mathrm{SeriesDecomp}\left(\text{ Auto-Correlation }\left({\mathcal{X}}_{\mathrm{de}}^{l-1}\right)+{\mathcal{X}}_{\mathrm{de}}^{l-1}\right)\\ {\mathcal{S}}_{\mathrm{de}}^{l,2},{\mathcal{T}}_{\mathrm{de}}^{l,2}& =\mathrm{SeriesDecomp}\left(\text{ Auto-Correlation }\left({\mathcal{S}}_{\mathrm{de}}^{l,1},{\mathcal{X}}_{\mathrm{en}}^N\right)+{\mathcal{S}}_{\mathrm{de}}^{l,1}\right)\\ {\mathcal{S}}_{\mathrm{de}}^{l,3},{\mathcal{T}}_{\mathrm{de}}^{l,3}& =\mathrm{SeriesDecomp}\left(\text{ FeedForward }\left({\mathcal{S}}_{\mathrm{de}}^{l,2}\right)+{\mathcal{S}}_{\mathrm{de}}^{l,2}\right)\\ {\mathcal{T}}_{\mathrm{de}}^l& ={\mathcal{T}}_{\mathrm{de}}^{l-1}+{\mathcal{W}}_{l,1}\ast {\mathcal{T}}_{\mathrm{de}}^{l,1}+{\mathcal{W}}_{l,2}\ast {\mathcal{T}}_{\mathrm{de}}^{l,2}+{\mathcal{W}}_{l,3}\ast {\mathcal{T}}_{\mathrm{de}}^{l,3},\end{array}$$
其中${\mathcal{X}}_{de}^l={\mathcal{S}}_{de}^{l,3}$，也就是decoder的输出是最后一层输出的季节性信息

最终的预测输出就是两个分解模块的和。
$$Prediction={\mathcal{W}}_{\mathcal{S}}\ast {\mathcal{X}}_{\mathrm{de}}^M+{\mathcal{T}}_{\mathrm{de}}^M$$
$M$是decoder里layer的数量，${\mathcal{W}}_{\mathcal{S}}$的目的是将季节性元素${\mathcal{X}}_{de}^M$的维度转换为目标维度。

自相关机制

本文提出了一种序列级别联系的自相关机制，以提升信息利用。自相关通过计算序列的自相关性来发现时间段级别的依赖关系，并通过时间延迟聚合来合并相似的子序列。

时间段级别的依赖关系

不同时间段的相同位置的子过程通常是比较相似的，受随机过程理论启发，对于一个真实的离散时间过程 { X t } \{\mathcal X_t\} {Xt​}，可以通过如下公式计算出自相关关系。
$${\mathcal{R}}_{\mathcal{XX}}(\tau )=\underset{L\to \infty }{\lim }\frac{1}{L}\sum _{t=1}^L{\mathcal{X}}_t{\mathcal{X}}_{t-\tau }$$
${\mathcal{R}}_{\mathcal{XX}}(\tau )$反映了 { X t } \{\mathcal X_t\} {Xt​}和它落后$\tau$的序列 { X t − τ } \{\mathcal X_{t-\tau}\} {Xt−τ​}的时滞相似性。如上图Figure2所示，会取k个$\tau$，然后得到得到的$\mathcal{R}$就是一个置信度分数，这k个是根据置信度分数最高的k个选出来的。

时滞聚合

这个操作可以对齐相似的子序列，这些子序列位于估计时间段的相同相位位置，这与自注意力中的逐点点积聚合不同。最后，通过softmax归一化的置信度来聚合子序列。
τ 1 , ⋯   , τ k = arg ⁡ Topk ⁡ τ ∈ { 1 , ⋯   , L } ( R Q , K ( τ ) ) R ^ Q , K ( τ 1 ) , ⋯   , R ^ Q , K ( τ k ) = SoftMax ⁡ ( R Q , K ( τ 1 ) , ⋯   , R Q , K ( τ k ) )  Auto-Correlation  ( Q , K , V ) = ∑ i = 1 k Roll ⁡ ( V , τ i ) R ^ Q , K ( τ i ) , \begin{aligned} \tau_1, \cdots, \tau_k & =\underset{\tau \in\{1, \cdots, L\}}{\arg \operatorname{Topk}}\left(\mathcal{R}_{\mathcal{Q}, \mathcal{K}}(\tau)\right) \\ \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_1\right), \cdots, \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_k\right) & =\operatorname{SoftMax}\left(\mathcal{R}_{\mathcal{Q}, \mathcal{K}}\left(\tau_1\right), \cdots, \mathcal{R}_{\mathcal{Q}, \mathcal{K}}\left(\tau_k\right)\right) \\ \text { Auto-Correlation }(\mathcal{Q}, \mathcal{K}, \mathcal{V}) & =\sum_{i=1}^k \operatorname{Roll}\left(\mathcal{V}, \tau_i\right) \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_i\right), \end{aligned} τ1​,⋯,τk​R Q,K​(τ1​),⋯,R Q,K​(τk​) Auto-Correlation (Q,K,V)​=τ∈{1,⋯,L}argTopk​(RQ,K​(τ))=SoftMax(RQ,K​(τ1​),⋯,RQ,K​(τk​))=i=1∑k​Roll(V,τi​)R Q,K​(τi​),​
QKV就是将时间序列$\mathcal{X}$做映射后得到的，然后它就可以完全取代原来的self-attention

Topk是选出分数最高的几个自相关关系，$k=\lfloor c\times \log L\rfloor$，c是超参数，$\mathcal{R}$是自相关性，$Roll(\mathcal{X},\tau )$，就是将$\mathcal{X}$的前$\tau$长度的序列给移到最后的位置。

多头版本就是将隐藏层维度$d_{model}$给分成h份，${\mathcal{Q}}_i,{\mathcal{K}}_i,{\mathcal{V}}_i\in {\mathbb{R}}^{L\times \frac{d_{model}}{h}}$
$$\begin{array}{rl}\text{ MultiHead }(\mathcal{Q},\mathcal{K},\mathcal{V})& ={\mathcal{W}}_{\text{output }}\ast \text{ Concat }\left({\mathrm{head}}_1,\cdots ,{\mathrm{head}}_h\right)\\ \text{ where head }& =\text{ Auto-Correlation }\left({\mathcal{Q}}_i,{\mathcal{K}}_i,{\mathcal{V}}_i\right).\end{array}$$

更高效的计算

对于基于时间段的依赖关系，这些依赖关系指向底层时间序列的相同相位位置的子过程，并且本质上是稀疏的。

本文选取的是最有可能的几个时延，而且因为聚合的序列数是$\mathcal{O}(logL)$，所以整个计算复杂度是$\mathcal{O}(LlogL)$。

对于之前的自相关系数计算，可以采用基于Wiener-Khinchin快速傅里叶变换（FFT）来计算。
$$\begin{array}{rl}& {\mathcal{S}}_{\mathcal{XX}}(f)=\mathcal{F}\left({\mathcal{X}}_t\right){\mathcal{F}}^{\ast }\left({\mathcal{X}}_t\right)={\int }_{-\infty }^{\infty }{\mathcal{X}}_t{e}^{-i2\pi tf}\mathrm{d}t\overline{{\int }_{-\infty }^{\infty }{\mathcal{X}}_t{e}^{-i2\pi tf}\mathrm{d}t}\\ & {\mathcal{R}}_{\mathcal{XX}}(\tau )={\mathcal{F}}^{-1}\left({\mathcal{S}}_{\mathcal{XX}}(f)\right)={\int }_{-\infty }^{\infty }{\mathcal{S}}_{\mathcal{XX}}(f)e^{i2\pi f\tau }\mathrm{d}f\end{array}$$

自关联和自注意力的比较

不同于自注意力是数据点级别的关系构建，自关联是序列级别的，如下图所示：

相比于之前的点向连接的注意力机制或者其稀疏变体，自注意力（Auto-Correlation）机制实现了序列级的高效连接，从而可以更好的进行信息聚合，打破了信息利用瓶颈。

实验

数据集

1. ETT数据集是从电力变压器中收集的数据，包括负载和油温，记录了2016年7月至2018年7月之间每15分钟的数据。
2. Electricity1数据集包含了从2012年到2014年的321个客户的每小时电力消耗数据。
3. Exchange数据集记录了从1990年到2016年的八个不同国家的每日汇率数据。
4. Traffic2是来自加利福尼亚交通部的每小时数据，描述了旧金山湾区高速公路上不同传感器测量的道路占用率。
5. Weather3是记录了2020年全年的每10分钟天气数据，包括21个气象指标，如气温、湿度等。
6. ILI4包括了2002年至2021年美国疾病控制与预防中心记录的每周类似流感疾病（ILI）患者数据，描述了患有ILI的患者与总患者数量的比率。我们按照标准协议，按照6:2:2（ETT数据集）和7:1:2（其他数据集）的比例将所有数据集按时间顺序划分为训练集、验证集和测试集。

主要结果

多变量测试结果

对于所有benchmark和预测长度设置都达到sota，总的来说，在所有的实验中，Autoformer的平均MSE降低了38%。

此外，随着预测长度O的增加，Autoformer的性能变化相当稳定。这意味着Autoformer保持了更好的长期稳健性，这对于实际应用，如天气预警和长期能源消费规划等，具有重要意义。

单变量测试结果

Autoformer对于具有明显周期性的ETT数据集的input-96-predict-336设置，在均方误差（MSE）上实现了14%的降低。对于没有明显周期性的Exchange数据集，Autoformer在MSE上超过其他基准线17%，展现出更强的长期预测能力。此外，Autoformer在Exchange数据集的input-96-predict-96设置中，ARIMA模型表现最好，但在长期设置中失败。这种情况下，ARIMA模型可以从其对非平稳经济数据的固有处理能力中受益，但受到现实世界时间序列的复杂时间模式的限制。

消融实验

分解结构

本文提出的渐进分解结构运用到其它的模型也能够使模型效果获得提升，这说明该结构可以推广到其它模型，这个结构也优于预处理方法，因为它只关注了过去的数据，忽略了与未来的交互。

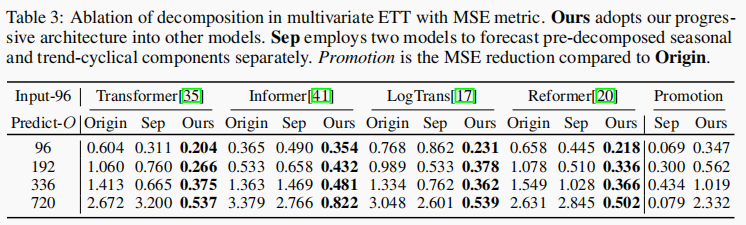
和self-attention变体的比较

本文也将auto-correlation换成self-attention及其变体进行了测试，发现auto-correlation依然能达到最好的表现。包括不同输入长度和输出长度的设置。

模型分析

时间序列分解

如果没有序列分解块，预测模型将无法捕捉季节性的增长趋势和峰值。并且随着分解块的增加，模型是能够实现渐进式的分解。

依赖学习

在最后一个时间步长中，自相关充分利用了所有相似的子序列，与自注意相比，没有遗漏或错误。这验证了Autoformer能够更充分、更准确地发现相关信息

复杂的季节性特征建模

Autoformer学到的滞后信息可以表示原始系列的真实季节性。每日记录的汇率数据集数据集呈现出月度、季度和年度周期(图6(b))。对于每小时记录的交通数据集(图6© ) ,学习到的滞后显示出24小时和168小时的间隔，与现实世界场景的日常和每周周期相匹配。这些结果表明，Autoformer可以从深层表示中捕捉到现实世界系列的复杂季节性，并提供可解释的人类预测。

效率分析

Autoformer在内存占用量和推理时间的表现都是非常优秀的，相较其它的self-attention方法有很大的提升。