因果推断之贝叶斯网络-C1（原理篇）

1. 贝叶斯定理解析（以疾病检测为例）

贝叶斯定理是概率论中的一个重要定理，描述了在给定某些观测证据的情况下，更新我们对某个事件发生概率的信念。

贝叶斯定理的数学公式如下：

其中：

• D：目标事件（患者是否患病）

• T：观测到的证据（检测结果为阳性）

• P(D)：先验概率，即在没有任何额外信息的情况下，某人患病的概率（如 0.1%）。

• P(T|D)：似然概率，即如果某人确实患病，检测为阳性的概率（如 90%）。

• P(T)：边际概率，即检测为阳性的总体概率，包括健康人和病人（综合所有情况的概率）。

• P(D|T)：后验概率，即在检测结果为阳性的情况下，患者实际患病的概率。

疾病检测案例

假设有一种罕见疾病，其在总体人群中的患病率为 0.1%（即 P(D) = 0.001）。现有一种检测方法：

• 对于真正的病人，检测为阳性的概率为 90%（即 P(T|D) = 0.9）。

• 对于健康的人，该检测方法也会产生 5% 的误检率（即 P(T|¬D) = 0.05）。

计算检测结果为阳性时，患者实际患病的概率：

我们使用全概率公式计算 P(T)（检测结果为阳性的总概率）：P(T)=P(T∣D)P(D)+P(T∣¬D)P(¬D)P(T)=P(T∣D)P(D)+P(T∣¬D)P(¬D)

代入数据：

然后，使用贝叶斯定理计算 P(D|T)（检测阳性时，患者患病的概率）：

即 1.77%，远低于 90%。

结论：虽然检测结果呈阳性，但真正患病的概率只有 1.77%，因为误检率较高，而疾病本身较罕见。

---

2. 贝叶斯网络基本结构

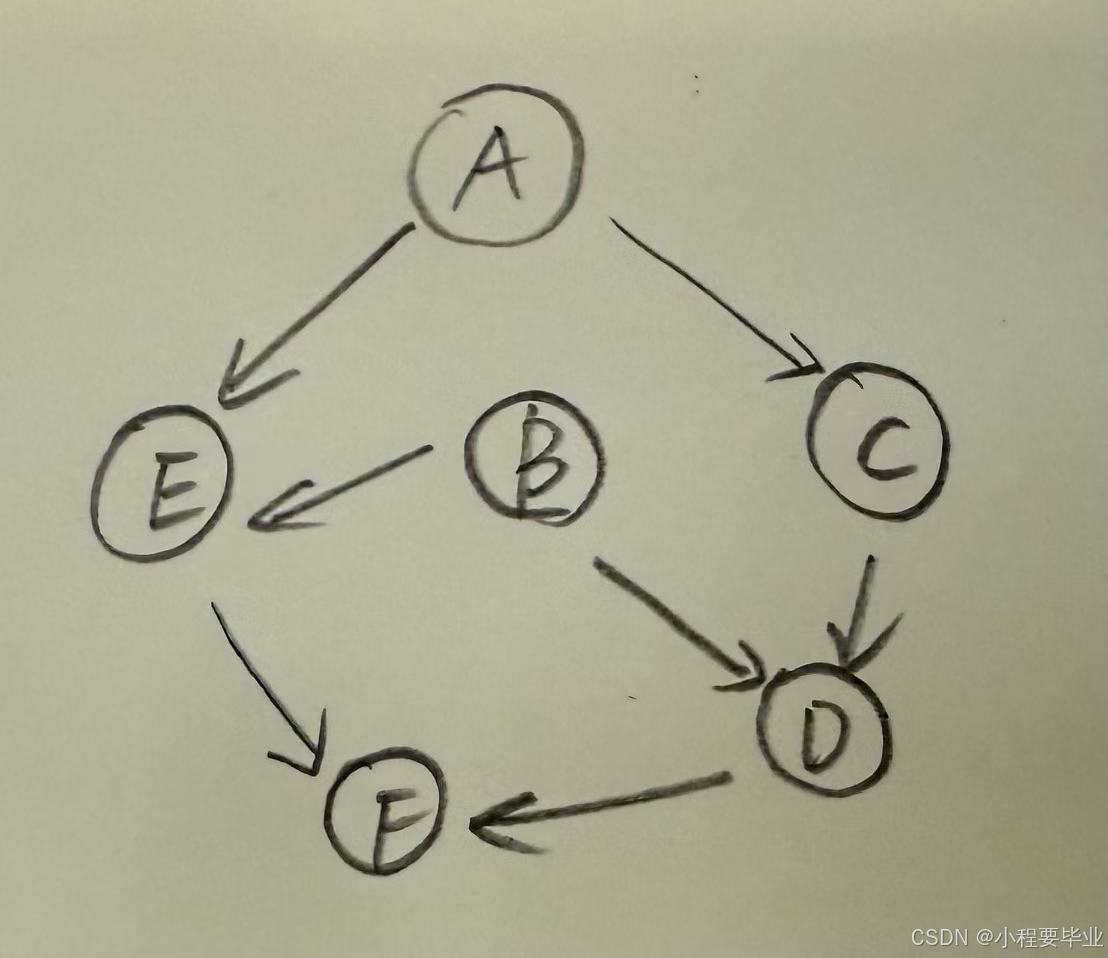
贝叶斯网络是一种概率图模型，用于表示变量之间的条件独立性关系。它使用有向无环图（DAG），其中：

• 节点（Nodes）：表示随机变量。

• 有向边（Edges）：表示因果关系或条件依赖。

• 联合概率：可分解为各节点的条件概率乘积。

联合概率公式

对于一个贝叶斯网络，我们可以用如下公式表示联合概率分布：

这种分解方式减少了计算复杂度，使得概率计算更加高效。

---

3. 贝叶斯网络的三种基本结构

(1) 链式结构（Chain）

示例：

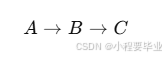
• A：考大学 → B：上大学 → C：获得更好工作

• 条件独立性：已知 B 的情况下，A 和 C 独立，即：

• 

(2) 分叉结构（Fork）

示例：

• A：擅长数学

• B：数学成绩好

• C：物理成绩好

条件独立性：已知 B 后，A 和 C 条件独立，即：

(3) 汇聚结构（Collider）

示例：

• A：去华为面试

• B：是否被录取

• C：竞争者的表现

条件独立性：A 和 C 本来是独立的，但如果知道了 B，则 A 和 C 变得相关。

• 未知 B 时：

• 

• 已知 B 时：

• 

注：大家有不明白的可以去听这个up主的讲解，很清晰！感谢up主分享！👉【【因果推断②】贝叶斯网络 | 为什么？|暑假】https://www.bilibili.com/video/BV1n14y1t7wR?vd_source=32205851661d6d64c03532c63993928c