最小二乘法的几何解释

最小二乘法的几何解释

这篇文章用通俗易懂的语言，从几何的角度解释了最小二乘法的解为什么是$\hat{x}={{\left( {{A}^{T}}A \right)}^{-1}}{{A}^{T}}b$

线性方程组的几何意义

---

为了从几何的角度解释最小二乘法，我们先回顾一下，线性方程组的几何意义。线性方程组可以从行和列两个角度看。
举例，看如下简单的线性方程组：

$$\left\{ \begin{array}{l} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {x_1} + {x_2} = 3{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \leftarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} a\\ - {x_1} + {x_2} = 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \leftarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} b{\mkern 1mu} \end{array} \right.$$

从行的角度看

线性方程组的解就是直线$a$和直线$b$的交点，这一点应该谁都知道，如下图所示：

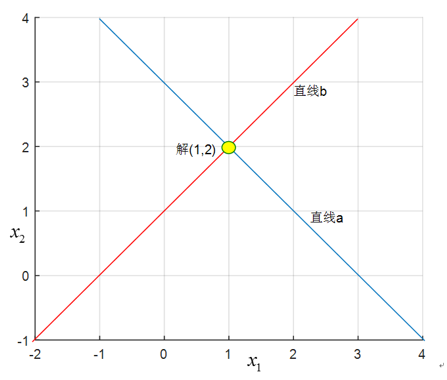
从图上很容易可以看出该线性方程组的解为 $x_1=1,x_2=2$,

所以从行的角度看，线性方程组的每一行都代表空间中的几何图形（二维时是直线，三维时是平面，高维时是高维空间中的一个”平面“），线性方程组的解就是这些图形的交点or交线or交面。

从列的角度看

从列的角度看时，先把上面的线性方程组写成矩阵的形式

$$\begin{array}{l} \left[ \begin{array}{l} {\rm{ \ \ 1 \ \ \ 1}}\\ {\rm{ - 1 \ \ 1}} \end{array} \right] \times \left[ \begin{array}{l} {x_1}\\ {x_2} \end{array} \right] = \left[ \begin{array}{l} 3\\ 1 \end{array} \right]\,\\ \,\,\,\,\, \uparrow \,\,\,\,\,\,\, \uparrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \uparrow \\ \,\,\,\,\,{a_1}\,\,\,\,\,{a_2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b \end{array}$$
这样看还不是很直观，再把上式拆开，写成下面这个样子：

[1−1]×x1+[11]×x2=[31