【三维数域】超详细步骤！空间数据索引的创建算法全过程！

在处理二三维空间数据时，为提高检索效率，时常需要创建二、三维空间数据索引，区别在于三维索引创建需要考虑额外的维度（通常是空间中的x, y, z坐标）。

在处理二、三维数据时，常用的索引结构包括R树、K-D树、四叉树和八叉树等。本文将详细介绍如何选择空间索引和数据索引的创建算法步骤。

一、常见空间数据索引概览

• R树：广泛用于空间数据索引，适用于包含不规则形状的空间数据。R树通过将空间划分成矩形区域来存储数据。
• K-D树：通过递归划分空间，使用轴对齐的平面将空间划分为多个子空间。K-D树适用于范围查询和最近邻查询。

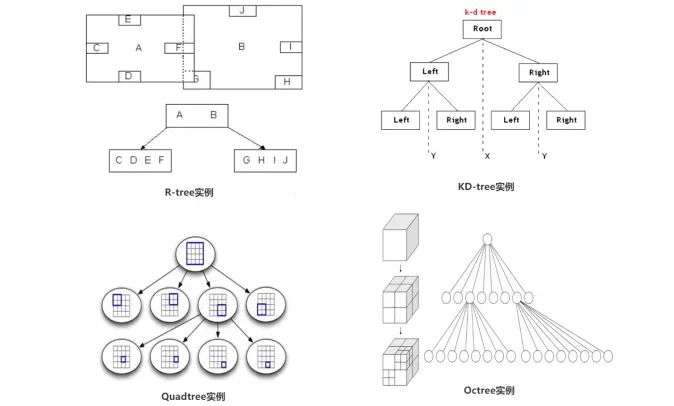
索引概览 图源：Mapmost Studio

四叉树：四叉树是二维空间的八叉树的对应形式，用于二维空间划分。在三维空间中，四叉树可以看作是每个节点分为四个相等的矩形区域。四叉树常用于图像处理和地形分析。

• 八叉树：是一种基于立方体的分层索引结构，通常用于3D点云数据、体素数据等。八叉树的每个节点表示一个正方体的体积元素，每个节点有八个子节点，这八个子节点所表示的体积元素加在一起就等于父节点的体积。一般中心点作为节点的分叉中心。八叉树若不为空树的话，树中任一节点的子节点恰好只会有八个，或零个，也就是子节点不会有0与8以外的数目。

二、空间数据索引创建步骤

空间数据索引创建通常根据不同空间数据类型和适应场景经过数据索引设计、索引数据结构选择、索引构建、索引优化四个步骤。以下是详细实现过程。

#数据索引设计

空间数据索引设计是性能优化的关键部分，它能够显著提高查询效率、减少响应时间，并改善整体系统性能。良好的索引设计不仅能加速读取操作，还能通过减少锁争用和优化写入路径来间接提升写入性能。不同数据类型常需要设计不同的数据索引类型。在设计索引时要确定数据的特点，根据数据类型（几何空间数据、三维模型、点云数据等）选择合适的索引结构。需要考虑的因素包括：

• 数据的分布：均匀分布的点适合使用K-D树和四叉树，而不规则分布的空间数据更适合使用R树。
• 数据密度：如果数据在某些区域特别密集，则应选择能够处理高密度数据的索引结构（如 R树），并可能需要调整索引参数或使用自适应分区。
• 查询类型：如果查询是范围查询或邻域查询，可以选择K-D树；如果是包含复杂形状的多维数据，R树可能更合适。
• 实时性要求：如果系统对实时响应有较高要求，应避免过于复杂的索引结构，以免增加写入延迟。

#数据结构选择

下表记录了R树、K-D树、四叉树和八叉树适用数据、应用场景、优势和劣势情况，可根据空间数据特点选择不同的索引类型。

空间索引类型表 表源：Mapmost Studio

#数据索引构建

R树构建步骤

构建 R树 是一个递归的过程，旨在将空间对象组织成层次化的矩形包围盒（MBR, Minimum Bounding Rectangle），从而加速查询操作。以下是构建 R树 的详细步骤：

初始化

• 定义根节点，创建一个空的根节点，该节点将是树的起点。
• 设置插入策略，选择合适的插入策略，如 Guttman's Quadratic Split 或 R*树 的优化插入方法。

构建最小外接矩形（MBR）

• 为每个空间对象计算其最小外接矩形（MBR）。对于点数据，MBR 就是该点本身；对于复杂几何形状，则是能够完全包含该形状的最小矩形。 

插入操作

• 选择插入位置：
  递归查找合适叶子节点，从根节点开始，递归地选择最合适的叶子节点来插入新对象。选择标准通常是使新增加的对象导致 MBR 扩展最少的节点。对于内部节点，选择扩展增量最小的子节点。如果有多个子节点扩展增量相同，则选择当前 MBR 面积最小的子节点。
• 处理叶子节点溢出：
  检查节点容量，如果选定的叶子节点未满（即未达到预设的最大条目数），则直接将新对象插入该节点，并更新其 MBR。处理溢出，如果叶子节点已满，则需要进行分裂操作。
• 节点分裂：
  选择分裂策略，常见的分裂策略包括线性分裂、二次分裂（Quadratic Split）或优化的分裂算法（如 R*树 中使用的策略）。创建新节点，根据分裂结果创建两个新的节点，并将原节点的对象重新分配到这两个新节点中。更新父节点，将新创建的两个节点作为子节点添加到父节点，并更新父节点的 MBR。如果父节点也溢出，则继续向上层传播分裂操作，直到找到可以容纳新子节点的节点或创建新的根节点。

调整优化

• 在插入过程中尽量减少节点之间的重叠，以提高查询效率。通过适当的插入策略和分裂算法保持树的高度较低且平衡，避免出现过度倾斜的情况。

K-D树构建步骤

K-D树构建伪代码：

输入: 大量无序化的点云，维度3
输出：点云对应的kd-tree数据结构
构建过程：
1、初始化分割轴：对每个维度的数据进行方差的计算，取最大方差的维度作为分割轴；
2、确定节点：对当前数据按分割轴维度进行检索，找到中位数数据，并将其放入到当前节点上；
3、划分双支：
    划分左支：在当前分割轴维度，所有小于中位数的值划分到左支中；
    划分右支：在当前分割轴维度，所有大于等于中位数的值划分到右支中。
4、更新分割轴：继续选择方差最大的轴作为分割轴（或者随机选择、或顺序选择）;
5、确定子节点：
    确定左节点：在左支的数据中进行步骤2；
    确定右节点：在右支的数据中进行步骤2；

四叉树构建步骤

四叉树构建可参照下述代码实现，下述代码实现了一个简单的四叉树数据结构，用于高效管理二维空间中的点。它包含以下功能：

• 点的表示：Point 类用于定义点的坐标。
• 节点管理：QuadtreeNode 类表示四叉树的节点，负责存储点、判断点是否在边界内，以及分裂节点。
• 插入逻辑：insert 方法将点插入到节点中，当节点超出容量时会自动分裂成四个子节点，并将点分配到对应的子节点中。
• 递归分裂：subdivide 方法将当前节点细分为四个象限，分别管理各区域的点。

运行示例中，程序创建了一个边界为 (0, 0, 100, 100) 的四叉树，并插入若干点，最终输出四叉树的结构。Python构建四叉树示例：

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def __repr__(self):
        return f"Point({self.x}, {self.y})"
class QuadtreeNode:
    def __init__(self, boundary, capacity):
        self.boundary = boundary  # 边界是一个元组：(x_min, y_min, x_max, y_max)
        self.capacity = capacity  # 当前节点的最大容量
        self.points = []          # 当前节点包含的点
        self.divided = False      # 节点是否已被细分
        self.children = []        # 子节点列表：[NW, NE, SW, SE]
    def insert(self, point):
        # 检查点是否在边界内
        if not self._in_boundary(point):
            return False
        # 如果节点有空间，直接添加点
        if len(self.points) < self.capacity:
            self.points.append(point)
            return True
        # 否则，细分节点并将点分配给子节点
        if not self.divided:
            self.subdivide()
        for child in self.children:
            if child.insert(point):
                return True
        return False
    def _in_boundary(self, point):
        x_min, y_min, x_max, y_max = self.boundary
        return x_min <= point.x < x_max and y_min <= point.y < y_max
    def subdivide(self):
        x_min, y_min, x_max, y_max = self.boundary
        mid_x = (x_min + x_max) / 2
        mid_y = (y_min + y_max) / 2
        self.children = [
            QuadtreeNode((x_min, y_min, mid_x, mid_y), self.capacity),  # 左上 (NW)
            QuadtreeNode((mid_x, y_min, x_max, mid_y), self.capacity),  # 右上 (NE)
            QuadtreeNode((x_min, mid_y, mid_x, y_max), self.capacity),  # 左下 (SW)
            QuadtreeNode((mid_x, mid_y, x_max, y_max), self.capacity)   # 右下 (SE)
        ]
        self.divided = True
    def __repr__(self):
        return f"QuadtreeNode(boundary={self.boundary}, points={self.points}, divided={self.divided})"
# 示例使用
boundary = (0, 0, 100, 100)  # 定义四叉树的边界
quadtree = QuadtreeNode(boundary, capacity=4)  # 创建一个容量为4的四叉树
points = [Point(10, 10), Point(20, 20), Point(30, 30), Point(40, 40), Point(50, 50)]
for point in points:
    quadtree.insert(point)
print(quadtree)
#QuadtreeNode(boundary=(0, 0, 100, 100), points=[Point(10, 10), Point(20, 20), Point(30, 30), Point(40, 40)], divided=True)

八叉树构建步骤

八叉树是一种用于三维空间的数据结构，它通过递归地将空间划分为更小的立方体来组织数据。以下是构建八叉树的基本步骤：

步骤一：

设定最大递归深度 max_depth。

步骤二：

找出场景的最大尺寸，并以此尺寸建立第一个立方体。

步骤三：

依序将单位元元素丢入能被包含且没有子节点的立方体。

步骤四：

若没达到最大递归深度，就再次进行细分八等份，再将该立方体所装的单位元元素全部分担给八个子立方体。

步骤五：

若发现子立方体所分配到的单位元元素数量不为零且跟父立方体是一样的，则该子立方体停止细分，因为根据空间分割理论，细分的空间所得到的分配必定较少，若是一样数目，则再怎么切数目还是一样，会造成无穷切割的情形。

步骤六：

重复步骤三，直到达到最大递归深度。

八叉树细分示意图 图源：Mapmost Studio

#数据索引优化

三维索引在实际应用中常用于点云处理、三维模型检索、地理信息系统等领域。优化方法包括：

• ‌平衡因子控制‌：确保树的深度大致相同，避免不平衡导致的性能下降。
• ‌动态调整‌：根据数据变化动态调整树的结构，保持高效性。
• ‌并行处理‌：利用多核处理器并行处理数据插入、查询等操作，提高效率。

空间数据索引的创建需要考虑数据的特点、查询的类型以及索引结构的选择。R树、K-D树、四叉树和八叉树是常用的数据索引结构，每种结构在不同应用场景下有不同的优势。在实际应用中，合理选择索引结构并进行优化，能够显著提高三维数据的查询效率。

Mapmost Studio中用到了多种空间索引方式，矢量地图服务发布使用了R树，三维模型服务发布使用了八叉树，对影像、地形等服务发布使用了四叉树索引，大大提升了加载性能，为用户提供更优质的产品体验，助你通过简单几步操作即可尽享空间索引所带来的性能提升。

产品现已开放在线体验版，点击此处前往Mapmost官网体验！