线性代数：空间的基

1、空间的基的概念

若$m$个向量生成$n$维${\vec{v}}_1,{\vec{v}}_2,{\vec{v}}_3,\cdots ,{\vec{v}}_m$空间，$m$最小是为$n$；
若$m>n$，则${\vec{v}}_1,{\vec{v}}_2,{\vec{v}}_3,\cdots ,{\vec{v}}_m$线性相关；
若$m$个$n$维向量线性无关，$m$最大为$n$。
$理解线性无关:$
$求证线性无关等价于求证是否存在一组全为的系数k,使得k_1\cdot {\vec{v}}_1+k_2\cdot {\vec{v}}_2+k_3\cdot {\vec{v}}_3+\cdots +k_m\cdot {\vec{v}}_m=0\iff 转而判断m个n维向量组成的系数矩阵A\cdot \vec{k}=0有唯一零解$
$m个不共线的n维向量组成的线性系统A\cdot \vec{k}=0，是一个方程数大于未知数的线性系统，且行阶梯式的非零行个数等于未知数个数，所以有唯一零解，证得m个(m<n)个n维向量线性无关$

若一组向量可以生成整个$n$维空间，且线性无关，这组向量一定有$n$个，则称这组向量为这个$n$维空间的一组$基(bases)$

因为可以生成整个$n$维空间的$n$个线性无关的$n$维向量可以有无数组，所以一个空间可以有无数组基。

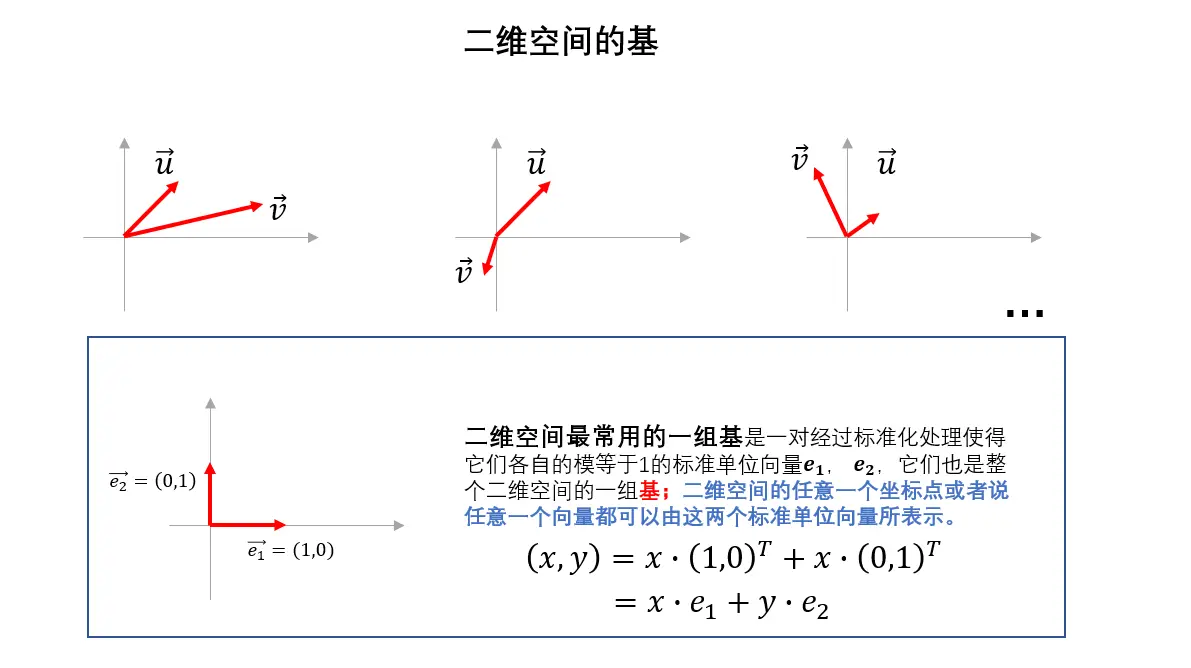
从一个低维空间–二维空间来看待空间的基

在二维空间中，任取两个不共线的向量$\vec{u}$和$\vec{v}$，它们就是二维空间的一组基，任意第三个向量都可以表示为$\vec{u}$和$\vec{v}$的线性组合。

基可以理解为一个初等数学接触的坐标系概念，${\vec{e}}_1，{\vec{e}}_2$是二维空间一组坐标系，$\vec{u}，\vec{v}$也是一组坐标系，在这些坐标系下都可以观测到二维空间的任意一个点，区别在于不同的坐标系空间中同一个点的表示方式是不一样的。

给定$n$维空间的一组基，则空间中的任意一个向量都可以表示成这组基的线性组合，且这个向量在这组基下的表示方法唯一。

证明：对$n$维空间中的任意一个向量$\vec{u}$，求证是否一定存在一组$k$，使得：
$k_1\cdot {\vec{e}}_1+k_2\cdot {\vec{e}}_2+\cdots +k_n\cdot {\vec{e}}_n=\vec{u}$
等价于求解线性系统:$\left[\begin{array}{ccc}1& 0& \cdots 0\\ 0& 1& \cdots 0\\ \cdots & \cdots & \cdots \\ 0& 0& \cdots 1\end{array}\right]\left[\begin{array}{c}{k}_1\\ k_2\\ \cdots \\ k_n\end{array}\right]=\left[\begin{array}{c}{u}_1\\ u_2\\ \cdots \\ u_n\end{array}\right]$
对于这个线性系统，系数矩阵$A$一定可逆，所以一定有解，且有唯一解$(A\cdot x=b\to x=A^{-1}\cdot b)$

2、空间的基的性质

• n维空间中，任意n个线性无关的向量，一定是这个n维空间的基；
• n维空间中，额如果n个向量可以生成整个空间，则这n个向量，是这个n维空间的基；
• 如果一组向量${\vec{v}}_1,{\vec{v}}_2,\cdots ,{\vec{v}}_p$可以生成$n$维空间$(p\ge n)$，则这组向量的存在一个子集，是$n$维空间的一组基。— 该结论表明，很多时候，我们并不需要构造$n$维空间的一组基如果，当存在$p$个向量可以生成整个$n$维空间的时候，只需要从这组向量里挑选出一个包含$n$个线性无关向量的子集就可以成为这个$n$维空间的一组基

对于$m$个线性无关的$n$维向量，若$m<n$，这$m$个向量无法生成整个空间；降低到三维空间来理解就是，如果只给出两个三维空间的向量$\vec{u},\vec{v}$，它们只能形成一个平面，则这两个向量的任意线性组合都在平面上，无法生成不在平面的向量。当$m=n$ 时，$m$个线性无关的$n$维向量可以生成整个空间，且可以成为空间的基。当$m>n$，此时这$m$个向量变成线性相关组，可以生成整个空间但不是空间的基。