Random Features for Large-Scale Kernel Machines阅读

       本文Random Features for Large-Scale Kernel Machines提出两种 randomized feature maps 来近似平移不变核 。
$文中符号{}^{\prime }表示转置$

方法一	方法二
试图从核函数的傅里叶变换中随机抽取正弦来组成	以随机选择的分辨率使用随机移动的网格划分输入空间
映射是平滑的	映射非平滑的
适合插值任务	适合于近似依赖于数据点之间的L1距离的内核
采样自$p(\omega )$

随机傅里叶特征

         随机特征，由随机傅里叶变换基$$cos(w^{\prime }x+b),其中w\in R^d,b\in R是随机变量$$

其将数据点投影到随机选择的线上，然后使用正弦函数传递标量结果 (see Figure 1 and Algorithm 1)。从适当的分布中选取这些线的方向可以保证两个变换点的乘积将近似于所需的移位不变核。

Theorem 1 (Bochner [13])¹

$R^d上的一个连续的核k(x,y)=k(x-y)如果是正定的$²$当且仅当k(\delta )是一个非负测度的傅里叶变换。$$如果平移不变核k(\delta )被相应地缩放，Bochner定理保证了它的Fourier变换p(\omega )是一个相应的概率分布。$

$令{\zeta }_{\omega }(x)=e^{j{\omega }^{\prime }x}$
$$k(x-y)={\int }_{R^d}p(\omega )e^{j{\omega }^{\prime }(x-y)}d\omega =E_w[{\zeta }_{\omega }(x){\zeta }_{\omega }(y{)}^{\ast }]$$
$所以当w\sim p，{\zeta }_{\omega }(x){\zeta }_{\omega }(y{)}^{\ast }是k(x,y)的无偏估计$

由于概率分布p（ω）和核k(∆) 都是实的，当复指数替换为余弦时，积分（2）收敛。因此，我们可以令 $z_{\omega }(x)=\sqrt{2}cos({\omega }^{\prime }x+b)$,以得到满足条件$E[z_{\omega }(x)z_{\omega }(y)]=k(x,y)$的实值映射。$其中\omega 取自分布p(\omega ),b取自[0,2\pi ]上的均匀分布。$$z_{\omega }(x)z_{\omega }(y)的期望值k(x,y)可由角度公式求和得出。$

我们可以通过将随机选择的D个zω连接到一个D维向量z中，并用√D对每个分量进行归一化来降低核估计的方差。内积$z(x{)}^{\prime }z(y)={\sum }_{j=1}^D{z}_{w_j}(x)z_{w_j}(y)是z_{\omega }的样本平均值$，因此是期望值（2）的较低方差近似值。
因为对于特定的x和y，$z_{\omega }的边界在-\sqrt{2}和+\sqrt{2}之间$，Hodeffding不等式保证了z(x)'z(y)和k(x,y)之间在D中的指数快速收敛：
$$Pr[|z(x)0z(y)-k(x,y)|\ge ϵ]\le 2exp(-D{ϵ}^2/4)$$

基于这一观察，可以对输入空间中的每一对点同时证明一个更有力的断言：
Claim 1:（傅里叶特征的一致收敛性）
$设M是直径为diam(M)的R^d中的紧子集。然后，对于映射z，我们有$

$$其中{\sigma }_p^2(E_p({\omega }^{\prime }\omega ))是k的傅里叶变换的二阶矩。$$
这个断言的证明详见附录。
根据标准的傅里叶恒等式，标量${\sigma }_p^2$等于k海森矩阵的迹在0处的值。它量化了核在原点处的曲率。
$ForthesphericalGaussiankernel,k(x,y)=exp(-\gamma ||x-y|{|}^2),wehave{\sigma }_p^2=2d\gamma .$

一点扩展：
对于非平移不变的kernel，可以通过平移不变的逐渐近似；
对于随机采样，可以通过QMC和正交采样等方式降低随机性和计算复杂度。

Random Binning Features 随机装箱特征

       以随机选择的分辨率且使用随机移动的网格划分输入空间，重复这个操作P次，并为输入点分配一个二进制位字符串，该字符串对应于其所在的存储单元（参见图2和算法2）。
因为它使用直线网格，这种映射非常适合只依赖于点对之间的L1距离的核。网格的构造使得两个点x和y被分配到同一个箱子的概率与k(x，y)成正比。一对变换点之间的内积与两个点组合在一起的次数成正比，因此是k(x，y)的无偏估计。

(左)该算法以随机选择的分辨率和使用随机移动的网格重复划分输入空间，然后得到每个点x的与分配给它的箱子关联的bit串z(x)。（右）描述这种划分的二元邻接矩阵的第ij个条目中的$z(x_i{)}^{\prime }z(x_j)$，此方法是核矩阵的无偏估计。

原因

Kernel machines：
给 定 { x n , y n } n = 1 N , 在 不 考 虑 偏 置 的 情 况 下 f = W T x 但 是 我 们 思 考 以 下 ( 图 一 ： 深 蓝 色 ， 浅 蓝 色 ) 的 二 分 类 问 题 ： 左 侧 为 逻 辑 回 归 ， 右 侧 为 核 方 法 中 著 名 的 非 线 性 支 持 向 量 机 给定\{x_n,y_n\}_{n=1}^N,在不考虑偏置的情况下\\ f=W^Tx\\ 但是我们思考以下(图一：深蓝色，浅蓝色)的二分类问题：\\ 左侧为逻辑回归，右侧为核方法中著名的非线性支持向量机 给定{xn​,yn​}n=1N​,在不考虑偏置的情况下f=WTx但是我们思考以下(图一：深蓝色，浅蓝色)的二分类问题：左侧为逻辑回归，右侧为核方法中著名的非线性支持向量机

        Mercer’s theorem表明可以存在一个特征映射$\phi :X\to V$
$$k(x,y)=<\phi (x),\phi (y)>v$$

$$\begin{gathered} 使用核方法可以使用线性的方法构建一个非线性模型： \\ f=\sum _{n=1}^N{a}_{n}k(x,x_n)=<w,\phi (x)>v \end{gathered}$$

但是许多和方法需要计算和操作N×N的协方差矩阵。在大数据领域，内核方法不一定可以扩展。

在原因部分提到了计算机难以支持核方法对大规模数据协方差矩阵的计算。由此引出Random features。构造一个“随机”映射Z使得：

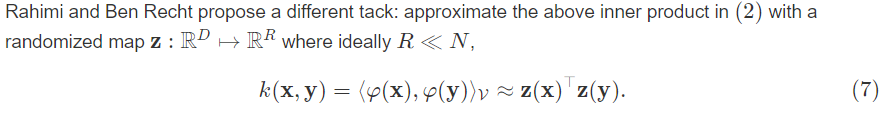
即用z将数据映射到高维空间代替核函数隐性的映射到高维。

video : the theoretical guarantees of this approximatio
http://www.argmin.net/2017/12/05/kitchen-sinks/
机器学习有很多关于核函数的说法，核函数的定义和作用是什么？

---

参考：
https://gregorygundersen.com/blog/2019/12/23/random-fourier-features/
https://gregorygundersen.com/blog/2019/12/10/kernel-trick/
random feature map的SVM是不是和extreme learning machine很像
Random Features for Large-Scale Kernel Machines (Rahimi & Recht, 2007)
NIPS 网站 ：https://neurips.cc/
NIPS 2017首日亮点全解读：四大获奖论文结果揭晓
获奖论文列表

什么是 bochner 技巧？
随机傅里叶特征(Random Fourier Features)
随机傅里叶特征(Random Fourier Features)
随机装箱算法（Random Binning Features）
添加链接描述

代码：

import numpy as np
import pandas as pd
df = pd.read_csv('adult_onehot.csv')
X = df.iloc[:200,:].values
def k(x,y):
    return np.exp(-np.linalg.norm(x-y)**2)
rows = []
for i in range(X.shape[0]):
    row=[]
    for j in range(X.shape[0]):
        row.append(k(X[i],X[j]))
    rows.append(np.hstack(row))    
K = np.vstack(rows)

D = 1000
W = np.random.randn(D,X.shape[1])
b = np.random.rand(D)

def z(x):
    return np.cos(W@x+b)
    
def zxzy(x,y):
    return 2.0/D*z(x).T@z(y)
rows = []
for i in range(X.shape[0]):
    row=[]
    for j in range(X.shape[0]):
        row.append(zxzy(X[i],X[j]))
    rows.append(np.hstack(row))    
Z = np.vstack(rows) # 按行顺序堆叠数组构成一个新的数组，dim=0

随机装箱算法相关论文
网站的幻灯片

https://github.com/qw3rtman/random-feature-maps

这里直接引用了以上链接的代码：

"""Random Fourier Feature"""

import numpy as np
from syllabus import Task

from .raw_array import make_raw
from .sample import KERNELS, sample, sample_1d


class RandomFourierFeature:
    """Random Fourier Feature
    Parameters
    ----------
    d : int
        Input space dimension
    D : int
        Feature space dimension
    W : RawArray or None
        If not None, used as the transformation matrix W instead of
        generating a new matrix
    b : RawArray or None
        If not None, used as the offset coefficients b
    kernel : char
        Kernel to use; 'G', 'L', or 'C'
    References
    ----------
    ..  [1] A. Rahimi, B. Recht, "Random Features for Large-Scale Kernel
        Machines"
    """

    def __init__(self, d, D, W=None, b=None, kernel='G', task=None):

        self.d = d
        self.D = D

        kernel = kernel.upper()
        if kernel not in ['G', 'L', 'C']:
            raise Exception('Invalid Kernel')
        self.kernel = kernel

        if W is None or b is None:
            self.__new(task)
        else:
            self.__load(W, b)

    def __load(self, W, b):
        """Load from existing RawArrays"""

        self.W = np.frombuffer(W, dtype=np.float32).reshape([self.D, self.d])
        self.b = np.frombuffer(b, dtype=np.float32)

    def __new(self, task):
        """Create new W and b"""

        if task is None:
            task = Task()
        task.start(name='Random Fourier Feature', desc=self.__str__())

        # Create feature
        self.create()

        task.done(
            self.W, self.b, desc="{desc} created".format(desc=self.__str__()))

    def mp_package(self):
        """Package into a multiprocessing-ready RawArray
        Returns
        -------
        (int, int, np.array, np.array)
            [0] input dimension (d)
            [1] output dimension (D)
            [2] W matrix (shape=(D, d))
            [3] b matrix (shape=(D))
        """

        if not hasattr(self, 'W_raw') or not hasattr(self, 'b_raw'):
            self.W_raw = make_raw(self.W)
            self.b_raw = make_raw(self.b)

        return (self.d, self.D, self.W_raw, self.b_raw)

    def create(self):
        """Create a d->D fourier random feature"""

        self.b = np.random.uniform(0, 2 * np.pi, self.D)

        if self.kernel == 'G':
            random_vectors = [
                np.random.normal(0, 1, self.d) for _ in range(self.D)]
            self.W = np.array([
                vector *
                (
                    sample_1d(KERNELS[self.kernel], [-10, 10]) /
                    np.linalg.norm(vector)
                )
                for vector in random_vectors
            ], dtype=np.float32)
        else:
            self.W = np.reshape(
                np.array([
                    sample(KERNELS[self.kernel], self.d)
                    for _ in range(self.D)], dtype=np.float32),
                (self.D, self.d))

    def transform(self, x):
        """Transform a vector using this feature
        Parameters
        ----------
        x : np.array (shape=(d))
            Array to transform; must be single dimension vector
        Returns
        -------
        x : np.array (shape=(D))
            Feature space transformation of x
        """
        return np.sqrt(2 / self.D) * np.cos(np.dot(self.W, x) + self.b)

    def __str__(self):
        """Get string representation
        Shown as "<d>-><D> Random Fourier Feature"
        """
        return (
            "{d}->{D} Random Fourier Feature"
            .format(d=self.d, D=self.D))

"""Random Binning Feature"""

import numpy as np
import math
from syllabus import Task
from .sample import sample, ft_laplacian
from .raw_array import make_raw


def get_p_set(args):
    """Generate one set of deltas (bin width) and mus (bin offset)
    Parameters
    ----------
    n : int
        Number of dimensions
    task : Task
        task parent
    Returns
    -------
    (np.array, np.array)
        [0] delta vector for this feature
        [1] mu vector for this feature
    """

    n, task = args

    delta_p = sample(ft_laplacian, n)
    mu_p = [np.random.uniform(0, delta_m) for delta_m in delta_p]

    if task is not None:
        task.done(silent=True)
    return (delta_p, mu_p)


class RandomBinningFeature:
    """Random Binning Feature
    Parameters
    ----------
    d : int
        Input space dimension
    D : int
        Feature space dimension; actual dimension is 128 * D binary array
    cores : int
        Number of cores to use for generation
    task : Task or none
        Task to register feature generation under
    """

    def __init__(self, d, D, delta=None, mu=None, cores=None, task=None):

        self.d = d
        self.D = D

        if delta is None or mu is None:
            self.__new(task, cores)
        else:
            self.__load(delta, mu)

    def __load(self, delta, mu):
        self.delta = np.frombuffer(
            delta, dtype=np.float32).reshape([self.D, self.d])
        self.mu = np.frombuffer(
            mu, dtype=np.float32).reshape([self.D, self.d])

    def __new(self, task, cores):

        if task is None:
            task = Task()
        task.start(name='Random Binning Feature', desc=self.__str__())

        gen = task.pool(
            get_p_set, [self.d for _ in range(self.D)],
            cores=cores, process=True, name='Random Binning Feature')

        self.delta = np.array([x[0] for x in gen], dtype=np.float32)
        self.mu = np.array([x[1] for x in gen], dtype=np.float32)

        task.done(
            self.delta, self.mu,
            desc="{desc} created".format(desc=self.__str__()))

    def mp_package(self):

        if not hasattr(self, 'delta_raw') or not hasattr(self, 'mu_raw'):
            self.delta_raw = make_raw(self.delta)
            self.mu_raw = make_raw(self.delta)

        return (self.d, self.D, self.delta_raw, self.mu_raw)

    def transform(self, x):
        """Transform a vector using this feature
        Parameters
        ----------
        x : np.array (shape=(d))
            Array to transform; must be a single dimension vector
        Returns
        -------
        x : np.array (shape=(D))
            Feature space transformation of x
        """
        ret = []
        for mu_p, delta_p in zip(self.mu, self.delta):
            tmp = [0 for i in range(128)]
            for x_i, mu, delta in zip(x, mu_p, delta_p):
                tmp[math.ceil((x_i - mu) / delta) % 128] += 1
            ret += tmp

        return 1 / np.sqrt(self.D) * np.array(ret, dtype=np.uint8)

    def __str__(self):
        """Get String representation
        Shown as "<d>-><D> Random Binning Feature"
        """
        return (
            "{d}->{D} Random Binning Feature"
            .format(d=self.d, D=self.D))

---

1. 调和分析的经典定理。可参见W. Rudin. Fourier Analysis on Groups. Wiley Classics Library. Wiley-Interscience, New York, reprint edition edition, 1994. wiki ↩︎

2. https://math.stackexchange.com/questions/2754657/conditions-for-a-nonnegative-fourier-transform
   https://en.wikipedia.org/wiki/Positive-definite_function_on_a_group ↩︎