企业实际业务中,总有一些费用难以明确指定属于哪个成本中心,比如公共费用、行政费用,在SAP里的处理方法就是将其归纳到公共成本中心中,然后按照一定的规则分配 分摊到其他成本中心。
例如,企业内有有几个生产车间,在生成过程中产生了水电费,在收到发票后,先将费用归集到公共的成本中心,然后根据各个车间的耗电量或者产量进行分摊,在CO模块里,首先定义分摊规则,一般是根据产量或者固定比例进行分摊分配。
分配是将费用以初级成本要素从发送方转给接收方,分摊是将费用以次级成本要素的形式从发送方转到接收方,例如某个公司公共成本中心收集到的水电费如下,分配规则是按照固定比例;

如果以分配的方式将水电费用分给三个生产车间,分配完成后,费用是以初级成本要素的形式流入三个生产车间;

如果是以分摊的形式将水电费分给三个生产车间,分摊结束后,公共成本中心的余额应该是0,通过次级成本要素 制造费用 流向三个生产车间;
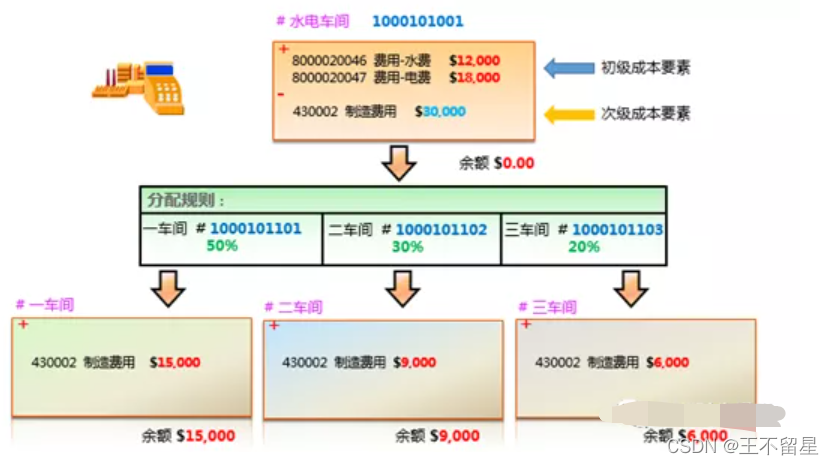
两者的区别主要在于分摊是将费用统一进次级成本要素之后进行拆分进入生产成本中心,分配是以初级成本要素的方式直接进入三个成本中心,一个次级成本要素往往对应多个初级成本要素,如人工、燃料、折旧费、制造费用。
























 2704
2704

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








