自动控制原理学习记录1

Star鸭

已于 2025-04-18 18:13:11 修改

阅读量789

点赞数 32

分类专栏：自动控制原理文章标签：学习笔记自动化

于 2025-04-18 07:15:21 首次发布

本文链接：https://blog.csdn.net/Starsad/article/details/147317045

版权

自动控制原理专栏收录该内容

4 篇文章

订阅专栏

系列文章目录

【1】开闭环系统及系统稳定性分析

文章目录

前言

自动控制原理是电子信息类专业中非常重要的一个领域，它涉及到如何通过控制系统来自动调节和管理各种设备和过程。下面我将用通俗易懂的语言和例子来解释自动控制原理及其专业中的应用。

自动控制原理的基本概念

自动控制原理的核心思想是通过测量系统的输出（实际状态），与期望的目标（设定值）进行比较，然后根据这个比较结果来调整系统的输入，从而使输出达到或维持在期望的目标值。

主要组成部分：

控制对象：需要被控制的系统或设备，比如温度控制系统、速度控制系统等。
传感器：用于测量控制对象的当前状态（输出），例如温度传感器、压力传感器等。
控制器：根据传感器反馈的信息与设定值进行比较，决定如何调整输入以达到目标。常见的控制器有PID控制器。
执行器：根据控制器的指令来调整控制对象的输入，例如电机、阀门等。

通俗的例子

1. 温度控制系统

想象一下你在家里有一个空调，空调的工作就是一个典型的自动控制系统。

设定值：你希望房间的温度保持在22°C。
传感器：空调内的温度传感器实时测量房间的实际温度。
控制器：空调的控制系统会将实际温度与设定值进行比较。如果实际温度低于22°C，控制器会发出指令让空调加热；如果高于22°C，则让空调制冷。
执行器：空调的压缩机和风扇根据控制器的指令工作，调节房间的温度。

通过这个例子，你可以看到自动控制原理如何在日常生活中帮助我们维持舒适的环境。

2. 速度控制系统

另一个例子是电动机的速度控制。

设定值：你希望电动机的转速保持在1500转/分钟。
传感器：转速传感器实时测量电动机的实际转速。
控制器：控制器将实际转速与设定值进行比较。如果实际转速低于1500转/分钟，控制器会增加电动机的输入电压；如果高于1500转/分钟，则减少输入电压。
执行器：电动机的驱动电路根据控制器的指令调整电压，从而改变电动机的转速。

这个例子展示了自动控制原理在工业自动化中的应用，确保设备以稳定的速度运行。

自动控制原理在专业中的应用

作为电子信息类专业的研究生，自动控制原理在本专业多个方面都有广泛的应用：

过程控制：
在化工、食品加工等行业，自动控制系统用于监测和调节温度、压力、流量等参数，以确保生产过程的稳定性和安全性。
仪器仪表：
许多仪器（如温度计、压力计、流量计等）都采用自动控制原理来实现精确测量和控制。例如，智能温度控制仪器可以自动调节加热或冷却设备，以保持设定的温度。
机器人控制：
在机器人技术中，自动控制原理用于实现机器人的运动控制和路径规划。通过传感器反馈，控制系统可以实时调整机器人的运动轨迹，确保其按照预定路径行驶。
自动化生产线：
在现代制造业中，自动控制原理被广泛应用于自动化生产线。通过传感器和控制器，生产线可以自动调节各个环节的工作状态，提高生产效率和产品质量。
智能家居：
在智能家居系统中，自动控制原理用于实现家居设备的智能化管理。例如，智能灯光系统可以根据环境光线自动调节亮度，提升居住舒适度。

小结

自动控制原理是通过测量、比较和调整来实现对系统的自动管理和控制。它被广泛应用于过程控制、仪器仪表、机器人技术、自动化生产线和智能家居等领域。掌握自动控制原理将帮助你设计和优化各种自动化系统，提高工作效率和系统性能。

提示：以下是本篇文章正文内容，下面案例可供参考

一、动态系统建模与分析

1.1 流体系统

进口流量q_in、容器横截面积A、出口流阻R，需要知道液面高度h的动态方程（dh/dt）=？

先说说流体系统中几个基本元素，这里所说均是不可压缩均质流体：

压强：（1）重力产生的压强叫静压，（2）绝对压强等于大气压强+液体静压，（3）表压：测量出来的压强,即绝对压强与参考压强的差。

流阻：流体流动时管道等阻碍流动，这时就会产生压差（与流量相关，每秒钟通过流体的质量，单位kg/s），与电阻概念类似。理想压源：Ps，（如压缩机，泵）。

质量守恒定律：如果容器有进有出，那容器内部流体质量变化（dm/dt）一定等于流进的质量m_in减去流出质量m_out，两边同除密度得到体积变化dv/dt等于进入流量q_in减去流出流量q_out。体积V=Ah，从压力角度分析，假如大气压Pa，某一点压力为P。

有了以上基本知识，回到最初问题：液面高度h的动态方程（dh/dt）=( q_in / A ) - (gh / AR)

1.2 传递函数

本小节剖析用传递函数分析系统表现的核心所在，这对今后学习不管经典控制理论、根轨迹、伯德图或者是对信号处理都有很大帮助，可以说后者都是从传递函数这一点伸展出去的。

我们从前面的流体建模例子开始，对液面高度h的动态方程化简，

令 A = 1，然后定义系统输出 X = h，系统输入 U = q_in ,化简分析对时间的函数，为了简化引入拉普拉斯变换，假定零初始状态，即X(0) = 0，得到系统传递函数G(s) = X(s) / U(s) =1 / (s+g/R)

化成系统框图形式我们发现 U(s)G(s) = X(s) ，这就把原来卷积关系变成了乘法的关系。像这类系统，输入与输出关系基本都为卷积关系，就好比你受到一系列暴击，上一次创伤还没抚平，下一次又给你叠加上去了，这个叠加过程就是卷积，卷积计算很麻烦，拉氏变换把卷积变成乘积。

下面我们看看如何分析：假定系统输入U(t)为常数C

因为左右等式分子为1，我们令s = 0，s = -g / R 得到系数 A,B，此时就得到系统输出的拉氏变换 X(s)，对其逆变换就得到时域函数 X(t)

这是一个典型的一阶系统响应，现在我们来看此系统关键点在哪？其实关键点就在 e 的指数部分

0t 表明它不会变，(-g/R)t 表明随着时间在不断衰减，所以说整个系统是稳定的，也就是说它一定在某个范围内不会变到无穷。如果细心就会发现，这俩系数还出现在下式分母部分

令其分母为零时，得到 s1、s2 俩极点值

有了这个概念，我们就可以理解经典控制系统的一个控制理念了，就是通过设计不同的系统输入U，令 U(s) * G(s) ,这个时候去配置系统的极点，让极点到一个我们希望它到的地方，从而达到控制系统输出 X(t) 的目的。

1.3 非零条件下传递函数

以下面这个一阶系统为例

传递函数 G(s) = X(s) / U(s) = 1/s+a，拉式逆变换列出 x(0) = 0 微分方程

当 x(0) ≠ 0 时，传递函数分母多出一项 x(0)

这样我们就得出 x(0) ≠ 0 时，传递函数写出形式是在输入端加入幅度为 x(0) 的冲击，但他并不会影响系统稳定性。

二、自动控制原理

2.1 开环系统、闭环系统与反馈系统

我们以前面流体系统为例展开，输出从0时刻开始缓慢增加，最后收敛到 CR/g 这个高度，如图所示：
假如系统此时控制目标高度h由x趋向x_d ，就可以得到输入C （开环控制）

闭环框图如下：

进一步简化：

得到一个新的传递函数，将其用框图表示得到 V 和 S 之间的开环，从这开始我们研究方向变成新闭环系统传递函数，里边的 D 就是我们要设计的控制器，也是我们研究的重点，可以从这入手，通过不同控制方法，做系统稳定性分析，误差分析等等

2.2 稳定性分析——极点

稳定性在自控中是一个很重要的概念，是控制系统的基础，在此基础上才有瞬态分析、稳态误差分析、控制优化等

我们都知道系统稳定就是传递函数极点在复平面左半部分，那具体是啥意思呢？

先看稳定的定义，假如有一轨道选取 A B C 三个位置点（平衡点），B点光滑，C有摩擦，三点都放小球都可以保持静止不动，数学表达dx/dt = 0

若小球位置偏移，A点小球随时间不再回到A， B点无摩擦左右摇摆，C点有摩擦最终会停在C点。

则 A—不稳定 / B—临界稳定 / C—稳定

对于控制系统要明确分析对象。从系统函数剖析，前面开分析了开环闭环传递函数如下,我们在研究系统稳定性时，一般会输入一个单位冲激响应（宽度为0面积为1理想函数），例如拿你43号大脚踢小球，足够快、有力。

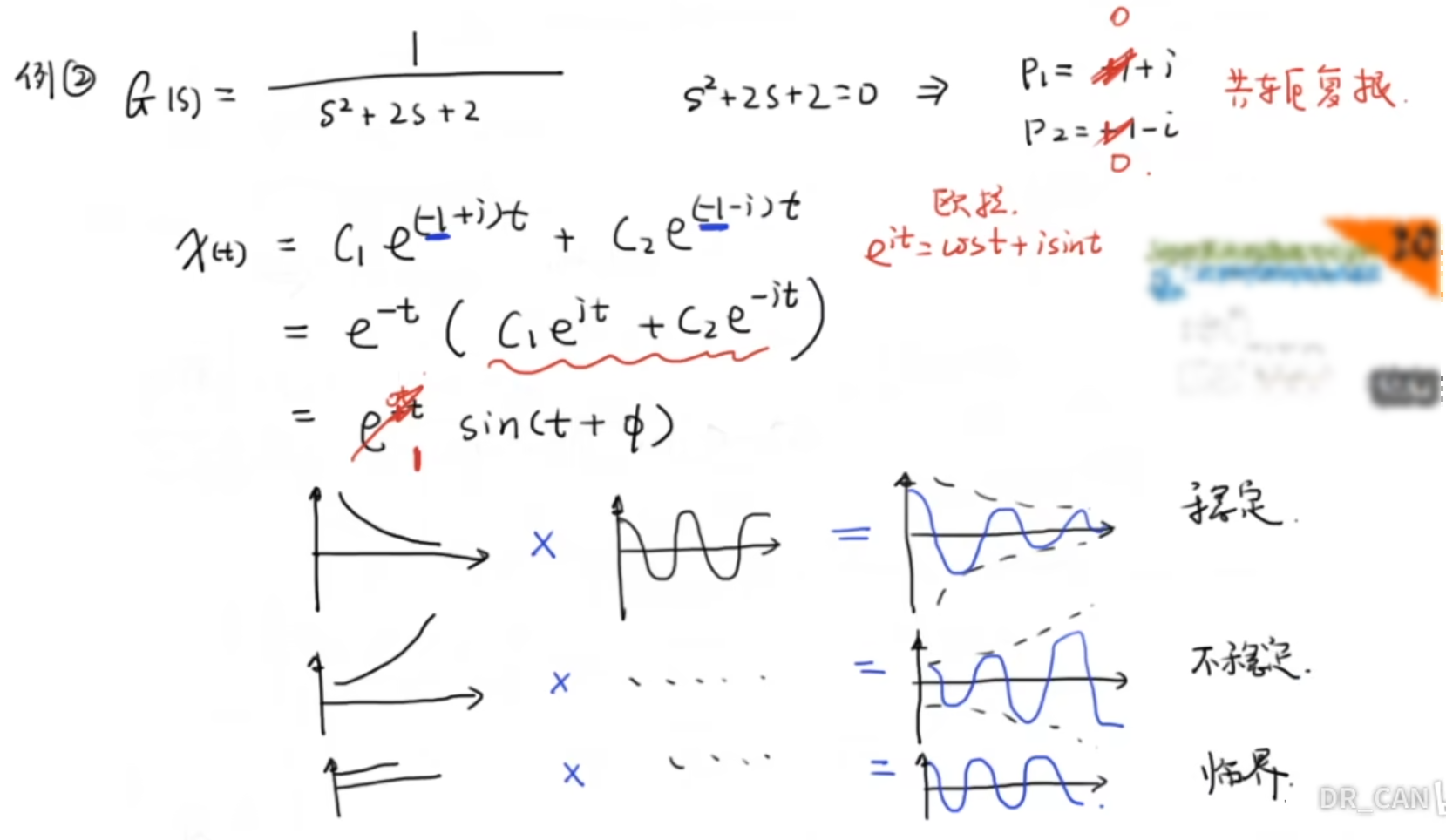
接下来看判断稳定性例子：

稳定：实部<0 不稳定：实部>0 临界稳定：实部=0

结论：系统稳定就是传递函数极点在复平面左半部分。所以在控制系统中设计控制器 D 时就会有目标：使极点在左半平面（即极点配置）——经典控制理论的核心设计思路

总结

本文通过对流体系统建模引入系统传递函数，从而分析系统稳定性，学会了理论与经典控制系统系统设计相联系。学习内容来自大佬DR_CAN