
笔记整理:刘一春,天津大学硕士
论文链接:https://arxiv.org/pdf/2205.10128.pdf
动机
在知识图上回答复杂的一阶逻辑(FOL)查询是多跳推理的基本任务。传统的符号方法遍历一个完整的知识图来提取答案,这为每一步提供了良好的解释。最近的神经方法学习复杂查询的几何嵌入。这些方法可以推广到不完备知识图,但它们的推理过程很难解释。在本文中,我们提出了图神经网络查询执行器(GNNQE),这是一种兼具两者优点的神经符号模型。GNN-QE将复杂的FOL查询分解为模糊集上的关系投影和逻辑运算,为中间变量提供可解释性。GNN-QE采用知识图补全的图神经网络来进行关系映射,并用乘积模糊逻辑对逻辑运算进行建模,对缺失链进行推理。在3个数据集上的大量实验表明,GNN-QE在回答FOL查询方面明显优于以往的最新模型。同时,GNN-QE可以在没有显式监督的情况下预测答案的数量,并提供中间变量的可视化。
亮点
GNN-QE的亮点主要包括:
(1)提出了在知识图谱上回答复杂一阶逻辑问题的新方法—— GNN-QE。
(2)解决模型只能适应于完整的知识图谱,不能在测试的时候泛化到不完整的知识图谱的困难。
(3)解决对FOL表达式进行批处理的困难。
概念及模型
GNN-QE中主要由三部分构成
(1)Symbolic Query Decomposition:给定FOL查询,第一步是将其转换为基本运算的表达式,以便我们可以通过执行该表达式来检索答案。
(2)NBFnet:为了解决不完备知识图上的复杂查询,我们学习了一个神经模型来执行关系投影Pq(X)。
(3)Fuzzy Logic Operations:逻辑运算(即,C(x,y),D(x,y),N(X))将多个关系投影结果粘合在一起,并为下一个关系投影生成输入模糊集。
模型整体框架如下:
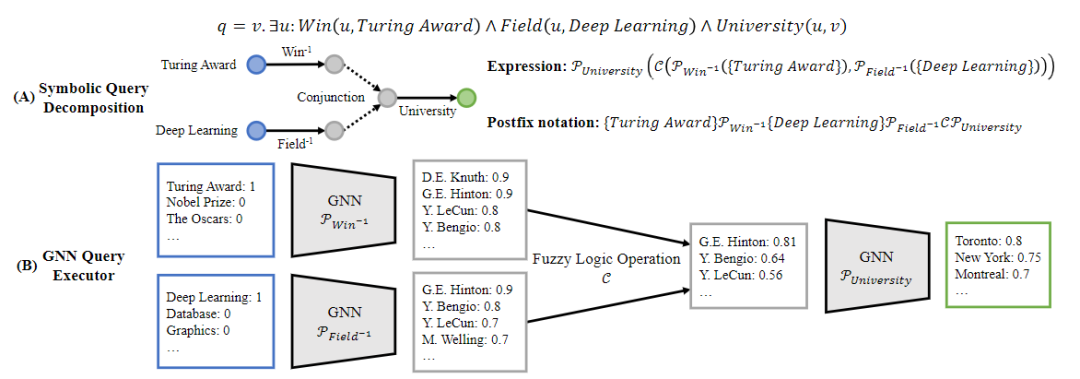
从自然语句到输入模型的逻辑表达式

①本文从FOL查询语句开始运算,给出自然语句是为了方便理解。
②这里采用了模糊推理的方法,定义了模糊集上的四种操作符(关系映射,合取,并取,非),通过这些操作符将查询语句转换成表达式。
③这里是因为如果不做处理,机器需要递归地解析括号,并从内到外执行表达式,给批次处理带来很大困难。以前的工作都是对每一种查询结构分批处理,这里的创新点在于,将其转化为后缀表达式,不用递归,用堆栈就可以轻松解决每种结构的表达式。
NBFnet(关系映射)
(1)Indicator:若u=v,也就是长度为0的路径表示h0等于message操作的幺元,若u!=v,u和v之间没有长度为0的路径,则仅是作为一个边界,是aggregate操作的幺元。
(2)message:将已有的路径与新边连接,最终成为一条连接u和v的可用路径。常用的有transe,distmult等。
(3)aggregate:将所有长度的路径融合在一起作为路径的整体表示。常用用的有:sum,mean,max等。

逻辑模糊操作
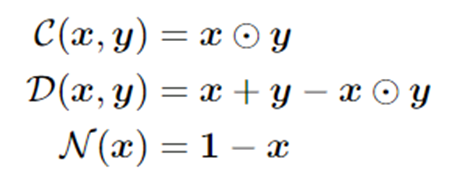
这样设置是为了满足德摩根定律:
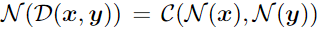
遍历丢弃
训练GNN-QE的一个挑战是让模型在测试时推广到不完整的KG。这是因为所有的训练查询都是通过假设训练图是完整的来生成的。换句话说,所有的训练查询都可以通过训练图上的一个简单的关系遍历模型来完美地求解,而不需要对任何缺失的链接进行建模。GNN模型可以很容易地发现这种模式,它不会在测试时推广到不完整的知识图。
为了解决这个问题,本文引入了遍历丢弃来在训练时创建一个不完整的KG。具体地说,本文首先运行关系遍历模型来提取与查询对应的所有边。然后,本文以概率p随机地掩蔽出每个关系投影中被遍历的边。直观地说,概率p在简单的关系遍历模型和完整的推理模型之间权衡。如果p较小,则GNN模型可能收敛到平凡关系遍历模型,否则将被迫编码非平凡推理特征。由于测试查询中的一些边可能存在于KG中,因此使用大的p来阻止关系遍历模型并不总是最优的。
理论分析
实验
作者采用了3个公开数据集进行实验,分别是:FB15k,FB15k-237,NELL-995。Baselines有嵌入模型GQE,Q2B,BetaE,FuzzQE,ConE,神经符号模型CQD-CO,CQD-Beam,评价指标MRR。
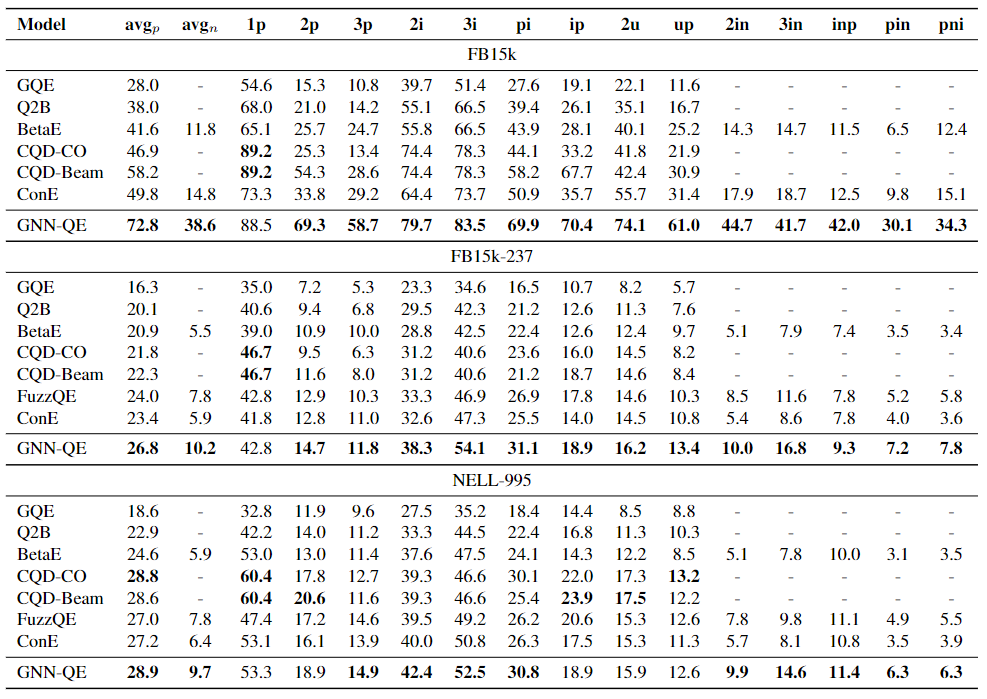
我们观察到,GNN-QE对于EPFO查询和在所有3个数据集上进行否定的查询都获得了最好的结果。值得注意的是,GNN-QE在AVGP中实现了22.3%的平均相对增益,在AVGN中实现了95.1%的平均相对增益。我们将这一收益归因于模糊集相对于几何嵌入的优势。
下面显示了本文的模型预测与基本事实之间的平均绝对百分比误差(MAPE)。注意:如果没有明确的监督,现有的方法都不能预测答案的数量。

下面是不同查询结构下在FB15k-237上的模型预测结果和基本事实答案数量之间的排名相关性。

我们可以观察到GNN-QE在所有查询类型上的性能都远远超过现有方法。
总结
本文提出了一种新的神经符号模型,即图神经网络查询执行器(GNN-QE),用于回答不完备知识图上的复杂FOL查询。该方法将复杂查询分解为模糊集上基本操作的表达式,并利用学习的GNN关系投影模型和模糊逻辑运算来执行该表达式。GNN-QE不仅在3个数据集上显著优于以前最先进的模型,而且还提供了对中间变量的可解释性。未来的工作可能会将GNN-QE与解析器结合起来,以回答自然语言形式的逻辑查询。
OpenKG
OpenKG(中文开放知识图谱)旨在推动以中文为核心的知识图谱数据的开放、互联及众包,并促进知识图谱算法、工具及平台的开源开放。

点击阅读原文,进入 OpenKG 网站。





















 652
652











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








