人工智能/机器学习基础知识——损失函数

Loss Function（损失函数）

以某种方式计算输出值（预测值）与真实值之间的误差，误差值是反向传播的起点

分类（Classification）

Kullback-Leibler Divergence（Relative Entropy）

CSDN

CSDN

KL散度（相对熵）

• 公式为：
  $$D_{KL}(p||q)=\sum _{i=1}^{N}p(x_i)\log \frac{p(x_i)}{q(x_i)}=E[\log \frac{p(x)}{q(x)}]$$
  其中，$N$为类别总数，$p(x)$为目标分布（Label），$q(x)$为预测分布（Predict）

• KL散度只有在$p(x)$，$q(x)$分布完全一致时才等于0，其余时候都大于0。（证明见链接）

• 一个例子：假设目标分布为
  $$p(x)=[0.95,0.05]$$
  预测分布为
  $$q(x)=[0.8,0.2]$$
  那么
  $$D_{KL}(p||q)=0.95\times \log \frac{0.95}{0.8}+0.05\times \log \frac{0.05}{0.2}$$

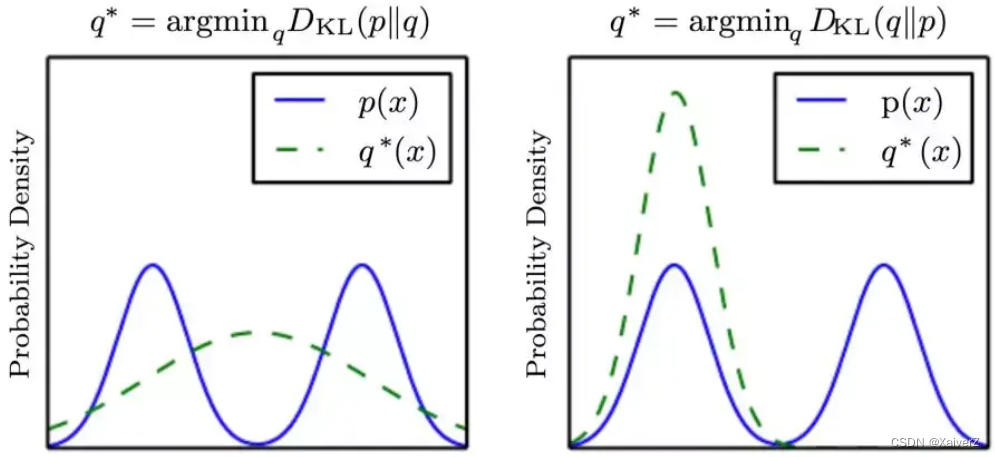
• KL散度是一种非对称的散度，在计算两种分布$p$，$q$之间的KL散度时（假设用分布$q$去近似分布$p$，且$p$为混合高斯分布，$q$为高斯分布），按照顺序的不同，有两种KL散度，假设分布为连续的，则采取微积分可定义为

  • 前向KL散度

    Forward KL divergence

    Moment projection（M-Projection）

    $$\mathrm{KL}\left(p,q\right)=\int p(\mathbf{x})\log \frac{p(\mathbf{x})}{q(\mathbf{x})}\mathrm{d}\mathbf{x}$$

    • 当$p(x)\to 0$，$q(x)>0$时，KL散度为$0$

    • 当$p(x)>0$，$q(x)\to 0$时，KL散度趋于无穷大

    • 上面两种极端情况表达的含义是，在$p(x)$大于$0$的区域（即有分布的区域），若$q(x)$趋近于$0$，则KL散度会非常大，即KL散度对这种情况很敏感，$q(x)$会尽量避免这种情况，使其在$P(x)$大于$0$的区域也都大于$0$（即有分布）；另一种情况，在$p(x)$趋于0的区域（即无分布的区域），若$q(x)$大于$0$，则KL散度为$0$，KL散度对这种情况并不敏感。综上，为了保证KL散度最小，$q(x)$会“高估”$p(x)$的值域，除了$p(x)$的区域以外，其余近邻区域也会有部分分布

  • 逆向KL散度

    Reverse KL divergence

    Information Projection（I-Projection）

    $$\mathrm{KL}\left(q,p\right)=\int q(\mathbf{x})\log \frac{q(\mathbf{x})}{p(\mathbf{x})}\mathrm{d}\mathbf{x}$$

    • 当$p(x)\to 0$，$q(x)>0$时，KL散度趋于无穷大

    • 当$p(x)>0$，$q(x)\to 0$时，KL散度为$0$

    • 上面两种极端情况表达的含义正好与前向KL散度相反，在$p(x)$大于$0$的区域（即有分布的区域），若$q(x)$趋近于$0$，则KL散度为$0$，即KL散度对这种情况不敏感；另一种情况，在$p(x)$趋于0的区域（即无分布或分布稀疏的区域），若$q(x)$大于$0$，则KL散度趋于无穷大，即KL散度对这种情况很敏感，所以$q(x)$在$p(x)$无分布的区域也都无分布。综上，为了保证KL散度最小，$q(x)$不会像前向KL散度那样“高估”$p(x)$的值域，反之，$q(x)$的分布会严格的限制在$p(x)$的分布区域内；若$p(x)$分布区域中存在稀疏区域，那么$q(x)$为了避免第一种情况，则有可能会“低估”$p(x)$的值域

Jensen-Shannon Divergence

JS散度

• JS散度基于KL散度作出改进

  $$D_{JS}(p||q)=\frac{1}{2}{D}_{KL}(p||M)+\frac{1}{2}{D}_{KL}(q||M),M=\frac{1}{2}(p+q)$$

• JS散度是对称的且取值在$[0,\log 2]$

• 当两个分布越接近时，JS散度的值越小；当两个分布完全相同时，其JS散度为0。但JS散度存在一个问题，当两个分布完全不相关不重叠（或有部分可忽略的小范围重叠）时，JS散度的值为一个常数。

  • 由$KL\left(P_1\Vert P_2\right)={\mathbb{E}}_{x\sim P_1}\log \frac{P_1}{P_2}$与$JS\left(P_1\Vert P_2\right)=\frac{1}{2}KL\left(P_1\Vert \frac{P_1+P_2}{2}\right)+\frac{1}{2}KL\left(P_2\Vert \frac{P_1+P_2}{2}\right)$可知，当两个分布$P_1$，$P_2$无重叠或重叠部分可忽略时，有如下四种情况

    • $P_1(x)=0,P_2(x)=0$

    • $P_1(x)\ne 0,P_2(x)\ne 0$

    • $P_1(x)=0,P_2(x)\ne 0$

    • $P_1(x)\ne 0,P_2(x)=0$

  • 第一种情况下JS散度为$0$；第二种情况由于重叠可忽略所以JS散度也为$0$；第三种情况JS散度为$\log 2$；第四种情况类似JS散度为$\log 2$

  • 所以，当两个分布完全不重叠时，JS散度为常数$\log 2$

Wasserstein Distance（Earth-Mover Distance）

Wasserstein距离（推土机距离）

• 对于两个分布$p$、$q$，它们之间的（1st）Wasserstein Distance为

  $$W\left(p,q\right)=\underset{\gamma \sim \Pi \left(p,q\right)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]$$
  其中$\Pi \left(p,q\right)$是$p$与$q$的联合分布的集合。

  • 上式说明，对于每一个可能的联合分布$\gamma$，可以从中采样$(x,y)\sim \gamma$分别得到$p$与$q$分布中的样本$x$与$y$，并计算出这对样本的距离$\Vert x-y\Vert$，写成期望形式即${\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]$。而在所有可能的联合分布中对期望取下界，即可得到Wasserstein Distance的表达式

• Wasserstein距离相比KL散度、JS散度的优越性在于，即便两个分布没有重叠，Wasserstein距离仍然能够反映它们的远近

• 考虑如下二维空间中的两个分布$p$与$q$，分别在线段$AB$与$CD$上均匀分布，$\theta$表示它们之间的距离

  

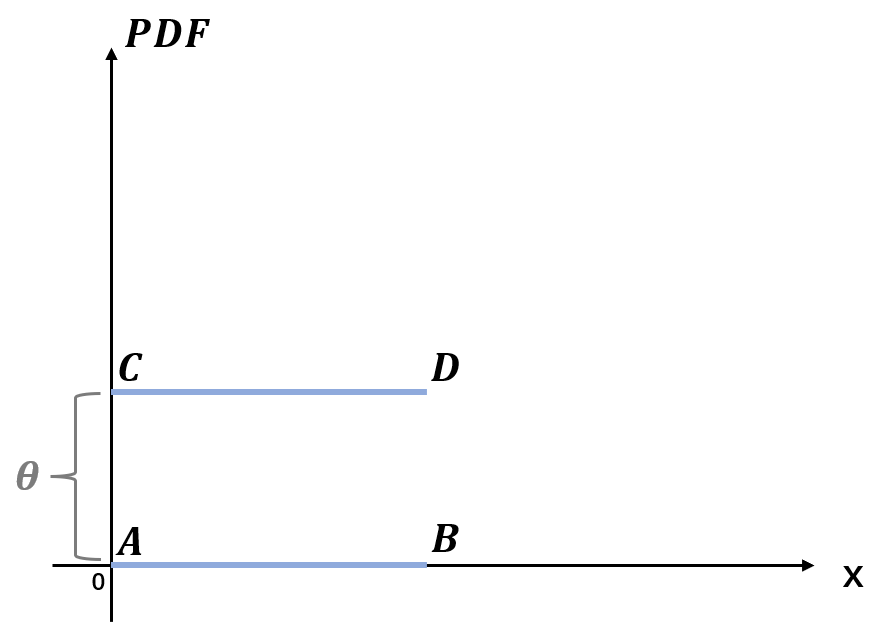
  • 若使用KL散度作为度量

    $$KL\left(p\Vert q\right)=KL\left(p\Vert q\right)=\{\begin{array}{ll}+\infty & \text{ if }\theta \ne 0\\ 0& \text{ if }\theta =0\end{array}$$

  • 若使用JS散度作为度量

    $$JS\left(p\Vert q\right)=\{\begin{array}{ll}\log 2& \text{ if }\theta \ne 0\\ 0& \text{ if }\theta =0\end{array}$$

  • 若使用Wasserstein距离作为度量

    $$W\left(p,q\right)=|\theta |$$

• 可以看到，KL散度与JS散度关于距离$\theta$要么不可导，要么导数为0；而Wasserstein距离关于距离$\theta$却是（几乎）处处可导且导数不为0的。若采用梯度下降法去优化$\theta$这个参数，那么KL散度与JS散度完全提供不了梯度，但是Wasserstein距离却可以提供有意义的梯度

Hinge Loss

博客园

用于最大间隔分类（Maximum-margin Classification），如SVM

对于多分类

• 公式为：
  $$L=\sum _{j\ne y_i}\max (0,s_j-s_{y_i}+1)$$
  其中，$s_j$是其他标签的预测值，$s_{y_i}$是目标标签的预测值

• 一个例子：一个样本经过NN后输出
  $$s=[3.4,5.6,1.2]$$
  其中，该样本的标签索引为0。则
  $$L=\max (0,5.6-3.4+1)+\max (0,1.2-3.4+1)$$

Cross Entropy（交叉熵）

知乎

简书

PyTorch官方文档

用于分类问题。以下所有内容均在PyTorch上实际验证过。

• 交叉熵向量化表述例子：$$Output=[0.1,0.3,0.4,0.2]$$ $$Label=[0,1,1,0]$$
  Label一般在框架内部转换成独热码形式，输入时直接按照Label的量化值输入即可。

• 实际上，各框架交叉熵损失函数的输入可以有多种形式，例如硬标签、软标签等等，需视具体情况而定。

二分类（Binary Cross Entropy）

BCE

• 公式为：
  $$-L=y\cdot \log p+(1-y)\cdot \log (1-p)$$
  其中， $y$为标签，$p$为概率值

• 例子：（batch_size=2）输出概率矩阵$[[0.9],[0.6]]$，对应的Label为$[[1],[0]]$。

  • 计算第一个样本的损失：
    $$-L_1=1\cdot \log 0.9+(1-1)\cdot \log (1-0.9)$$
  • 计算第二个样本的损失：
    $$-L_2=0\cdot \log 0.6+(1-0)\cdot \log (1-0.6)$$
  • 平均batch内所有样本的损失：
    $$L=\frac{L_1+L_2}{2}$$

多标签分类（Binary Cross Entropy）

BCE

• 公式为：
  $$-L=\frac{\sum _i^c{y}_i\cdot \log p_i+(1-y_i)\cdot \log (1-p_i)}{c}$$
  其中， $y_i$为标签，$p_i$为概率值，$c$为类别总数

• 例子：（batch_size=2）输出概率矩阵$[[0.9,0.6,0.7],[0.5,0.8,0.3]]$，对应的Label为$[[1,0,1],[0,1,0]]$。

  • 计算第一个样本的损失：
    $$-L_{1_1}=1\cdot \log 0.9+(1-1)\cdot \log (1-0.9)$$
    $$-L_{1_2}=0\cdot \log 0.6+(1-0)\cdot \log (1-0.6)$$
    $$-L_{1_3}=1\cdot \log 0.7+(1-1)\cdot \log (1-0.7)$$
    对每个标签的损失取平均值：
    $$L_1=\frac{L_{1_1}+L_{1_2}+L_{1_3}}{3}$$
  • 计算第二个样本的损失：
    $$-L_{2_1}=0\cdot \log 0.5+(1-0)\cdot \log (1-0.5)$$
    $$-L_{2_2}=1\cdot \log 0.8+(1-1)\cdot \log (1-0.8)$$
    $$-L_{2_3}=0\cdot \log 0.3+(1-0)\cdot \log (1-0.3)$$
    对每个标签的损失取平均值：
    $$L_2=\frac{L_{2_1}+L_{2_2}+L_{2_3}}{3}$$
  • 平均batch内所有样本的损失：
    $$L=\frac{L_1+L_2}{2}$$

• 多标签分类实际上二分类的叠加：一个样本有多个标签相等于对每一个标签做一次二分类，所以多标签分类需要对每一个标签进行交叉熵计算损失

• 在PyTorch中，可以通过指定$weight$参数来对每个Label（类别）赋予不同的权重

多分类（Cross Entropy）

CE

• 公式为：
  $$L(x,class)=-\log (\frac{\exp (x[class])}{\sum _j\exp (x[j])})=-x[class]+\log (\sum _j\exp (x[j]))$$
  其中，$x$为输出的Logits值，非概率，$class$为该样本对应的label值。

• 例子：（batch_size=2）输出Logits矩阵$[[1.3,1.2,1.1],[0.6,1.6,1.7]]$，对应的Label为$[2,1]$，独热码为$[[0,0,1],[0,1,0]]$。

  • 计算第一个样本的损失：
    $$L_1(x_1,2)=-\log (\frac{\exp 1.1}{\sum _j\exp (x_1[j])})=-1.1+\log (\sum _j\exp (x_1[j]))$$
  • 计算第二个样本的损失：
    $$L_2(x_2,1)=-\log (\frac{\exp 1.6}{\sum _j\exp (x_2[j])})=-1.6+\log (\sum _j\exp (x_2[j]))$$
  • 平均batch内所有样本的损失：
    $$L=\frac{L_1+L_2}{2}$$

• 实际上，对于如下一组数据：
  $$Output=[0.1,0.3,0.4,0.2]$$ $$Label=[0,1,0,0]$$
  若该任务为多分类任务，那么仅需根据二分类交叉熵公式计算正确类别的那组数据：
  $$L=-1\cdot \log 0.3-(1-1)\cdot \log (1-0.3)$$
  若该任务为多标签分类任务，那么需要根据二分类交叉熵公式计算所有的数据：
  $$L_1=-0\cdot \log 0.1-(1-0)\cdot \log (1-0.1)$$
  $$L_2=-1\cdot \log 0.3-(1-1)\cdot \log (1-0.3)$$
  $$L_3=-0\cdot \log 0.4-(1-0)\cdot \log (1-0.4)$$
  $$L_4=-0\cdot \log 0.2-(1-0)\cdot \log (1-0.2)$$
  最后再将该样本的损失取平均：
  $$L=\frac{L_1+L_2+L_3+L_4}{4}$$
  这就是多标签分类和多分类的重要区别

• 其实还可以从另一个角度理解多分类与多标签分类的区别：对一个样本来说，多分类只需要给该样本赋上一个标签即可，所以只需算该组标签的损失值。而多标签分类需要给样本赋上多个标签，每个标签都需要检验是否为该样本的一个标签，所以需要计算所有的损失值。

• Tips：多分类只计算正确标签的那一组损失值，而多标签分类则计算所有的损失值。在PyTorch中，多分类的Target Label输入为一维Tensor，且Label值为量化值，非独热码。经过PyTorch测试，多分类通过直接修改Label值不能应用Label Smooth，而多标签分类与二分类是可以的。

• 在PyTorch中，可以通过指定$weight$参数来对每个Label（类别）赋予不同的权重

Class Weight

Class Weight

• 样本数倒数

  $$\frac{1}{\text{ ClassSize }}$$

• Inverse Category Frequency（ICF）

  $$\mathrm{icf}\left(t_i\right)=\log \left(\frac{|C|}{cf\left(t_i\right)}\right)$$
  其中，$|C|$为样本总数，$cf(t_i)$表示第$t_i$类样本的频数

• 类别最大样本数量 / 每个类别样本数量

  • 例子：三个类别样本数分别为$100000,100,10$，则权重系数为：

  $$\text{ weight }=\left[\frac{100000}{100000},\frac{100000}{100},\frac{100000}{10}\right]=[1.0,1000,10000]$$

α-balanced Cross Entropy

Cross Entropy的改进，针对二分类和多标签分类，解决正负样本不均衡问题

• 将二分类公式简化为：
  $$p_t=\{\begin{array}{ll}p,& y=1,\\ 1-p,& otherwise,\end{array}$$
  $$CE(p,y)=CE(p_t)=-\log (p_t)$$

• 对于一个二分类任务来说，如果正样本（即Label为1）或负样本（即Label为0）占比过大的，会诱导模型朝过采样的一方学习，对欠采样的一方性能很差。
  $${\alpha }_t=\{\begin{array}{ll}\alpha ,& y=1,\\ 1-\alpha ,& otherwise,\end{array}$$
  其中，$\alpha \in [0,1]$，为超参数。通过给标准交叉熵乘上α-balanced权重${\alpha }_t$，可以对过采样的一方赋予一个比较小的权重和，欠采样一方赋予一个较大的权重，达到改善正负样本不均衡的目的。
  $$CE(p_t)=-{\alpha }_t\log (p_t)$$

• α-balanced并未解决类别不均衡问题，它解决的是正负样本不均衡问题。严格来说，多分类问题中只存在类别不均衡问题，即在所有的类别中，有的类别样本特别多，有的特别少。但对于一个多标签分类任务来说，也存在正负样本不均衡（把每个类别都看作是一个独立的二分类任务），即对每一个类别来说，“是与不是该类别的样本严重失衡”；从另一个角度看多标签分类任务，有的类别多，有的类别少，这也会影响模型学习。类别不均衡可通过设置$weight$参数解决。其实，在多标签分类任务下，解决正负不均衡问题在一定程度上也缓解了类别不均衡问题。

Focal Loss

Paper : Focal Loss for Dense Object Detection

用于目标检测中正负样本不均衡问题，而非类别不均衡。

• 公式为：
  $$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }\log (p_t)$$
  其中，${\alpha }_t$与$p_t$详见α-balanced Cross Entropy，$\gamma$为超参数正整数。

• 对于一个二分类任务来说，如果正负样不均衡的话，会导致模型朝过采样的那一方偏离。在Focal Loss中，若$p_t$越大，则$1-p_t$越小，也就是说给简单样本的那一方赋予一个更小的权重，让模型更聚焦于学习那些困难样本。${\alpha }_t$是用来调整正负样本的比例的，例如正样本给0.25，负样本给0.75。

• Focal Loss本质还是属于困难样本挖掘领域，注意样本少的类别≠困难样本，困难样本指学习难度大，较难学习的那些样本，这与样本少的类别不是同一个概念，Focal Loss改善的是困难样本的效果，而不是少类样本的效果。将Focal Loss用于易于学习的类别上可能会导致效果下降。

Equalized Focal Loss

Paper : Equalized Focal Loss for Dense Long-Tailed Object Detection

EFL

回归（Regression）

简书-回归损失函数

MAE（平均绝对误差-L1损失函数）

用于回归问题

• 公式为：$$MAE=\frac{\sum _{i=1}^n|y_i-y_i^p|}{n}$$其中，$n$为样本数，$y_i$为样本真实值，$y_i^p$为模型对于该样本的预测值

MSE（均方误差-L2损失函数）

用于回归问题

• 公式为：$$MSE=\frac{\sum _{i=1}^n(y_i-y_i^p{)}^2}{n}$$其中，$n$为样本数，$y_i$为样本真实值，$y_i^p$为模型对于该样本的预测值

RMSE

Root Mean Square Error

• 公式为：

  $$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left({\hat{y}}_i-y_i\right)}^2}$$

Huber（平滑平均绝对误差）

Huber Loss

• 公式为：

  $$L_{\delta }(y,f(x))=\{\begin{array}{ll}\frac{1}{2}(y-f(x){)}^2& \text{ for }|y-f(x)|\le \delta \\ \delta |y-f(x)|-\frac{1}{2}{\delta }^2& \text{ otherwise }\end{array}$$
  当损失小于阈值$\delta$时，使用MSE计算损失；当损失大于阈值$\delta$时，使用MAE计算损失

• Huber Loss降低了对异常点（离群点）的惩罚程度，对异常值的敏感性较差

Log-Cosh

Quantile Loss（分位数损失）