四元数，欧拉角，旋转矩阵，旋转向量

GondorFu

已于 2023-12-08 14:22:58 修改

阅读量1.2k

点赞数 8

CC 4.0 BY-SA版权

分类专栏：数学基础文章标签：矩阵线性代数

于 2023-12-08 11:42:20 首次发布

本文链接：https://blog.csdn.net/a40850273/article/details/134869606

数学基础专栏收录该内容

7 篇文章

订阅专栏

本文介绍了欧拉角在三维旋转中的表示及其问题，如万向锁，以及四元数和旋转向量作为替代方案的使用方法，包括Python库scipy和pyquaternion的示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

四元数，旋转矩阵，旋转向量，欧拉角

一、欧拉角

1、欧拉角是表达旋转的最简单的一种方式，形式上它是一个三维向量，其值分别代表物体绕坐标系三个轴(x,y,z轴）的旋转角度，默认旋转正向为逆坐标轴逆时针方向。

2、在旋转过程中，xyz轴方向并不是固定不变的，而是随着前面的旋转而改变。比如如果绕 x 轴旋转 90 度，那么旋转后的 y 轴正向将指向原始的 z 轴方向，而旋转后的 z 轴正向将指向 y 轴负向。由此可以看出，欧拉角对应的具体旋转与 xyz 轴的旋转顺序是有关的，相同的 xyz 旋转角度，如果按 xyz 的顺序进行旋转使用按 zyx 的顺序进行旋转，得到的结果是不一致的。

3、在具体应用中，xyz 轴朝向不固定，需要具体情况具体分析。

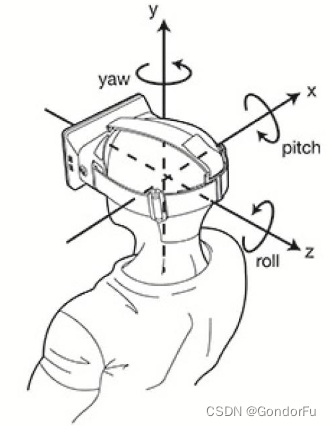
pitch：绕 x 轴旋转，
yaw：绕 y 轴旋转，
roll：绕 z 轴旋转，

4、欧拉角表示最大的问题是存在万向锁问题。万向锁（Gimbal lock）是在使用动态欧拉角表示三维物体的旋转时出现的问题。一旦选择±90°作为pitch角，就会导致第一次旋转和第三次旋转等价，整个旋转表示系统被限制在只能绕竖直轴旋转，丢失了一个表示维度。

二、四元数

四元数通过四个实数描述三维旋转， $q=w+ix+jy+kz$ ，其中 $w^2+x^2+y^2+z^2=1$ 。

三、旋转向量

旋转向量用一个三维向量来表示三维旋转变换，该向量的方向是旋转轴，其模则是旋转角度。

转换方法

一、scipy.spatial.transform.Rotation

官方文档：

https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.transform.Rotation.html#scipy.spatial.transform.Rotation

from scipy.spatial.transform import Rotation as R

# 从四元数加载
r = R.from_quat([0, 0, np.sin(np.pi/4), np.cos(np.pi/4)])

# 从旋转矩阵加载
r = R.from_matrix([[0, -1, 0],
                   [1, 0, 0],
                   [0, 0, 1]])

# 从旋转向量加载
r = R.from_rotvec(np.pi/2 * np.array([0, 0, 1]))

# 从欧拉角加载
r = R.from_euler('zyx', [
[90, 0, 0],
[0, 45, 0],
[45, 60, 30]], degrees=True)

# 使用四元数表示
r.as_quat()

# 使用旋转矩阵表示
r.as_matrix()

# 使用旋转向量表示
r.as_rotvec()

# 使用欧拉角表示
r.as_euler('zyx', degrees=True)


# 取逆
inv_r = r.inv()

# 对点进行旋转
r.apply(v)

二、pyquaternion.Quaternion

官方文档：https://kieranwynn.github.io/pyquaternion/

r = Quaternion([w, x, y, z]).rotation_matrix

旋转矩阵和平移向量的特殊操作

如果给定 A2B 的旋转矩阵和平移向量，但是需要 B2A 的旋转矩阵和平移向量，可以如此操作：

R_B2A = np.linalg.inv(R_A2B)
T_B2A = -np.dot(R_A2B, T_A2B)