自动出价下机制设计系列 (二) ： 面向私有约束的激励兼容机制设计

本文作者：真柏、妙临

欢迎关注：阿里妈妈技术公众号>>

导读：这篇是阿里妈妈在自动出价下机制设计系列的第二篇工作（🔗 第一篇：面向异质目标函数广告主的拍卖机制设计）。在自动出价中，广告主的诉求以及与平台交互的模式发生了明显的变化。其中最值得关注的特点之一，是广告主的决策内容从具体的流量出价变成了对出价算法的设置调整。我们考虑了出价设置中最常见的两个约束，预算与投资回报率（ROI），推导相应的激励兼容条件，即在怎样的拍卖机制下广告主上报真实约束就可以最大化自身的利益，并进一步设计可实现的激励兼容机制。

▐ 摘要

自动出价已经成为在线广告拍卖的流行范式。不同于传统的手动竞价，自动出价中的广告主在一个周期内对多次广告拍卖进行累积的广告效果评估，并且拥有私有的经济约束。基于这些新的特点，我们考虑了适用于自动出价的拍卖模型：广告主将预算和投资回报率（ROI）等经济约束作为私有信息，且优化长期累积的广告效果。我们针对这种多维设定，从私有约束的角度推导了激励兼容的条件，并展示了任何可行的分配规则都可等效地简化为关于预算的一系列非递减函数。然而，从这些非递减函数映射而来的分配通常呈现出不规则的形状，这使得很难将机制设计目标闭式表达。为了克服这一设计难题，我们提出了一系列基于个性化排序函数且灵活、易实现的激励兼容自动出价拍卖，借鉴常见的广义第二价格（GSP）拍卖并做进一步设计。我们设计的背后思想是利用个性化排名分数作为分配物品的标准，并基于预算计算关键ROI，以将预算的约束转化为与ROI相同的维度。

本文工作已被IJCAI-2023接收，欢迎阅读交流。

论文：Truthful Auctions for Automated Bidding in Online Advertising

下载：https://arxiv.org/abs/2301.13020

作者：Yidan Xing, Zhilin Zhang, Zhenzhe Zheng, Chuan Yu, Jian Xu, Fan Wu, Guihai Chen

1. 背景

随着机器学习在在线广告领域取得的成功，广告主们开始转向采用自动出价工具，这为广告主和在线平台之间的互动带来了重大变革。在自动出价服务中，广告主向平台提交其高层次的优化目标和约束条件，然后由机器学习算法驱动的出价代理代表广告主在每次广告拍卖中做出详细的出价决策。通过自动出价工具，广告主能够从全局角度针对其经济约束优化其整体广告目标。在自动出价下，我们需要重新审视拍卖理论中的一个基本问题：在自动出价的新广告范式中，传统的拍卖模型是否仍然适用。由于平台可以获取有关广告主与用户之间互动的历史数据，我们可以估计用户的潜在行为（如点击和转化），这些行为可以被视为广告主对物品的估值。在自动出价中，广告主的私有信息实际上是其在整个广告投放过程的约束条件。这些与传统拍卖截然不同的新特点需要对应的新广告拍卖模型，以激励广告主真实地揭示其高层次的私有约束。

在这项工作中，我们考虑了一种新的自动出价拍卖模型，在这个模型中，广告主提交预算以及投资回报率（ROI）要求作为他们的私有约束，并希望在一定时期的多次拍卖中最大化其赢得流量的累积价值。我们分析了与预算和投资回报率这两个私有约束相关的激励兼容条件。我们证明了，针对这种多维设定的任何可行（激励兼容且个体理性）的拍卖机制都可以等效地表示为一系列以预算为输入的非递减函数。当这些非递减函数被映射为相应的拍卖机制时，呈现出一种新的价值分组现象：不同的预算-投资回报率类型被分组以共享相同的累积价值，并且分组模式由一个阈值投资回报率函数（从上述非递减函数转换而来）以及它的单调性确定。由于阈值投资回报率函数可以拥有任意的单调性，预算-投资回报率类型的分组形状通常是不规则的，因此我们难以获得拍卖优化目标（如收入和社会福利）的闭式表达式。

为了克服这些困难而设计出易于实现的拍卖，我们提出了一系列允许个性化排名分数的广告拍卖，这个框架可以提供优化各种设计目标的灵活性。我们的拍卖机制采用排名分数作为分配的依据，与广义第二价格（GSP）拍卖的思想相似。为了保证私有约束的真实上报，我们设计了一类关键ROI，其定义为在不违反预算约束的情况下赢得最多物品的最大ROI，从而等效地将预算转化为与ROI相同的维度，使我们能够在预算和ROI间找到相对更严格的约束，并利用这个约束防止虚报。

2. 拍卖模型

基于上述的自动出价广告系统，我们考虑如下的拍卖模型。有$n$个广告主竞争$m$个物品（用户流量），这些物品在一个时间段内按顺序出现在$m$个时间段中，每个时间段只会出现一个物品。在整个工作中，我们将广告主和竞拍者、物品和用户流量视为等价的术语。这些广告主是“价值最大化”的竞拍者，在经济约束没有被违反的前提下，他们的目标是最大化在所有时间段内分配到的物品的累积价值。每个广告主$i$都有预算（$B_i\ge 0$）和投资回报率（ROI）（$R_i>0$）的约束，这些是私人信息，也可以称为类型 $t_i=(B_i,R_i)$。我们用$\mathbf{t}=(t_i{)}_{i=1}^n$ 表示所有广告主的类型，其空间为 $\mathcal{T}={\prod }_{i=1}^n{\mathcal{T}}_i$，其中$\mathbf{t}\in \mathcal{T}$且 ${\mathcal{T}}_i={\mathcal{B}}_i\times {\mathcal{R}}_i$。我们用${\mathbf{t}}_{-i}=(t_1,\dots ,t_{i-1},t_{i+1},\dots ,t_n)$和${\mathcal{T}}_{-i}={\prod }_{k\ne i}^n{\mathcal{T}}_k$表示广告主$i$之外的其他竞拍者的类型。我们假设广告主对物品的估值是平台已知的公共信息，并用$v_{i,j}>0$来表示广告主$i$对物品$j$的估值。

在收集了所有竞拍者的预算和ROI之后，在线平台采用某个拍卖机制 $(\mathcal{A},\mathcal{P})$ 来决定广告分配和支付，其中 $\mathcal{A}$ 表示一个（随机化的）分配规则$\mathcal{A}:\mathcal{T}\to [0,1{]}^{n\times m}$，而 $\mathcal{P}$ 表示一个（随机化的）支付规则 $\mathcal{P}:\mathcal{T}\to {\mathbb{R}}^n$。具体来说，如果平台收集到的上报类型是 ${\mathbf{t}}^{\prime }\in \mathcal{T}$，我们令竞拍者 $i$ 被分配到物品 $j$ 的概率表示为 $a_{i,j}({\mathbf{t}}^{\prime })$ ，而竞拍者 $i$ 的预期支付表示为 $p_i({\mathbf{t}}^{\prime })$ 。对于任何物品 $j\in [m]$，其必须满足的分配约束为  ${\sum }_{i=1}^n{a}_{i,j}({\mathbf{t}}^{\prime })\le 1$。竞拍者 $i$ 在这些拍卖中的累积价值可以由此表示为$v_i({\mathbf{t}}^{\prime })={\sum }_{j=1}^m{v}_{i,j}{a}_{i,j}({\mathbf{t}}^{\prime })$，她的实际投资回报率则可以被计算为${\mathrm{ROI}}_i({\mathbf{t}}^{\prime }):=v_i({\mathbf{t}}^{\prime })/p_i({\mathbf{t}}^{\prime })$（如果 $p_i({\mathbf{t}}^{\prime })=0$，将其视为 $+\infty$）。

当竞拍者的真实类型为 $t_i=(B_i,R_i)$ 时，上报类型 $t_i^{\prime }$ 时的效用被定义为：

$$u_i\left(t_i,{\mathbf{t}}^{\prime }\right)=\{\begin{array}{rl}{v}_i({\mathbf{t}}^{\prime }),& \text{ if }{p}_i({\mathbf{t}}^{\prime })\le B_i\text{ and }{\mathrm{ROI}}_i({\mathbf{t}}^{\prime })\ge R_i,\\ -\infty ,& \text{ otherwise, }\end{array}$$

其中${\mathbf{t}}^{\prime }=(t_i^{\prime },{\mathbf{t}}_{-i}^{\prime })$。

在这项工作中，我们专注于设计满足预算和投资回报率的占有策略激励兼容（DSIC）和个体理性（IR）性质的直接显示（direct-revelation）拍卖机制。

定义1：如果拍卖机制满足以下条件，则称该拍卖机制是满足占有策略激励兼容（DSIC）性质的： $\forall i\in [n]$, $t_i,t_i^{\prime }\in {\mathcal{T}}_i,{\mathbf{t}}_{-i}\in {\mathcal{T}}_{-i}$: $u_i(t_i,(t_i,{\mathbf{t}}_{-i}))\ge u_i(t_i,(t_i^{\prime },{\mathbf{t}}_{-i}))$.

定义2：如果拍卖机制满足以下条件，则称该拍卖机制是满足个体理性（IR）性质的：$\forall \mathbf{t}\in \mathcal{T}$, $i\in [n]$: $p_i(\mathbf{t})\le B_i$ 且 ${\mathrm{ROI}}_i(\mathbf{t})\ge R_i$.

当竞拍者拥有经济约束时，我们用流动福利(liquid welfare)来替代传统的社会福利，用于衡量所有主体在拍卖中的总收益：

$$\mathrm{LW}=\sum _{i\in [n],u_i(t_i,{\mathbf{t}}^{\prime })\ge 0}\min \left(\frac{v_i({\mathbf{t}}^{\prime })}{R_i},B_i\right).$$

3. 机制设计的可行域

在这一节中，我们将推导机制设计的可行域，即符合占有策略激励兼容（DSIC）和个体理性（IR）性质的机制的设计范围。由于篇幅限制，我们会省略部分推导的步骤与证明细节，呈现主要定理，感兴趣的读者朋友可查阅原论文。

为了使拍卖中私有约束和私有价值之间的区别更加直观，我们考虑只有一个私有约束（预算）的情况，并固定另一个约束（ROI）为真实值。为了使竞拍者真实地上报预算，我们需要确保竞拍者不会通过报告更小或更大的预算来获得更高的效用。因为报告更小的预算不会导致竞拍者打破她原有的预算约束，因此减少预算应当导致获得的效用等于或小于原先的效用。对于报告更大预算且获得更高价值的竞拍者，平台需要对其进行收费并打破原有的预算约束以防止虚报。

引理3：只有当拍卖机制满足以下性质时，该拍卖机制在预算上满足占有策略激励兼容（DSIC）性质：$\forall i\in [n]$, $R\in {\mathcal{R}}_i$, ${\mathbf{t}}_{-i}\in {\mathcal{T}}_{-i}$: (1) $v_i\left((B,R),{\mathbf{t}}_{-i}\right)$ 在$B$上单调递增; (2) 若$v_i\left((B^{\prime },R),{\mathbf{t}}_{-i}\right)>v_i\left((B,R),{\mathbf{t}}_{-i}\right)$ 对于某些 $B^{\prime }>B$成立, 那么  $p_i\left((B^{\prime },R),{\mathbf{t}}_{-i}\right)>B.$

对应地，我们可以写出当只有ROI是私有约束时的DSIC条件。

引理4：只有当拍卖机制满足以下性质时，该拍卖机制在投资回报比上满足占有策略激励兼容（DSIC）性质：$\forall i\in [n]$, $B\in {\mathcal{B}}_i$, ${\mathbf{t}}_{-i}\in {\mathcal{T}}_{-i}$: (1) $v_i\left((B,R),\right){\mathbf{t}}_{-i}$ 在$R$上单调递减；(2) 若$v_i\left((B,R^{\prime }),{\mathbf{t}}_{-i}\right)>v_i\left((B,R),{\mathbf{t}}_{-i}\right)$，对于某些 $R’<R $ 成立, 那么 $ ROI_i\left((B, R’), \boldsymbol{t}_{-i}\right)<R$. 。

上述引理中的单调递增/递减是非严格的。引理3与引理4自然地构成了$(B,R)$双参数DSIC的必要条件。我们进一步证明了，它们实际上也构成了充要条件，也就是说，当竞拍者无法通过在单参数上的虚报获得更高效益时，也同样无法通过双参数上的同时虚报来获得更高的效益。

定理5：拍卖机制满足引理3与引理4是占有策略激励兼容（DSIC）性质的充要条件。

接下来，我们想要在机制设计时对分配和支付规则进行分解。我们找到了一个“万能”的支付规则，满足如下性质：只要对于特定的分配规则，存在某个支付规则使得拍卖机制是DSIC与IR的，那么该支付规则就一定可以使其与分配规则组成的拍卖机制保持DSIC与IR。该支付规则在给定的分配与约束下，收取最大的可能支付，其具体形式是：

$$p_i\left((B_i,R_i),{\mathbf{t}}_{-i}\right)=\min \left(v_i\left((B_i,R_i),{\mathbf{t}}_{-i}\right)/R_i,B_i\right)$$

然后，将其重新代入定理5中，我们发现类型的累积价值与其预算乘以ROI的乘积之间的关系严格限制了其相邻类型的累积价值（定理6）。

定理6：分配规则可以与某个支付规则组成DSIC和IR的拍卖机制，当且仅当其满足如下条件：$\forall \mathbf{t}\in \mathcal{T}$, $i\in [n]$:
（1）$v_i\left((B,R),{\mathbf{t}}_{-i}\right)$ 在 $B$ 上单调递增，在 $R$ 上单调递减；（2）若 $v_i\left((B_i,R_i),{\mathbf{t}}_{-i}\right)>{\lim }_{B\to B_i^{-}}{v}_i\left((B,R_i),{\mathbf{t}}_{-i}\right)$, 那么 $v_i\left((B_i,R_i),{\mathbf{t}}_{-i}\right)\ge B_i\times R_i$；（3）若 $v_i\left((B_i,R_i),{\mathbf{t}}_{-i}\right)>{\lim }_{R\to R_i^{+}}{v}_i\left((B_i,R),{\mathbf{t}}_{-i}\right)$，那么 $v_i\left((B_i,R_i),{\mathbf{t}}_{-i}\right)\le B_i\times R_i$。

在定理6中，一个重要的观察是，对于每个预算，必定存在一个阈值ROI，在此之后，即使上报的ROI要求降低，分配的累计价值也不会再增加，其定义如下：

$${\mathrm{thr}}_i(B,{\mathbf{t}}_{-i})=\underset{R\in {\mathcal{R}}_i}{\sup }\left(v_i\left((B,R),{\mathbf{t}}_{-\mathbf{i}}\right)\ge B\times R\right)$$

定理7：$\forall i\in [n]$, ${\mathbf{t}}_{-i}\in {\mathcal{T}}_{-i}$, $B_i\in {\mathcal{B}}_i$, $R_i\le {\mathrm{thr}}_i(B_i,{\mathbf{t}}_{-i})$:  $v_i\left((B_i,R_i),\mathbf{t}-\mathbf{i}\right)={\mathrm{thr}}_i(B_i,{\mathbf{t}}_{-i})B_i.$

进一步，我们发现所有ROI高于其预算对应的阈值ROI的类型都必须与其同行相邻的类型（相同ROI，不同预算）具有相同的累积价值。

定理8：$\forall i\in [n]$, ${\mathbf{t}}_{-i}\in {\mathcal{T}}_{-i}$, B i ∈ B i \ { 0 } B_i\in \mathcal{B}_i\backslash\{0\} Bi​∈Bi​\{0}, $R_i>{\mathrm{thr}}_i(B_i,{\mathbf{t}}_{-i})$:  $v_i((B_i,R_i),{\mathbf{t}}_{-i})={\lim }_{B\to B_i^{-}}{v}_i\left((B,R_i),{\mathbf{t}}_{-i}\right).$

结合定理7与8，我们发现阈值ROI函数可以唯一定义相应的累积价值函数，只要预算乘以其阈值ROI是单调递增的，而且这个映射关系是双射的。为了方便表示，我们定义 $g_i(B_i,{\mathbf{t}}_{-i})={\mathrm{thr}}_i(B_i,{\mathbf{t}}_{-i})\times B_i$。我们将$\mathcal{V}$表示为在固定$i$和${\mathbf{t}}_{-i}$的情况下可行的累积价值函数（$v_i:T_i\to {\mathbb{R}}^{+}$）的空间，并将$\mathcal{G}$表示为非严格递增函数$g:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$且满足$g(0)=0$的空间。

定理9：存在一个双射的映射$m:\mathcal{G}\to \mathcal{V}$，其定义为：

其中我们假设$\sup \varnothing =0$。

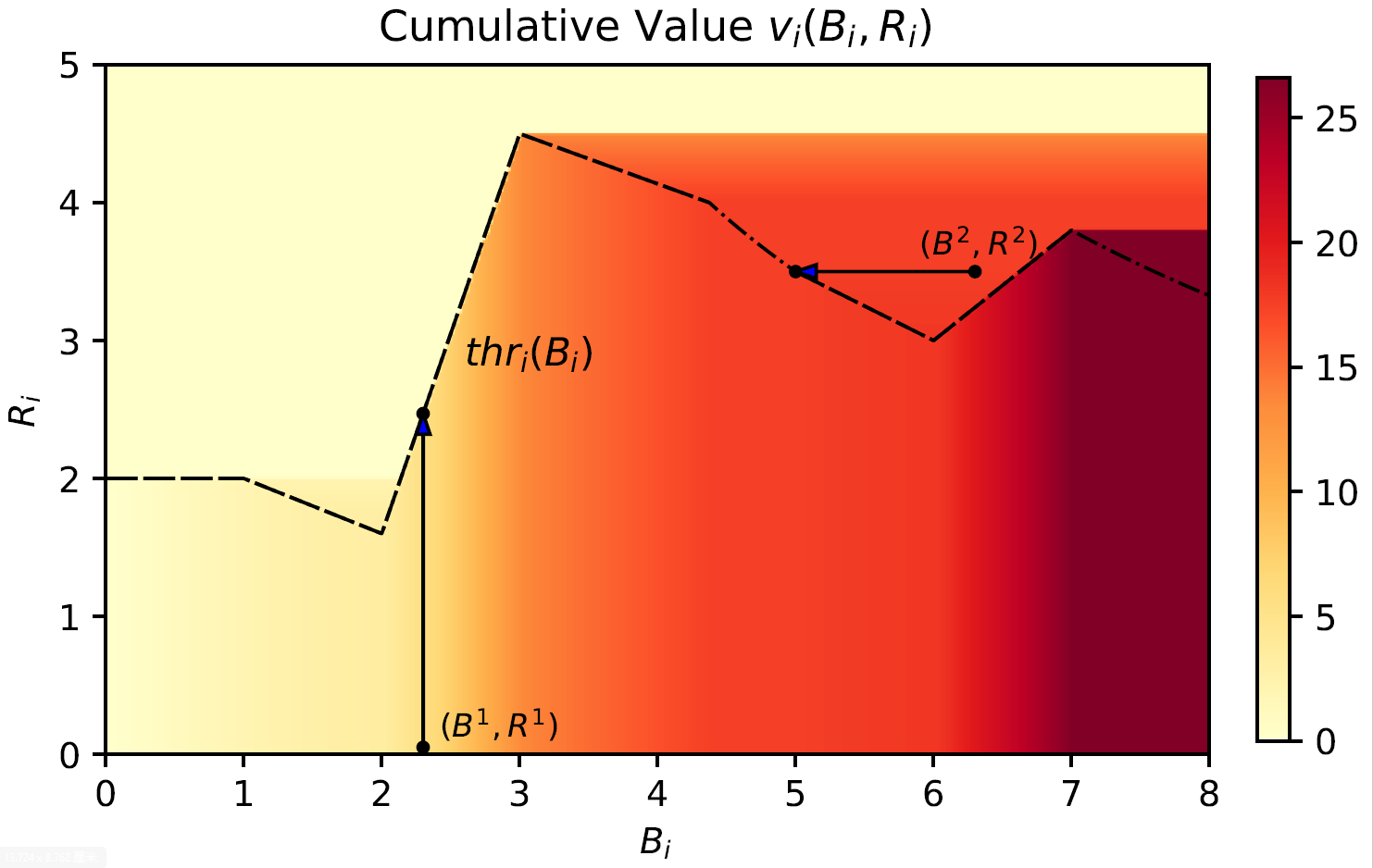
也就是说，给定阈值ROI函数后，每种类型都会通过在垂直或水平方向上与阈值ROI曲线相交来与某些类型共享相同的累积价值，且所有类型的累积价值都会以这种方式被确定。具体来说，阈值ROI曲线上的类型需要拥有与其自身$B\times R$相同的累计价值，阈值ROI曲线下方的类型会在垂直方向上向上搜索，而其上方的类型在水平方向上向左搜索，从而与阈值ROI曲线相交，并与该交点拥有相同的累积价值。我们可以通过设计阈值ROI函数来设计相应的拍卖机制，而每个满足DSIC与IR的拍卖机制也独特地对应一种阈值ROI函数。在这种结构下，由于阈值ROI曲线上方的类型通过在水平方向上向左搜索而与阈值ROI曲线相交，不同类型会根据阈值ROI函数的单调性而被分组，并拥有相同的累积价值，但是，由于阈值ROI函数本身可以拥有任意的单调性，在整个可行域中获得设计目标的通用表达式是困难的。

4. 基于排序函数的激励兼容机制设计

基于以上的机制设计可行域分析，我们提出了一类基于排序函数的激励兼容机制，其排序函数灵活可变，且机制易于实现。设计的关键思想是采用提前确定的排序函数为每个物品分别对广告主进行排名，并将阈值ROI设计为赢得足够多的物品以消耗完预算的最大ROI。这在我们的拍卖中被称为关键ROI，模拟了广告主在面对竞拍价格时的最优反应。该机制设计的具体流程如下：

在该机制中，给定广告主上报的预算和ROI，我们首先基于排序函数计算不同广告主对于每个物品的虚拟出价。只要这些排序函数在ROI上是单调递减的，我们就可以保证最终的拍卖机制是满足DSIC与IR的。接下来，我们将每个物品分配给排序分数最高的广告主，并根据第二高的排序函数计算她赢得此物品所需要的ROI。为了保证约束的真实上报，我们使用前面提到的基本规则来计算关键ROI，即赢得足够多的物品以消耗完预算的最大ROI，其中我们使用关键ROI作为实际ROI来计算支付。即使广告主的真实ROI低于此关键ROI，她最终的分配也会根据此关键ROI进行调整。最后，我们按照之前找到的“万能”支付规则进行扣费。这样的机制是IC的，从直觉上来说是因为我们根据关键ROI（代表了预算）和上报ROI中更紧的一项决定分配，如果广告主通过虚报而获得更好的分配，她就一定有至少一个真实的约束被违反了，反而会导致负效益。

5. 实验结果

我们在不同的自动出价环境中验证了所提出的拍卖机制的性能。在这里仅简要描述实验设定，完整的设定请参照原论文。为了模拟自动出价中广告主的不同类型与对物品的估值，我们令$v,B,R$从均匀分布中取值，并考虑如下的两种环境：(1) i.i.d.环境，即每位广告主的参数均从同样的均匀分布中取值；(2) non-i.i.d.环境，每位广告主的$v,B,R$可以从特定的高/低均匀分布中取值，共8种广告主。我们采用了重复一价和二价拍卖，以及基于线性规划的理论最优解作为基准，这三种基准拍卖都不满足DSIC性质。我们基于流动福利、拍卖收入和公平性对不同机制进行评估，公平性定义为$\mathrm{fairness}={\min }_{i\in [n]}\min \left(\frac{v_i({\mathbf{t}}^{\prime })}{R_i},B_i\right)$。我们将排序函数设计为$f_{i,j}(R)={\alpha }_{i,j}\times e^{-\beta R}$的形式，其中${\alpha }_{i,j}$从正态分布$N({\mu }_i,{\sigma }_i^2)$中采样，$\beta ,{\mu }_i,{\sigma }_i$是提前设置的常数，根据不同的实验环境选取这些参数。

实验的结果如下：

在i.i.d.环境中，可以观察到，相较于重复一价与二价拍卖，我们的方法在收入和流动福利方面表现更好，并且更接近于理论最优解（图3(a)与3(b)）。我们发现，为了实现更高的收入，不可避免地需要进行差别化的分配，而这种公平性和收入之间的权衡可以通过排序函数中的参数进行调整（图3©与3(d)）。

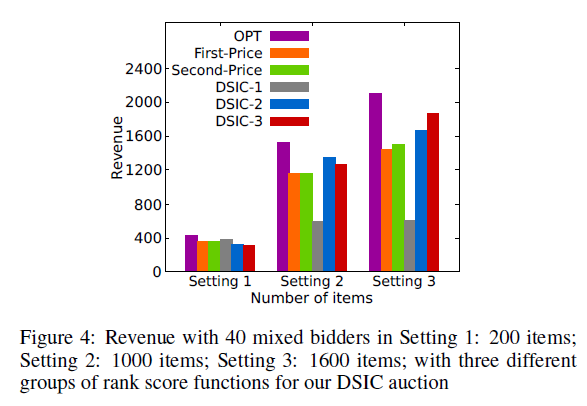
在non-i.i.d.环境中，我们不再呈现与i.i.d.环境中类似的趋势，而进一步说明选择适当的排名分数函数的重要性。我们选择了三组分别在各自对应得设定中性能良好的排序函数，并在其他两种设定中测试其性能。结果在图4中呈现，其中DSIC-$n$表示在第 $n$ 个设定中表现良好的真实拍卖。DSIC-$n$ 机制只在第 $n$ 个设定中表现良好，其原因可能来自于为了在不同数量的物品下实现高收入而需要不同的分配方法。例如，在物品短缺的情况下（设定1），DSIC-1 拍卖将大部分物品分配给$v$高、ROI低的竞标者，导致在设定2和3中向这些广告主分配过多的物品而导致浪费。

6. 结论

本文中，在自动出价场景下我们考虑了具有私有预算和投资回报率约束的广告主在多物品拍卖中的拍卖机制设计，其中物品的价值是公开的信息。我们刻画了这个新的自动出价拍卖模型中的DSIC和IR条件，其中涉及到使竞拍者不同类型共享累积效用的新颖分组约束。我们提出了一系列易于实现且可灵活调整的激励兼容拍卖机制，实验结果验证了所提出的拍卖机制的性能表现。

▐ 部分参考文献

[Edelman et al., 2007] Benjamin Edelman, Michael Ostrovsky, and Michael Schwarz. Internet advertising and the generalized second-price auction: Selling billions of dollars worth of keywords. American Economic Review, 97(1):242–259, March 2007.

[Aggarwal et al., 2019] Gagan Aggarwal, Ashwinkumar Badanidiyuru, and Aranyak Mehta. Autobidding with constraints. In International Conference on Web and Internet Economics, pages 17–30. Springer, 2019.

[Balseiro et al., 2021b] Santiago R Balseiro, Yuan Deng, Jieming Mao, Vahab S Mirrokni, and Song Zuo. The landscape of auto-bidding auctions: Value versus utility maximization. In Proceedings of the 22nd ACM Conference on Economics and Computation, pages 132–133, 2021.

[Balseiro et al., 2022] Santiago Balseiro, Yuan Deng, Jieming Mao, Vahab Mirrokni, and Song Zuo. Optimal mechanisms for value maximizers with budget constraints via target clipping. In Proceedings of the ACM Conference on Economics and Computation, page 475. ACM, 2023.