【Unity编程】欧拉角与万向节死锁（图文版）

万向节死锁（Gimbal Lock）问题

上文中曾经说过，欧拉旋转的顺规和轴向定义，自然造就了“万向节死锁”问题。本文主要来探索它自然形成的原因。

陀螺仪

首先，我们来了解Gimbal 究竟是个什么玩意儿。下面来自维基百科中关于Gimbal的一段引述：

---

平衡环架（英语：Gimbal）为一具有枢纽的装置，使得一物体能以单一轴旋转。由彼此垂直的枢纽轴所组成的一组三只平衡环架，则可使架在最内的环架的物体维持旋转轴不变，而应用在船上的陀螺仪、罗盘、饮料杯架等用途上，而不受船体因波浪上下震动、船身转向的影响。

---

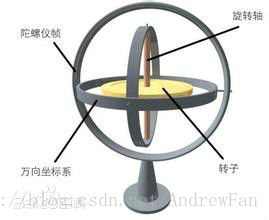
上图就是一个Gimbal装置了，它是一个陀螺仪。中间有一根竖轴，穿过一个金属圆盘。金属圆盘称为转子，竖轴称为旋转轴。转子用金属制成，应该是了增加质量，从而增大惯性。竖轴外侧是三层嵌套的圆环，它们互相交叉，带来了三个方向自由度的旋转。
看着不停转来转去，有点晕，接下来看两个静态的。这两张图来自百度百科。

中文注释：

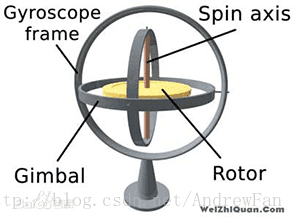
其中Gimbal只代表陀螺仪装置中的平衡环，显然维基百科上将它解释成“平衡环架”更为合理。

Pitch、Yaw、Roll

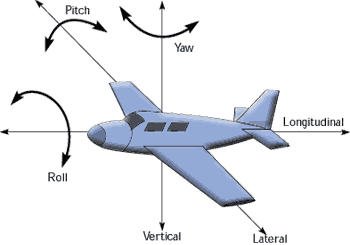
在解释陀螺仪的工作原理之前，我先介绍一些转动的术语。在飞行器的航行中，进行XYZ三个方向旋转的旋转有专业的术语，见下图：

沿着机身右方轴（Unity中的+X）进行旋转，称为pitch，中文叫俯仰。
沿着机头上方轴（Unity中的+Y）进行旋转，称为Yaw，中文叫偏航。
沿着机头前方轴（Unity中的+Z）进行旋转，称为Roll，中文叫桶滚。

陀螺仪的工作原理

我们知道陀螺仪使用来测量平衡和转速的工具，在载体高速转动的时候，陀螺仪始终要通过自我调节，使得转子保持原有的平衡，这一点是如何做到的？带着这个问题，我们来看一下这个古老而又神秘的装置的工作原理。

为了解释清楚问题，我自己画了一个简单的陀螺仪示意图。（金属圆盘我就省略了，丑点儿也就别管了。。）

这里，我把三个Gimbal环用不同的颜色做了标记，底部三个轴向，RGB分别对应XYZ。
假设现在这个陀螺仪被放在一艘船上，船头的方向沿着+Z轴，也就是右前方。

• 现在假设，船体发生了摇晃，是沿着前方进行旋转的摇晃，也就是桶滚。由于转子和旋转轴具有较大的惯性，只要没有直接施加扭矩，就会保持原有的姿态。由于上图中绿色的活动的连接头处是可以灵活转动的，此时将发生相对旋转，从而出现以下的情形：
  

• 再次假设，船体发生了pitch摇晃，也就是俯仰。同样，由于存在相应方向的可以相对旋转的连接头（红色连接头），转子和旋转轴将仍然保持平衡，如下图：
  

• 最后假设，船体发生了yaw摇晃，也就是偏航，此时船体在发生水平旋转。相对旋转发生在蓝色连接头。如下图：
  

最终，在船体发生Pitch、Yaw、Roll的情况下，陀螺仪都可以通过自身的调节，而让转子和旋转轴保持平衡。

陀螺仪中的万向节死锁

现在看起来，这个陀螺仪一切正常，在船体发生任意方向摇晃都可以通过自身调节来应对。然而，真的是这样吗？

假如，船体发生了剧烈的变化，此时船首仰起了90度（这是要翻船的节奏。。。。），此时的陀螺仪调节状态如下图：

此时，船体再次发生转动，沿着当前世界坐标的+Z轴（蓝色轴，应该正指向船底）进行转动，那么来看看发生了什么情况。

现在，转子不平衡了，陀螺仪的三板斧不起作用了。它失去了自身的调节能力。那么这是为什么呢？
之前陀螺仪之所以能通过自身调节，保持平衡，是因为存在可以相对旋转的连接头。在这种情况下，已经不存在可以相对旋转的连接头了。
那么连接头呢？去了哪里？显然，它还是在那里，只不过是，连接头可以旋转的相对方向不是现在需要的按着+Z轴方向。从上图中，我们清楚地看到：

• 红色连接头：可以给予一个相对俯仰的自由度。
• 绿色连接头：可以给予一个相对偏航的自由度。
• 蓝色连接头：可以给予一个相对偏航的自由度。

没错，三个连接头，提供的自由度只对应了俯仰和偏航两个自由度，桶滚自由度丢失了。这就是陀螺仪上的“万向节死锁”问题。

用小程序来重现万向节死锁问题

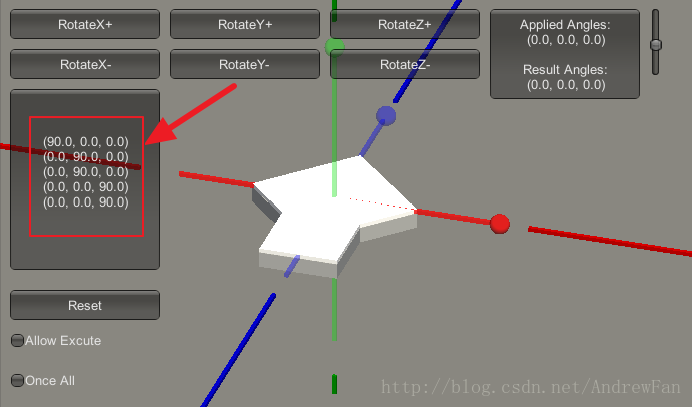
首先，预设一下接下来的欧拉角变化顺序。见下图：

上图中，红色框内的部分的列表，记录了接下来欧拉角的增长变化过程。即它会从(0,0,0)变化到(90,0,0)，再变化到(90,90,0)，再变化到(90,180,0)，再变化到(90,180,90)，再变化到(90,180,180)。下图是变化的过程演示。

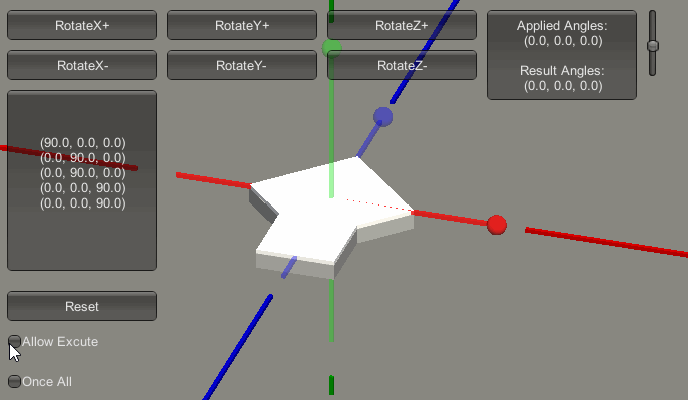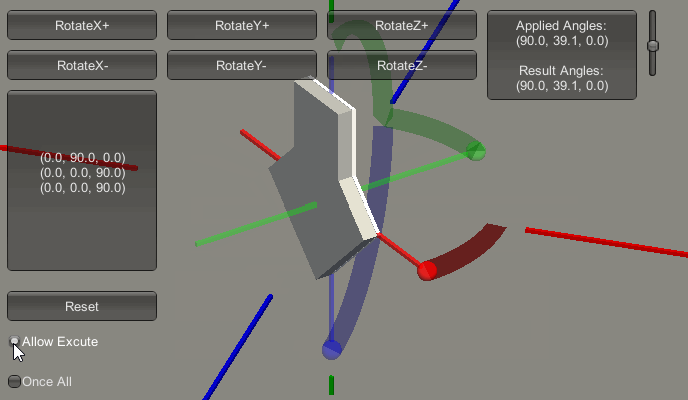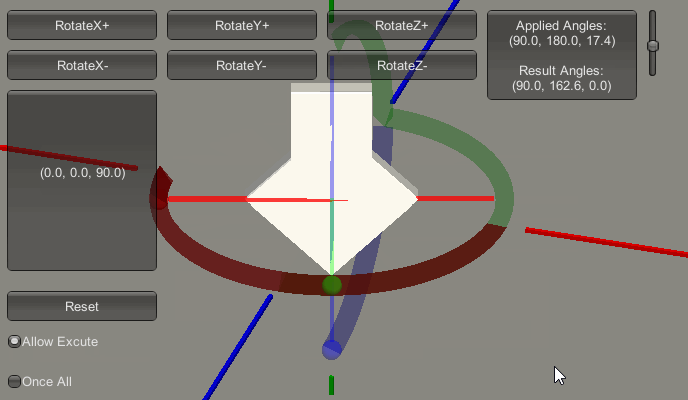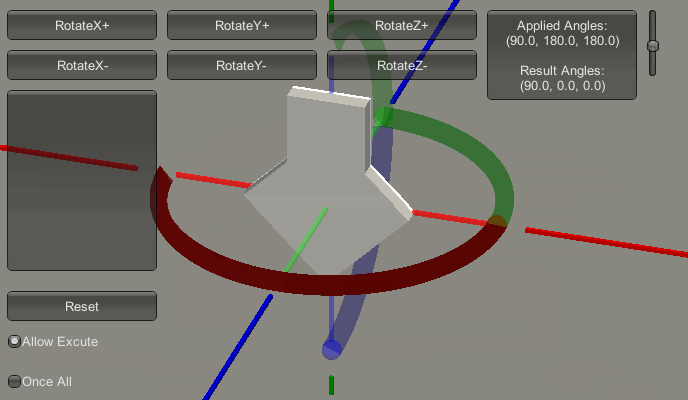
现在可以看到：
- 当先执行X轴旋转90度，此时在执行Pitch(俯仰)变化。
- 再在Y轴进行变化0-180度，此时在执行相对自身的Roll(桶滚)变化。
- 再在Z轴进行变化0-180度，此时仍在执行相对自身的Roll(桶滚)变化。

这里所说的俯仰、桶滚、偏航都是相对自己局部坐标系的。这与上述的陀螺仪中出现的问题是一样的，万向节死锁。也就是尽管欧拉角在XYZ三个轴向进行进动(持续增长或者减少)，但是影响最终的结果，只对应了两个轴向。

死锁的过程解析

在《Unity中欧拉旋转》一文中我曾提到，是欧拉角顺规和轴向的定义方式，造就了“万向节死锁”问题的自然形成。通过上述的例子，这里作个详细解释。

首先我们知道，由于Unity中欧拉旋转的顺规的定义，围绕Z轴的进动最先执行，所以，Z轴是“严格保护”的一个轴，就是说，当先沿着Z轴进行进动时，无论此时的XY是什么值，最终的结果，围绕Z轴的进动始终造成相对自身执行桶滚变化。
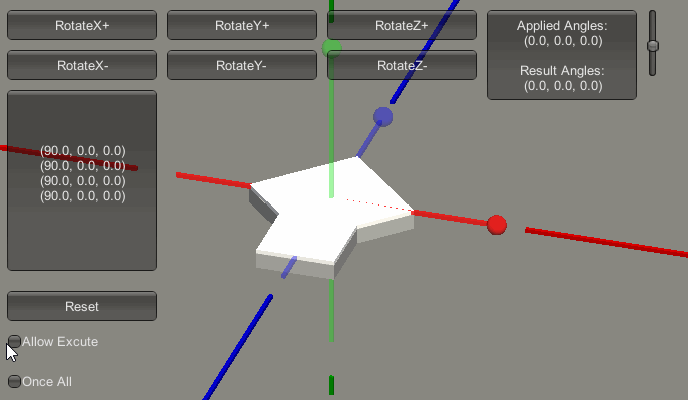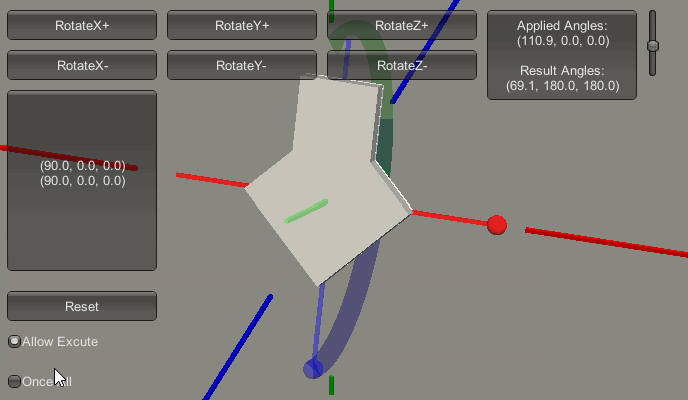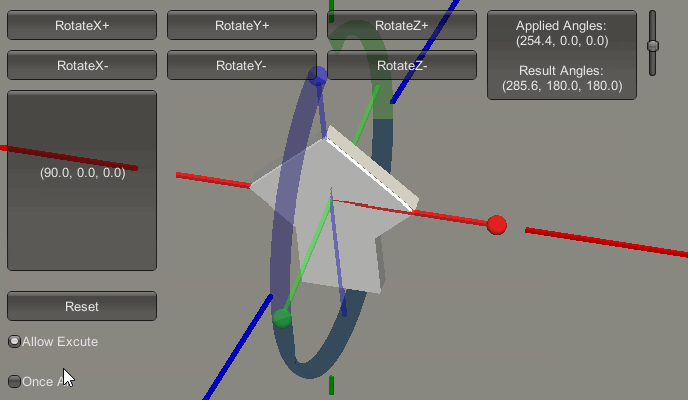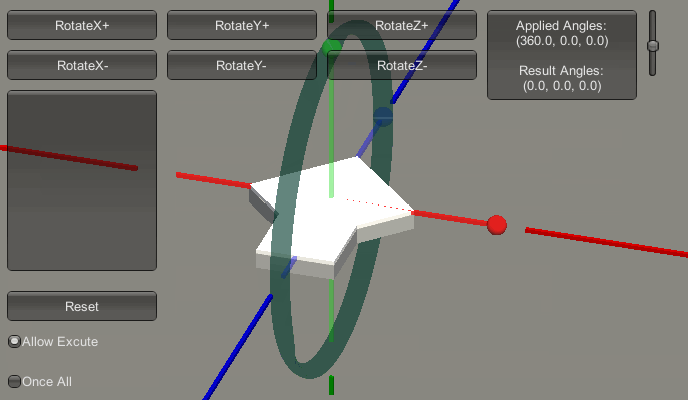
然而X、Y轴就不同了，我们先不考虑Y轴，假设其一直为0，先说X轴。如果Z轴也是保持为0，那么围绕X轴进动，最终的影响是预期的俯仰变化。如下图：

然而当Z轴为90度时，围绕X轴进动变成了偏航变化，如下图：

也就是说，欧拉角的X轴进动造成最后的变化结果，受到到了预先执行的Z轴进动的影响，它仍然会造成某个相对自身的轴向的变化，但是结果不唯一；同样，欧拉角的Y轴进动，则受到了Z轴和X轴的影响，结果更加不唯一。

然而，以上的过程执行，都是严格遵守欧拉角的顺规和轴向定义的。某些时刻，这种不确定的结果，就可能造成某个轴向自由度的丢失。
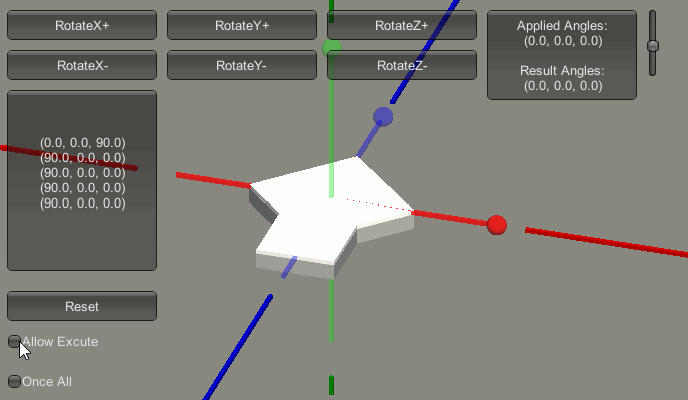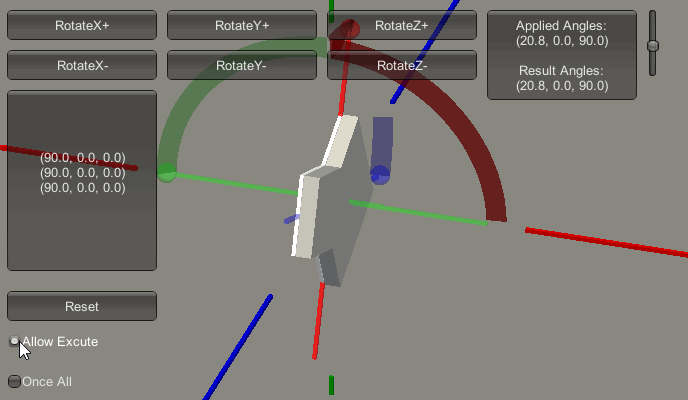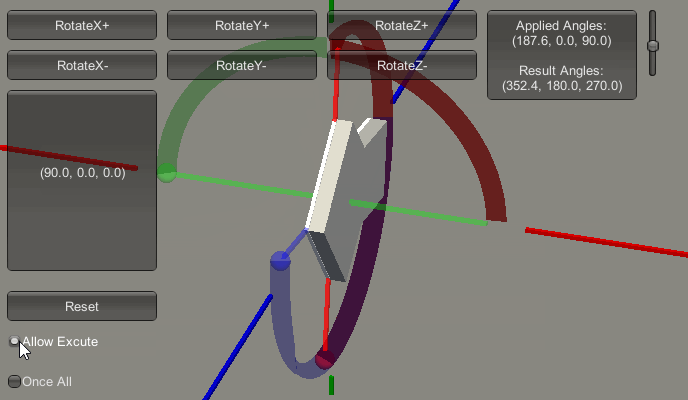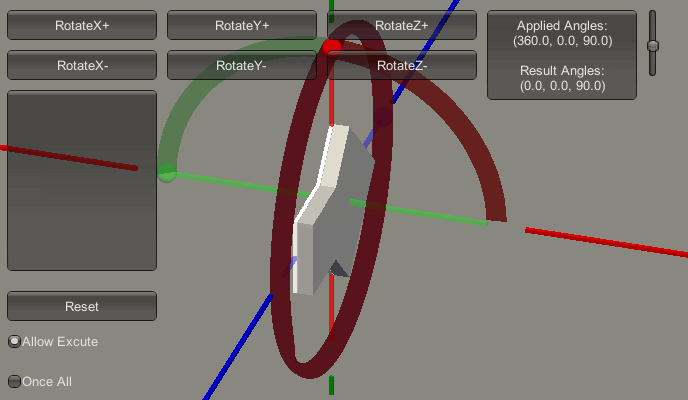
就拿下图来说：

欧拉角Z轴的进动，最先执行，造成桶滚，这个没问题。
欧拉角Y轴的进动，最后执行，造成沿着欧拉旋转前的Y轴旋转，这也是根据定义执行。然而现在这种沿着Y轴的旋转，同样也被映射到了物体的桶滚变化。

总结

总结来说，欧拉角的“万向节死锁”问题，是由于欧拉旋转定义本身造成的。这种围绕选旋转前固定轴的先Z、再X、再Y的旋转操作，与其最终所预期的三个轴向可以旋转的结果并非一定是一对一的映射。某些情况下是多对一的映射，造成一些旋转自由度的缺失，也就是“死锁”。

建议

对于写代码来说，你直接去改变Transform的欧拉角显然是不合适的，通过本文也可以看到，这种结果几乎是不可预测的。但是某些情况下，却是可以预期的，就是你仅仅在一个轴向进动，其它两个轴向保持为0，此时有效，并且直接修改欧拉角的代码效率应该是比较高的。