PID调节的C语言及MATLAB实现方法

最新推荐文章于 2024-04-29 11:12:48 发布

unique_jie

最新推荐文章于 2024-04-29 11:12:48 发布

阅读量2k

点赞数

分类专栏：嵌入式C语言文章标签： matlab c语言 pid

本文链接：https://blog.csdn.net/aoyousihaiqiuqihuang/article/details/119980723

版权

嵌入式C语言专栏收录该内容

16 篇文章 14 订阅

订阅专栏

在模拟控制系统中，控制器最常用的控制规律就是PID控制，控制系统的原理框图如图所示：

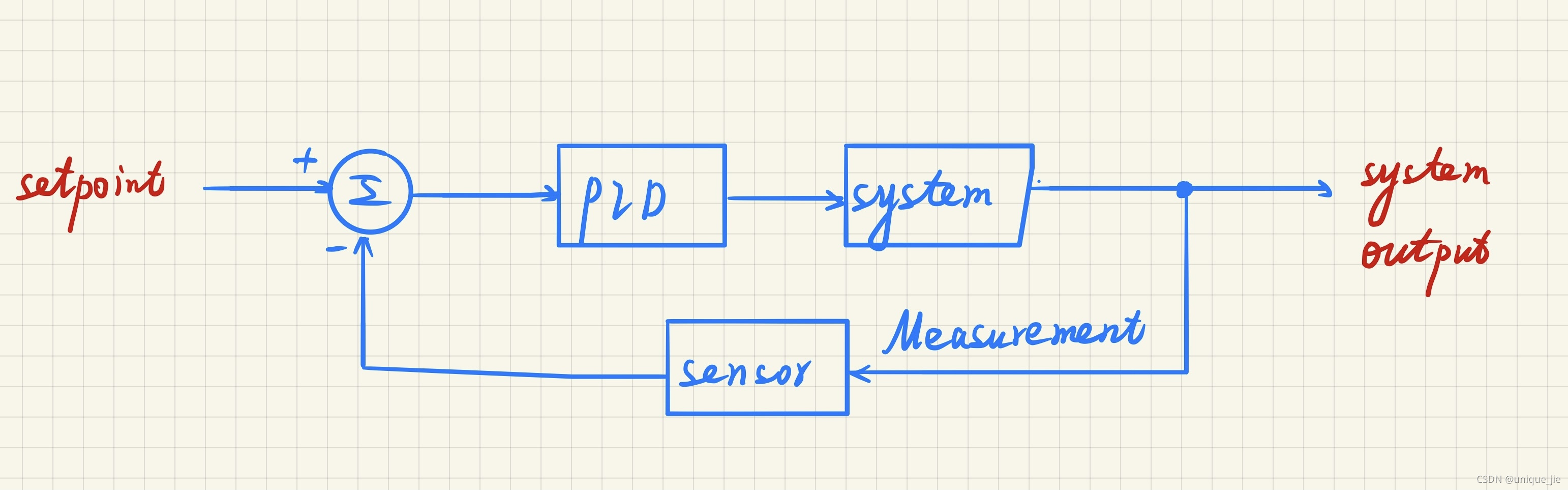
在实现PID控制的过程中，关键的部分除了PID三个参数之外，就是system和系统反馈了，需要能够拿到系统当前的输出，才能够形成一个闭环的反馈控制系统，而system就是系统本身的特性，表征系统自身的输入与输出之间的关系，从而能够将PID控制器的输出叠加到系统输出上。将连续系统进行离散化处理，就能得到PID在离散系统中的表达。

C语言中构建PID控制器如下：

typedef struct {
	/* Controller gains */
	float Kp;
	float Ki;
	float Kd;
	/* Output limits */
	float limMin;
	float limMax;
	/* Integrator limits */
	float limMinInt;
	float limMaxInt;
	/* Sample time (in seconds) */
	float T;
	/* Controller "memory" */
	float integrator;
	float prevError;			/* Required for integrator */
	float differentiator;
	float prevMeasurement;		/* Required for differentiator */
	/* Controller output */
	float out;
} PIDController;

初始化PID控制器：

void PIDController_Init(PIDController *pid) {

	/* Clear controller variables */
	pid->integrator = 0.0f;
	pid->prevError  = 0.0f;

	pid->differentiator  = 0.0f;
	pid->prevMeasurement = 0.0f;

	pid->out = 0.0f;
}

控制方法的实现：


float PIDController_Update(PIDController *pid, float setpoint, float measurement) {

	/*Error signal*/
    float error = setpoint - measurement;

	/*Integral*/
	pid->integrator = pid->integrator + 0.5f *(error + pid->prevError);

	/* Anti-wind-up via integrator clamping */
    if (pid->integrator > pid->limMaxInt) {

        pid->integrator = pid->limMaxInt;

    } else if (pid->integrator < pid->limMinInt) {

        pid->integrator = pid->limMinInt;

    }

	/* Derivative (band-limited differentiator)*/
	pid->differentiator = (error - pid->prevError);	/* Note: derivative on measurement, therefore minus sign in front of equation! */

	/*Compute output and apply limits*/
    pid->out = (pid->Kp) * error + (pid->Ki)* (pid->integrator) + (pid->Kd) * (pid->differentiator);

    if (pid->out > pid->limMax) {

        pid->out = pid->limMax;

    } else if (pid->out < pid->limMin) {

        pid->out = pid->limMin;

    }

	/* Store error and measurement for later use */
    pid->prevError       = error;
    pid->prevMeasurement = measurement;

	/* Return controller output */
    return pid->out;
}

一个简单的测试demo：

#define PID_KP  0.9f
#define PID_KI  0.5f
#define PID_KD  0.0f

#define PID_LIM_MIN -10.0f
#define PID_LIM_MAX  10.0f

#define PID_LIM_MIN_INT -5.0f
#define PID_LIM_MAX_INT  5.0f

#define SAMPLE_TIME_S 0.1f

/* Maximum runtime of simulation */
#define SIMULATION_TIME_MAX 50.0f

/* Simulated dynamical system (first order) */
float TestSystem_Update(float inp);

int main()
{
    /* Initialise PID controller */
    PIDController pid = { PID_KP, PID_KI, PID_KD,
                          PID_LIM_MIN, PID_LIM_MAX,
			  PID_LIM_MIN_INT, PID_LIM_MAX_INT,
                          SAMPLE_TIME_S };

    PIDController_Init(&pid);

    /* Simulate response using test system */
    float setpoint = 2.0f;

    printf("Time (s)\tsetpoint\tsystem output\r\n");
    for (float t = 0.0f; t <= SIMULATION_TIME_MAX; t += SAMPLE_TIME_S) {

        /* Get measurement from system */
        float measurement = TestSystem_Update(pid.out);

        /* Compute new control signal */
        PIDController_Update(&pid, setpoint, measurement);

        printf("%f\t%f\t%f\r\n", t, setpoint, measurement);

    }
    return 0;
}

float TestSystem_Update(float inp) {

    float output;
     output = (1.0f + inp);
    return output;
}

测试结果如下：

Time (s)        setpoint        system output
0.000000        2.000000        1.000000
0.100000        2.000000        2.150000
0.200000        2.000000        1.327500
0.300000        2.000000        2.198375
0.400000        2.000000        1.533118
0.500000        2.000000        2.198976
0.600000        2.000000        1.666681
0.700000        2.000000        2.179332
0.800000        2.000000        1.756443
0.900000        2.000000        2.153100
1.000000        2.000000        1.818723
1.100000        2.000000        2.126706
1.200000        2.000000        1.863164
1.300000        2.000000        2.102885
1.400000        2.000000        1.895624
1.500000        2.000000        2.082531
1.600000        2.000000        1.919776
1.700000        2.000000        2.065679
1.800000        2.000000        1.938002
1.900000        2.000000        2.051991
2.000000        2.000000        1.951903
2.100000        2.000000        2.041009
2.200000        2.000000        1.962585
2.300000        2.000000        2.032268
2.400000        2.000000        1.970840
2.500000        2.000000        2.025348
2.600000        2.000000        1.977244
2.700000        2.000000        2.019890
2.799999        2.000000        1.982225
2.899999        2.000000        2.015594
2.999999        2.000000        1.986107
3.099999        2.000000        2.012220
3.199999        2.000000        1.989137
3.299999        2.000000        2.009573
3.399999        2.000000        1.991503
3.499999        2.000000        2.007497
3.599999        2.000000        1.993352
3.699999        2.000000        2.005870
3.799999        2.000000        1.994798
3.899998        2.000000        2.004596
3.999998        2.000000        1.995930
4.099998        2.000000        2.003598
4.199998        2.000000        1.996815
4.299998        2.000000        2.002816
4.399998        2.000000        1.997507
4.499998        2.000000        2.002204
4.599998        2.000000        1.998049
4.699998        2.000000        2.001726
4.799998        2.000000        1.998473
4.899998        2.000000        2.001351
4.999998        2.000000        1.998805
5.099998        2.000000        2.001057
5.199997        2.000000        1.999065
5.299997        2.000000        2.000827
5.399997        2.000000        1.999268
5.499997        2.000000        2.000648
5.599997        2.000000        1.999427
5.699997        2.000000        2.000507
5.799997        2.000000        1.999552
5.899997        2.000000        2.000397
5.999997        2.000000        1.999649
6.099997        2.000000        2.000310
6.199996        2.000000        1.999725
6.299996        2.000000        2.000243
6.399996        2.000000        1.999785
6.499996        2.000000        2.000190
6.599996        2.000000        1.999832
6.699996        2.000000        2.000149
6.799996        2.000000        1.999868
6.899996        2.000000        2.000116
6.999996        2.000000        1.999897
7.099996        2.000000        2.000091
7.199996        2.000000        1.999919
7.299995        2.000000        2.000071
7.399995        2.000000        1.999937
7.499995        2.000000        2.000056
7.599995        2.000000        1.999951
7.699995        2.000000        2.000044
7.799995        2.000000        1.999961
7.899995        2.000000        2.000034
7.999995        2.000000        1.999970
8.099995        2.000000        2.000027
8.199995        2.000000        1.999976
8.299995        2.000000        2.000021
8.399996        2.000000        1.999981
8.499996        2.000000        2.000016
8.599997        2.000000        1.999986
8.699997        2.000000        2.000013
8.799997        2.000000        1.999989
8.899998        2.000000        2.000010
8.999998        2.000000        1.999991
9.099998        2.000000        2.000008
9.199999        2.000000        1.999993
9.299999        2.000000        2.000006
9.400000        2.000000        1.999995
9.500000        2.000000        2.000005
9.600000        2.000000        1.999996
9.700001        2.000000        2.000004
9.800001        2.000000        1.999997
9.900002        2.000000        2.000003
10.000002       2.000000        1.999998
10.100002       2.000000        2.000002
10.200003       2.000000        1.999998
10.300003       2.000000        2.000002
10.400003       2.000000        1.999999
10.500004       2.000000        2.000001
10.600004       2.000000        1.999999
10.700005       2.000000        2.000001
10.800005       2.000000        1.999999
10.900005       2.000000        2.000001
11.000006       2.000000        1.999999
11.100006       2.000000        2.000000
11.200006       2.000000        2.000000
11.300007       2.000000        2.000000
11.400007       2.000000        2.000000
11.500008       2.000000        2.000000
11.600008       2.000000        2.000000
11.700008       2.000000        2.000000
11.800009       2.000000        2.000000
11.900009       2.000000        2.000000
12.000010       2.000000        2.000000
12.100010       2.000000        2.000000
12.200010       2.000000        2.000000
12.300011       2.000000        2.000000
12.400011       2.000000        2.000000

经过一段时间后，系统达到了理想的输出。接下来，在matlab中建立上面的模型：

给定了一个较大的微分系数，系统在经过了一段时间的振荡之后到达了稳定

同样的条件下，去掉微分项，结果如下：

本文中，系统输出与PID控制器输出是一个非常简单的线性关系，在PID控制的实际应用中通常需要系统特性的一个数学表达，将PID的输出叠加到系统输出中。

reference：

https://github.com/pms67/PID

unique_jie

关注

0
点赞
踩
21

收藏

觉得还不错? 一键收藏
0
评论
PID调节的C语言及MATLAB实现方法

在模拟控制系统中，控制器最常用的控制规律就是PID控制，控制系统的原理框图如图所示：在实现PID控制的过程中，关键的部分除了PID三个参数之外，就是system和系统反馈了，需要能够拿到系统当前的输出，才能够形成一个闭环的反馈控制系统，而system就是系统本身的特性，表征系统自身的输入与输出之间的关系，从而能够将PID控制器的输出叠加到系统输出上。将连续系统进行离散化处理，就能得到PID在离散系统中的表达。C语言中构建PID控制器如下：typedef struct { /* Cont.
复制链接

扫一扫