基于Simulink的Chaos混沌电路设计与仿真

最新推荐文章于 2023-09-12 20:17:32 发布

简简单单做算法

最新推荐文章于 2023-09-12 20:17:32 发布

阅读量677

点赞数 1

分类专栏： MATLAB算法开发 # 通信信号文章标签： Simulink Chaos混沌电路

本文链接：https://blog.csdn.net/aycd1234/article/details/132374538

版权

MATLAB算法开发同时被 2 个专栏收录

317 篇文章

订阅专栏

通信信号

66 篇文章

订阅专栏

本文介绍了Chua电路的理论概述，包括其作为混沌电路的特性，以及Lorenz关于混沌的定义。还提到了算法在Matlab2022a中的运行情况，并展示了部分核心程序和完整的工程实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

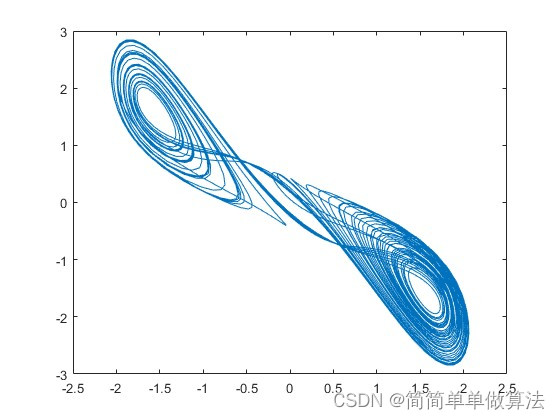
1.算法运行效果图预览

2.算法运行软件版本

matlab2022a

3.部分核心程序

07_001m

4.算法理论概述

混沌电路是一类特殊的非线性电路，其输出信号表现出无规律、非周期性、高度敏感的动态行为，这种行为通常称为混沌。混沌电路的研究始于20世纪60年代，混沌现象在数学、物理、工程等领域产生了广泛的影响。下面将详细介绍一种经典的混沌电路，即“Chua's Circuit”（Chua电路）。

混沌是非线性确定系统中由于内察随机性而产生的外在复杂表现，是一种貌似随机的伪随机运动。它的基本特征之一是系统对初始条件的极端敏感性，即初始条件的微小差异会随时间的演化呈指数增长，最终不可接受。其长期行为表现出明显的随机，不可控制和不可预测。人们对混沌现象的研究起始于70年代。被誉为“混沌之父”的美国科学家Lorenz曾经给出过一个通俗的定义:一个真实的物理系统，在排除了所有的随机性影响以后，仍有貌似随机的表现，那么这个系统就是混沌的。Lorenz这个定义说出了混沌的如下基本特征:(l)混沌是系统固有的特性。系统所表现出来的复杂性是系统自身的，内在的因素造成的，并不是在外界的干扰下所产生的，是系统内在随机性的表现。(2)混沌是具有确定性的。混沌的确定性分为两个方面:首先，混沌系统是确定的系统，是一个真实的物理系统;其次，混沌的表现是貌似随机，而并不是真正的随机，系统的每一时刻状态都受到前一状态的影响，是确定出现的，而不是像随机系统那样随意出现，混沌系统的状态是可以完全重现的，这和随机系统不同。(3)混沌系统的表现具有复杂性。混沌系统的表现是貌似随机的，它不是周期运动，也不是准周期运动，具有良好的自相关性和低频宽带的特点。

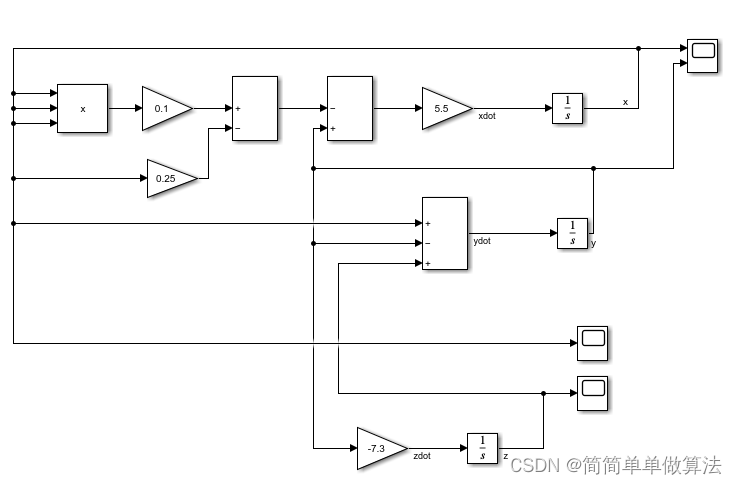
电路的状态变量由 xx, yy, zz 表示，其非线性微分方程可以写为：