LOAM系列之点云预处理理解

最新推荐文章于 2025-03-28 10:50:53 发布

北方南方2020

最新推荐文章于 2025-03-28 10:50:53 发布

阅读量1.8k

点赞数 10

分类专栏： SLAM/VIO/定位

本文链接：https://blog.csdn.net/baidu_34319491/article/details/117396349

版权

SLAM/VIO/定位专栏收录该内容

6 篇文章

订阅专栏

本文详细解读经典3D激光SLAM算法LOAM中的点云预处理步骤，包括计算点所在线束及角度、处理角度范围、判断是否过半等关键点，帮助读者理解代码逻辑。适用于velodyne16线激光雷达，通过预处理确保点云按角度排序，为后续运动补偿和匹配做准备。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

LOAM系列之点云预处理理解

文章目录

LOAM系列之点云预处理理解

LOAM作为一个非常经典的3D激光SLAM算法，一直被各种模仿和升级(

L e g o - L O A M, a - l o a m, f l o a m, l i v o x - l o a m, L i o - m a p p i n g, l i o - S A M

)等等等等，虽然升级的版本很多，但是在点云处理阶段基本都大同小异，都需要获取点云中每个点的线序以及在这一帧点云的角度，进而算出一个scale，用于后面的运动补偿和匹配上。
相信大家看代码一定会看到计算点所在的线束以及角度的这个函数，这里面有好多角度，

startOri, endOri,halfPassed,+= 2 * M_PI,-=2 * M_PI,M_PI * 3 / 2

啥啥啥的，我滴天，这些都是啥玩意儿，看网上也很少有比较详细的解读(也可能是我太菜了，之前看了半天愣是没看懂)，所以，我就抛砖引玉，做个自己的理解的分享，希望对大家有所帮助，更新不易，如有转载或其它用途，请与我联系，注明出处！如有忘了引用的参考，也请与我联系，我改正添加！

1 上代码

废话不多说，从代码开始，这里就以最经典的Loam代码来做分析，其它的应该差不太多。

void MultiScanRegistration::process(const pcl::PointCloud<pcl::PointXYZ>& laserCloudIn, const Time& scanTime)
{
  size_t cloudSize = laserCloudIn.size();

  // determine scan start and end orientations
  float startOri = -std::atan2(laserCloudIn[0].y, laserCloudIn[0].x);
  float endOri = -std::atan2(laserCloudIn[cloudSize - 1].y,
                             laserCloudIn[cloudSize - 1].x) + 2 * float(M_PI);
  if (endOri - startOri > 3 * M_PI) {
    endOri -= 2 * M_PI;
  } else if (endOri - startOri < M_PI) {
    endOri += 2 * M_PI;
  }

  bool halfPassed = false;
  pcl::PointXYZI point;
  _laserCloudScans.resize(_scanMapper.getNumberOfScanRings());
  // clear all scanline points
  std::for_each(_laserCloudScans.begin(), _laserCloudScans.end(), [](auto&&v) {v.clear(); }); 

  // extract valid points from input cloud
  for (int i = 0; i < cloudSize; i++) {
    point.x = laserCloudIn[i].y;
    point.y = laserCloudIn[i].z;
    point.z = laserCloudIn[i].x;

    // skip NaN and INF valued points
    if (!pcl_isfinite(point.x) ||
        !pcl_isfinite(point.y) ||
        !pcl_isfinite(point.z)) {
      continue;
    }

    // skip zero valued points
    if (point.x * point.x + point.y * point.y + point.z * point.z < 0.0001) {
      continue;
    }

    // calculate vertical point angle and scan ID
    float angle = std::atan(point.y / std::sqrt(point.x * point.x + point.z * point.z));
    int scanID = _scanMapper.getRingForAngle(angle);
    if (scanID >= _scanMapper.getNumberOfScanRings() || scanID < 0 ){
      continue;
    }

    // calculate horizontal point angle
    float ori = -std::atan2(point.x, point.z);
    if (!halfPassed) {
      if (ori < startOri - M_PI / 2) {
        ori += 2 * M_PI;
      } else if (ori > startOri + M_PI * 3 / 2) {
        ori -= 2 * M_PI;
      }

      if (ori - startOri > M_PI) {
        halfPassed = true;
      }
    } else {
      ori += 2 * M_PI;

      if (ori < endOri - M_PI * 3 / 2) {
        ori += 2 * M_PI;
      } else if (ori > endOri + M_PI / 2) {
        ori -= 2 * M_PI;
      }
    }

    // calculate relative scan time based on point orientation
    float relTime = config().scanPeriod * (ori - startOri) / (endOri - startOri);
    point.intensity = scanID + relTime;

    projectPointToStartOfSweep(point, relTime);

    _laserCloudScans[scanID].push_back(point);
  }

  processScanlines(scanTime, _laserCloudScans);
  publishResult();
}

2 多线激光雷达简简单单介绍

预处理的代码核心就在这个函数里面，在讲解代码之前，做个关于多线激光雷达的说明，因为代码中用的是velodyne16线的激光雷达，拥有16个激光发射器，对于机械式雷达来说，这16个发射器会同时保持固定的相对位置一起绕着雷达中心轴旋转。
在这里插入图片描述
主视图和俯视图如上面所示，左边是简化的结构，注意，实际上，激光发射器，不是从原点发射出去的，这里只是为了简化说明，实际的雷达激光发射器会在中轴线附近按照一定的俯仰角度排布，只不过根据激光接收的数据反解算到了雷达中心坐标系下；图中雷达是顺时针旋转，需要注意的是，有可能也可以是逆时针旋转的，这个每个型号可能不一样，但是只要开机了就会一直朝着一个方向转。
俯视图里，首先，图里面的scan1,scan2,scan3表示不同的激光发射器打在地面上形成的圆环，如果不是地面上，那就不是同心圆了，其中，红色的点表示这一根线的开始点，绿色表示这一根线的终点，这里再补充说明一下，就是对于不同线束的多线激光雷达，内部的激光发射器排布方式不统一，如，16线有可能是所有激光发射器在统一纵向平面，且水平朝向一致，32线就有可能出现激光发射器不在同一平面的情况，也就是右图中会出现scan2和scan1的起点相对于雷达xy坐标水平角度不一致的情况；再有，雷达根据分帧方式的不同，可能会出现一帧的点云里覆盖的角度不止360°的情况，就会出现终点在起点前面的情况，也就是图中的scan3，当然，对于同一颗雷达，scan1和scan2可能同时发生，scan3和scan1是不能同时发生的，否则雷达就有问题了，因为大家如果用sensor_msgs::PointCloud2消息，或者pcl::PointCloud<T>的时候，都会发现数据里有个width和height，这个height就是线束，而这个width 就是每根线一圈的采样点，不管怎么排布激光头，它们转动的角度都是一样的，所以采样点也得一样。总之，不管怎么样的方式，Loam里的处理都能很好地解决。

3 代码解读

3.1 起始结束点

这里基于顺时针的旋转方向来讨论。

float startOri = -std::atan2(laserCloudIn[0].y, laserCloudIn[0].x);
float endOri = -std::atan2(laserCloudIn[cloudSize - 1].y,
                             laserCloudIn[cloudSize - 1].x) + 2 * float(M_PI);
if (endOri - startOri > 3 * M_PI) {
    endOri -= 2 * M_PI;
   } else if (endOri - startOri < M_PI) {
    endOri += 2 * M_PI;
}
bool halfPassed = false;

首先看代码里面的这一段，判断起始点的角度，很好奇的是为什么要再atan2函数前面乘一个负号，实际上，根据代码，画出来就可以明白了，首先，我们知道，atan2的取值范围是(-pi,pi)，那么-atan2的取值范围也是(-pi,pi)，看起来好像没有什么区别，实际上对应到点云去看，就会发现端倪。这里拿scan1来进行说明，红色是起点，按照atan2算出来，应该是一个接近pi的数值，绿色是终点，按照atan2算出来，应该是一个接近-pi的数值，都乘了负号，那么结果就反过来了，也就是说，在雷达的左半边，角度是(-pi,0)，右半边是(0,pi)，为了方便，下图画出了一维坐标轴，其中，红色的线段部分表示雷达左边那边，绿色的线段部分表示雷达的右半边。整个坐标轴的范围是(-pi,3pi)，halfPassed仅仅表示是否转过了一半了。红色正方形表示起点，绿色正方形表示计算的终点，绿色心形表示最终计算的终点。
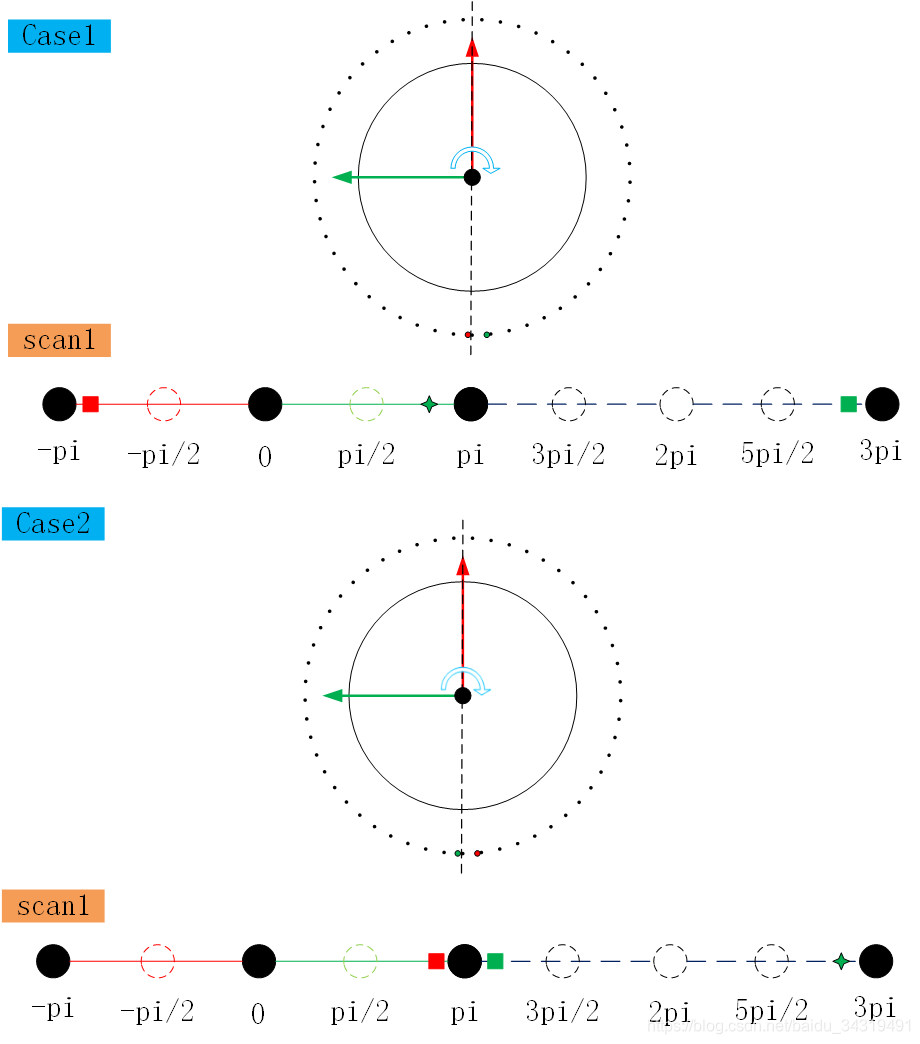
在这里插入图片描述
如图上两种情况，首先，对于case1，红色的正方形表示计算出的startOri位置，绿色的表示计算出的endOri，此时，endOri - startOri>3pi，所以，实际的终点应该-2pi，在绿色心形的位置，然后对于case2，同样的道理，只不过此时endOri - startOri<pi，所以，实际的终点应该+2pi，在绿色心形的位置，当然，大家可以考虑scan3的道理，去绘制相应的结果。所以从这里就可以看出，作者是希望能将一帧中每一根光束内的所有的点云，按照角度从小到大的排序，这样很方便后面判断是不是过半了，不得不说这种方法很巧妙。

// calculate horizontal point angle
    float ori = -std::atan2(point.x, point.z);
    if (!halfPassed) {
      if (ori < startOri - M_PI / 2) {
        ori += 2 * M_PI;
      } else if (ori > startOri + M_PI * 3 / 2) {
        ori -= 2 * M_PI;
      }

      if (ori - startOri > M_PI) {
        halfPassed = true;
      }
    } else {
      ori += 2 * M_PI;

      if (ori < endOri - M_PI * 3 / 2) {
        ori += 2 * M_PI;
      } else if (ori > endOri + M_PI / 2) {
        ori -= 2 * M_PI;
      }
    }

接下来就是对每个点进行计算了，其实弄懂了上面的东西，下面这些内容就很容易看明白了，首先，对于没有过半的情况，如果某个点的角度ori < startOri - M_PI / 2，那么这个实际上对应的就是上面图中的case2的情况，即出现了跨区间，那么此时，就要将角度加上一个周期，这样才能保证点云的连续性，反之，如果是ori > startOri + M_PI * 3 / 2，那么实际上就是对应着case1中的情况，一直到要过半了的情况。

3.1 中间点-未过半

if (!halfPassed) {
      if (ori < startOri - M_PI / 2) {
        ori += 2 * M_PI;
      } else if (ori > startOri + M_PI * 3 / 2) {
        ori -= 2 * M_PI;
      }

      if (ori - startOri > M_PI) {
        halfPassed = true;
      }
    }

3.2 中间点-过半

else {
      ori += 2 * M_PI;

      if (ori < endOri - M_PI * 3 / 2) {
        ori += 2 * M_PI;
      } else if (ori > endOri + M_PI / 2) {
        ori -= 2 * M_PI;
      }
    }

对于过半了的情况，首先要做的就是要先加上一个2pi，让点云的角度落在比起始角度大的区间内，如果说ori < endOri - M_PI * 3 / 2，这时对应的是case2的情况，而且这个点是转过一圈后落在雷达的左半边的，因为只有这样， $\in (pi,3pi/2)$ ，但是实际上是已经很靠近终点的了，所以要加上2pi才能得到正确的比例。相反，如果ori > endOri + M_PI / 2，这时对应的是case1的情况，此时雷达就转过了半圈，点落在雷达的右半边， $\in (2pi+dx,3pi)$ ，其中dx是起点相对于-pi的绝对角度差，此时都比endOri + M_PI / 2要大，所以要减去2pi。
个人认为，其实这里做了个限定，就是认为一帧雷达最多转过的角度为360+90=450°，所以才会有pi/2,3pi/2这些角度。