梯度下降：从牛顿法到LM法

首先，本文大部分思路取自b站视频：三维重建第九课：LM（二）优化方法演进。

在介绍牛顿法之前，笔者要先聊一下最经典的梯度下降法。

对目标函数的目标点处进行求导，所得的方向就是梯度下降的方向。

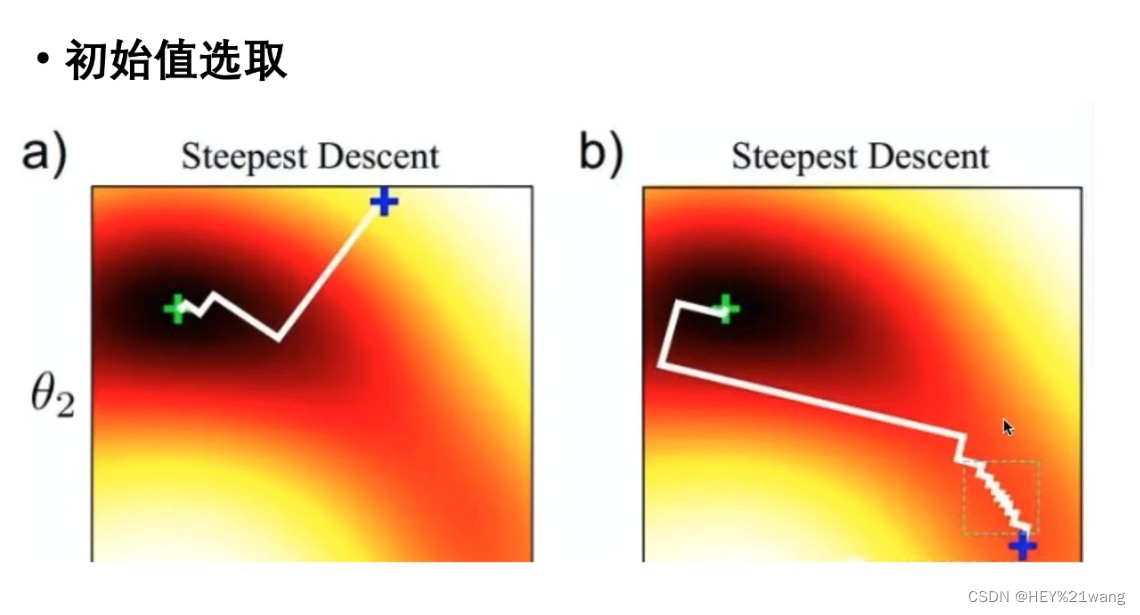 但是梯度下降方法的缺点也十分明显，如果初始值选取的位置不理想就可能使迭代次数大幅增加，影响效率。 

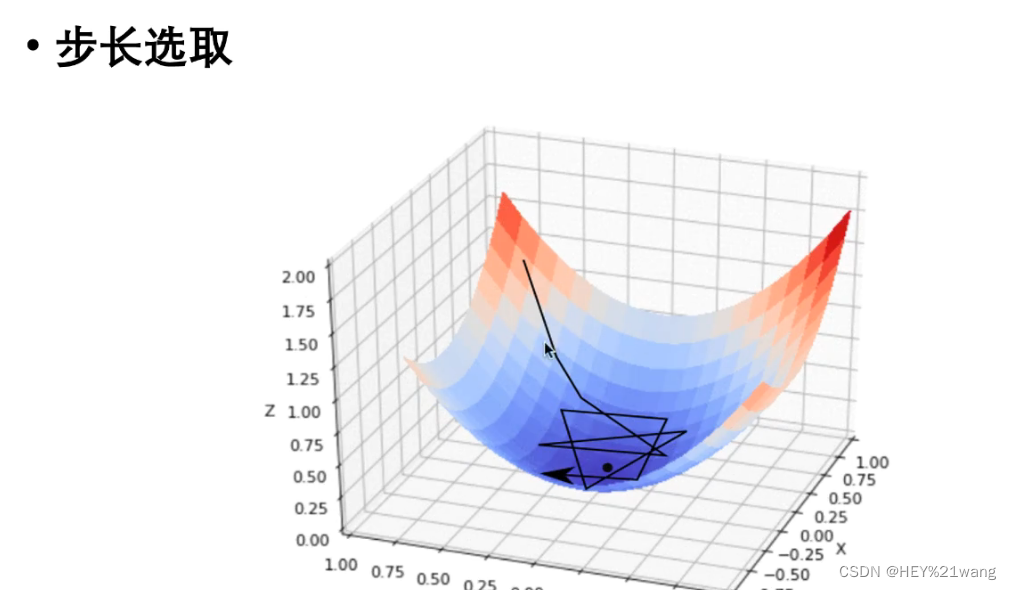同时，梯度下降的步长选取也是一个问题，如果步长选取过小会导致迭代次数增加，步长选取过长就会导致上图的情况，无法获得最优解。 

牛顿法：

J(x)为雅克比矩阵，H(x)为海森矩阵

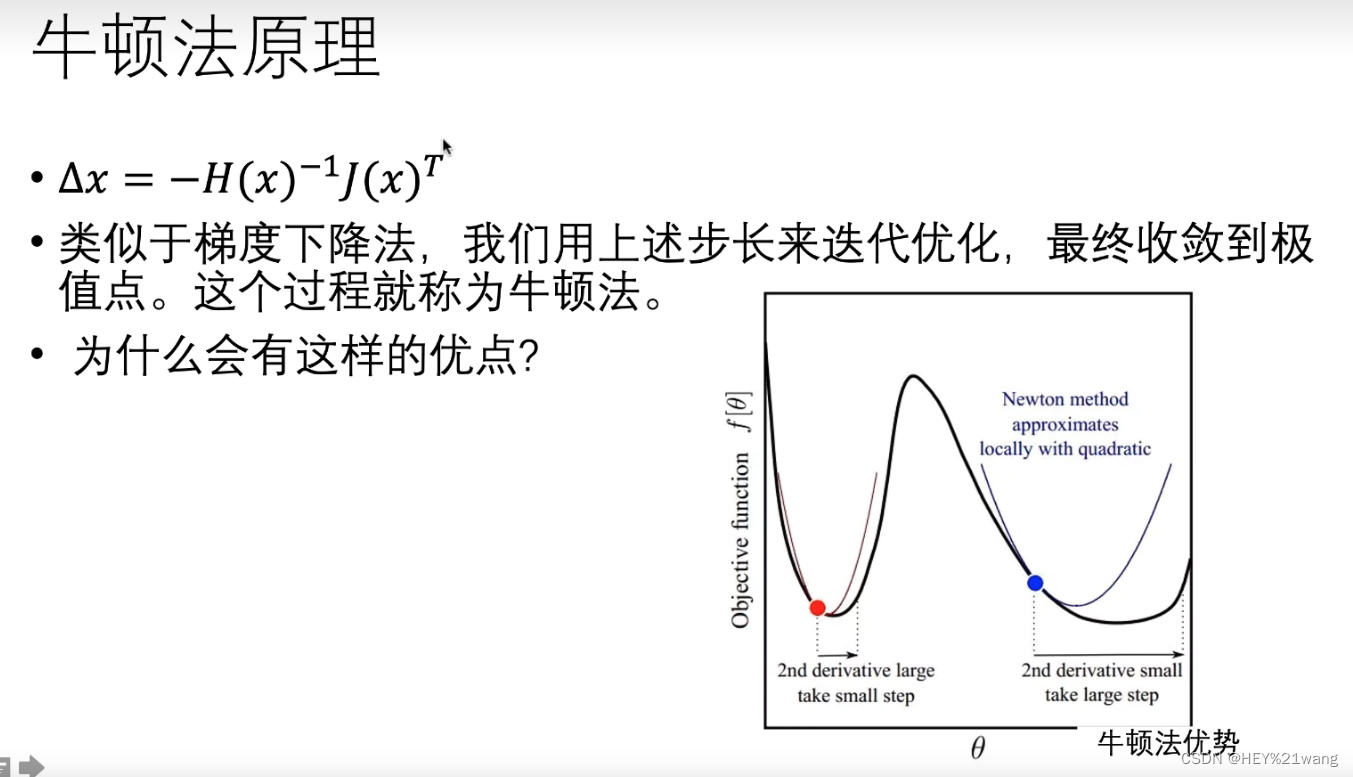
 牛顿法的优势是：在曲率变化大时（红点处），H(x)变大，这样步幅△x变小，在曲率变化小时（蓝点处）△x变大，这样就可以保证在保证了效率的同时具有良好的鲁棒性。

缺点就是求海森矩阵的计算量太大了。

 高斯牛顿法将J(x)TJ(x)近似等于H(x)

LM算法：

 u取值较大时，我们可以将LM算法看做是一阶的梯度下降方法。当u取值较小时，我们可以将LM算法看成高斯牛顿法。这种方法牺牲了效率但是更加的鲁棒。

LM算法的核心思想是在每次迭代中，用一个二次函数来近似目标函数，并在该二次函数上求解最优步长。

LM算法的迭代公式为：

xk+1​=xk​−(Jk⊤​Jk​+μI)−1gk​

其中，xk​是第k次迭代的参数向量，Jk​是目标函数关于参数的雅可比矩阵，gk​是目标函数关于参数的梯度向量，μ是一个正则化因子，I是单位矩阵。

如果步长Δx过大，会导致目标函数的值增大，而不是减小。这时候，我们需要调整μ的值，使得步长变小，从而保证目标函数的下降。

根据LM算法的迭代公式，我们可以看到，当μ很大时，(Jk⊤​Jk​+μI)−1接近于I/μ，那么步长就变成了

Δx≈−1/μ​*gk​

这相当于最速下降法的步长，而最速下降法的步长随着μ的增大而减小。

因此，如果步长过大导致判断值p远远小于1，那么此时应当将置信区间减少，也就是将μ增大，从而缩小步长，使得目标函数能够有效地下降。