CS231n 卷积神经网络与计算机视觉 9 卷积神经网络结构分析

终于进入我们的主题了ConvNets或者CNNs，它的结构和普通神经网络都一样，之前我们学习的各种技巧方法都适用，其主要不同之处在于：
ConvNet假定输入的是图片，我们根据图片的特性对网络进行设定以达到提高效率，减少计算参数量的目的。

1. 结构总览

首先我们分析下传统神经网络对于图片的处理，如果还是用CIFAR-10上的图片，共3072个特征，如果普通网络结构输入那么第一层的每一个神经单元都会有3072个权重，如果更大的像素的图片进入后参数更多，而且用于图片处理的网络一般深度达10层之上，加在一起参数的量实在太大，参数过多也会造成过拟合，而且图片也有自身的特点，我们需要利用这些特点，将传统网络改革，加快处理速度和精确度。
我们注意到图片的像素是由3个通道构成的，我们就利用了这个特点将其神经元安置到了三维空间（width, height, depth），分别对应着图片的32x32x3（以CIFAR为例）如下图：

红色是输入层这里的深度是3，输出层是1x1x10的结构。其他几层的含义后面会介绍，现在先知道每层都是height × width × depth结构。

2. 卷积神经网络的层

卷积神经网络有三种层：卷积层、池化层和全连接层（Convolutional Layer, Pooling Layer, 及 Fully-Connected Layer）。
以处理CIFAR-10的卷积神经网络为例，简单的网络应包含这几层：
[INPUT - CONV - RELU - POOL - FC]也就是[输入-卷积-激活-池化-分类得分]，各层分述如下：

• INPUT [32x32x3] 输入长32宽32带有三个通道的图片
• CONV ：计算图片的局部区域，如果我们想要使用12个过滤器fliters，他的体积将是 [32x32x12].
• RELU ：还是一个激励层max(0,x) ，尺寸还是 ([32x32x12]).
• POOL： 沿着图片的(width, height)采样, 减小长宽的维度，例如得到的结果是 [16x16x12].
• FC (i.e. fully-connected) 计算分类得分最终尺寸是 [1x1x10], 这层是全连接的，每一个单元都与前一层的各个单元连接。

注意：
1. 卷及神经网络包含不同的层 (e.g. CONV/FC/RELU/POOL 也是最受欢迎的)
2. 每一层都输入输出3d结构的数据，除了最后一层
3. 有些层可能没有参数，有些层可能有参数 (e.g. CONV/FC do, RELU/POOL don’t)
4. 有些层可能有超参数有些层也可能没有超参数(e.g. CONV/FC/POOL do, RELU doesn’t)
下图是一个例子，没法用三维表示只能展成一列的形式了。

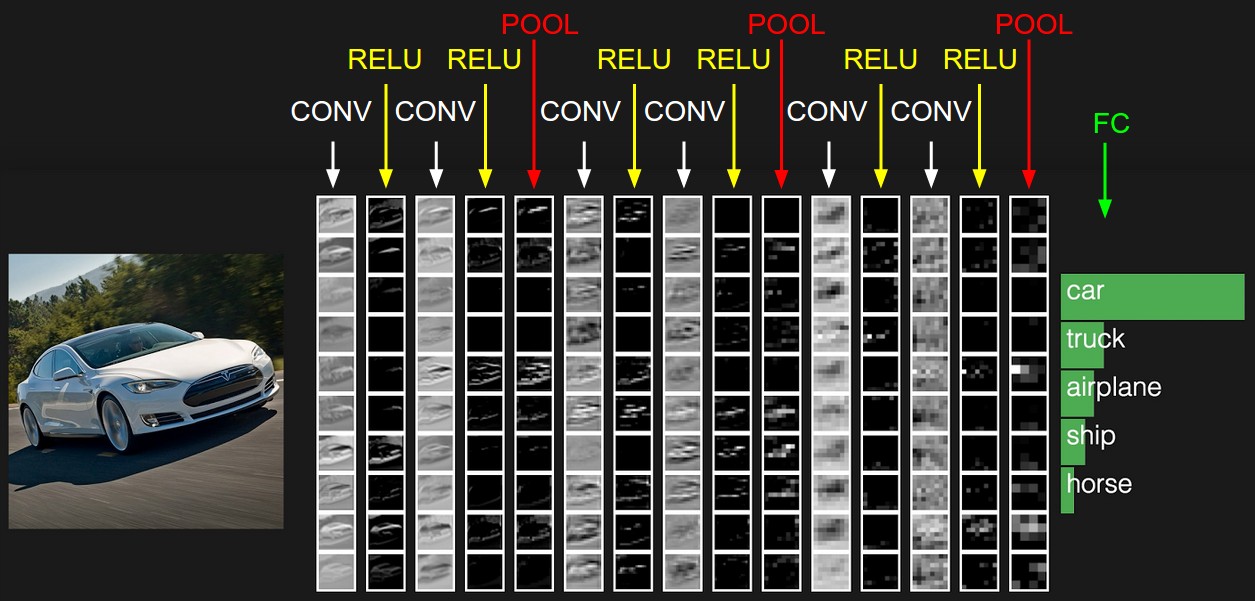
下面展开讨论各层具体细节：

2.1 卷积层

卷积层是卷积神经网络的核心层，大大提高了计算效率。
卷积层由很多过滤器组成，每个过滤器都只有一小部分，每次只与原图像上的一小部分连接，UFLDL上的图：

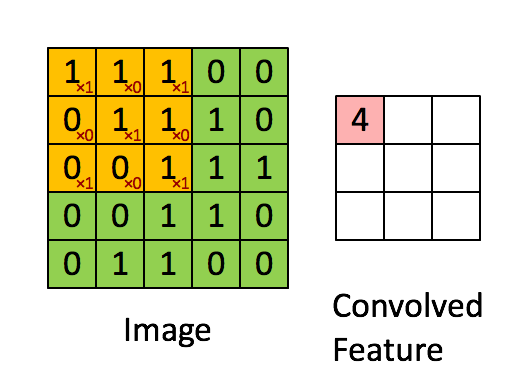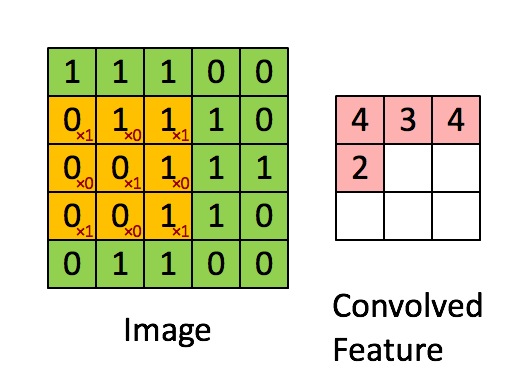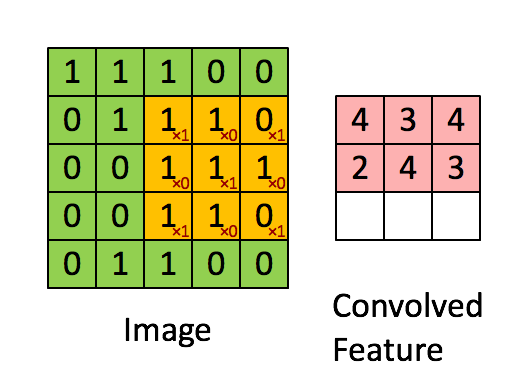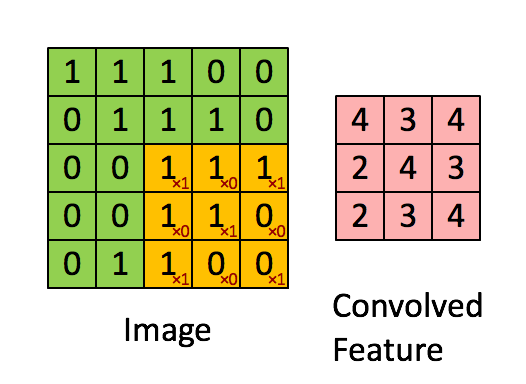
这是一个过滤器不停滑动的结果，
我们这里要更深入些，我们输入的图像是一个三维的，那么每个过滤器也是有三个维度，假设我们的过滤器是5x5x3的那么我们也会得到一个类似于上图的激活值的映射也就是convolved feature 下图中叫作 activion map,其计算方法是$w^T\times x+b$其中w是5x5x3=75个数据，也就是权重，他是可以调节的。
我们可以有多个过滤器：

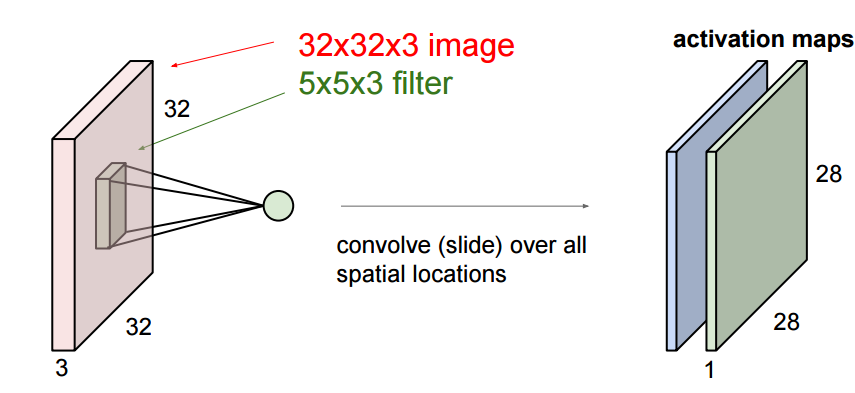
更深入一些，当我们滑动的时候有三个超参数：
1. 深度，depth，这是过滤器的数量决定的。
2. 步长，stride，每次滑动的间隔，上面的动画每次只滑动1个数，也就是步长为1.
3. 补零数， zero-padding，有时候根据需要，会用零来拓展图像的面积，如果补零数为1，变长就＋2，如下图中灰色的部分就是补的0

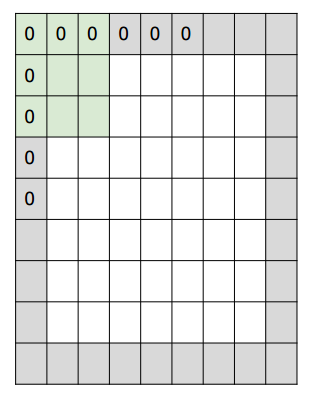
下面是一个一维的例子：

其输出的空间维度计算公式是

$$(W - F + 2P)/S + 1$$
其中w是输入的尺寸，f是过滤器的尺寸，p是补零的尺寸，s是步长，图中如果补零为1那么输出为5个数，步长为2输出为3个数。
到现在为止我们好像都没有涉及到 神经这个概念哇，现在我们就从神经角度来理解：
上面提到每一个激活值都是： $w^T\times x+b$，这个公式我们熟悉哇，这就是神经元的得分公式呀，所以我们可以将每一个 activation map 其看做是一个filter的杰作，如果有5个过滤器，就会有5个不同的filter同时连接一个部分。
卷积神经网络还有一个重要的特征： 权重共享：在同一个filter上的不同的神经单元（滑动窗口）的权重是相同的。这样以来大大减少了权重的数量。
这样每一层权重相同，每一个过滤器计算的结果都是一个卷积（后来还会加一个偏差b）:

这也是卷积神经网络的名字的来源。
下面这张图是错误的，请看官网 http://cs231n.github.io/convolutional-networks/#conv，找出其中的错误就明白卷积的工作原理了。

（gif来自寒小阳的 博客）
虽然这里吧每一个filter的权重w变为而来三部分，但是在神经元里还是用了wx+b的形式。
- 反向传播：这种卷积的反向传播还是卷积，计算过程也比较简便
- 1x1 convolution：一些文章用了1*1的卷积, 比如最开始的 Network in Network. 这样可以有效的做多个内积， 输入有三层，那么每层至少要有三个w，也就是把上面的动态图的filter变为1x1x3.
-Dilated convolutions.最近又有研究( e.g. see paper by Fisher Yu and Vladlen Koltun) 对卷积层添加了一个超参数：dilation。这是对filter的进一步控制，我们开一下效果：dilation等于0时，这样计算卷积w[0]x[0] + w[1]x[1] + w[2]x[2]；dilation =1时变成了这样w[0]x[0] + w[1]x[2] + w[2]x[4];也就是我们要处理的图像中每个隔了个1. 这就允许了利用更少的层来融合空间信息. 例如我们用了两个 3x3 CONV layers在最顶层 ，这是第二层起到了 感受5x5 （ effective receptive field）的作用. 如果使用dilated convolutions 那么这个effective receptive field会以指数形式增长.

2.2 池化层

上面可以知道在卷积层之后得到的结果还是挺多，而且由于滑动窗口的存在，很多信息也有重合，于是有了池化pooling 层，他是将卷积层得到的结果无重合的分来几部分，然后选择每一部分的最大值，或者平均值，或者2范数，或者其他你喜欢的值，我们以取最大值的max pool为例：

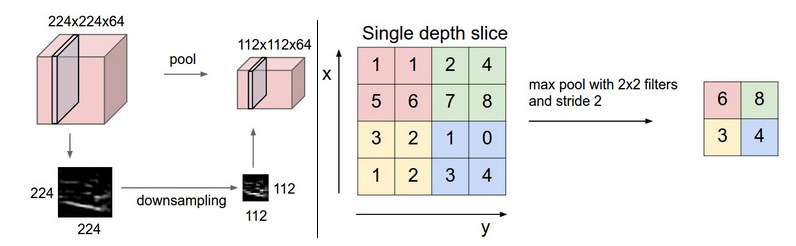
- 反向传播：最大值的梯度我们之前在反向传播的时候就已经学习过了，这里一般都跟踪最大的激活值，这样在反向传播的时候会提高效率.
- Getting rid of pooling. 一些人认为pooling是没有必要的，如The All Convolutional Net ，很多人认为没有池层对于生成式模型（generative models）很重要，似乎以后的发展中，池层可能会逐渐减少或者消失。

2.3 其他层

1. Normalization Layer，以前的时候用normalization 层的模拟人脑的抑制作用，但是逐渐认为没有多大的帮助，于是用的少了，这篇论文里有介绍其作用 Alex Krizhevsky’s cuda-convnet library API.
2. Fully-connected layer，这个全连接层和以前学过的一样，前面提到过最后的分类层是全连接层。

2.4 Converting FC layers to CONV layers

全连接层和卷积层除了连接方式不一样，其计算方式都是内积，可以相互转换：
1. FC如果做CONV layer 的工作就相当于其矩阵的多数位置都是0（稀疏矩阵）。
2. FC layer 如果被转变为 CONV layer. 相当于每一层的局部连接变为了全部链接如FC layer with K=4096的输入是7×7×512那么对应的卷积层为 F=7,P=0,S=1,K=4096输出为1×1×4096。
例子：
假设一个cnn输入 224x224x3图像,经过若干变化之后某一层输出 7x7x512 到这里之后使用两4096的FC layer及最后一个1000的FC计算分类得分下面是把这三层fc转化为Conv 的过程:
1. 使用 F=7的conv layer 输出为 [1x1x4096]；
2. 使用F=1的过滤器，输出为 [1x1x4096]；
3. 使用F=1的卷积层，输出为 [1x1x1000]。

每次转化都会将FC的参数转变为conv的参数形式. 如果在转变后的系统中传入更大的图片，也会非常快速的向前运算。例如将384x384的图像输入上面的系统，会在最后三层之前得到[12x12x512]的输出, 经过上面转化的conv 层会得到 [6x6x1000], （(12 - 7)/1 + 1 = 6）. 我们一下就得出了6x6的分类结果。
这样一次得到的比原来使用迭代36次得到的要快。这是实际应用中的技巧。
另外我们可以用两次步长16的卷积层代替一次步长为32的卷积层来输入上面的图片，提高效率。

3 搭建卷积神经网络

下面我们就用CONV, POOL，FC ，RELU 搭建一个卷积神经网络：

3.1 层次结构

我们按照以下结构搭建

INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC

其中N >= 0 (一般N <= 3), M >= 0, K >= 0 (一般K < 3).
这里要注意：我们更倾向于使用多层小size的CONV。
为什么呢？
比如3个3x3的和一个7x7的conv层，他们都可以 得到7x7的receptive fields.但是3x3的有以下优点：
1. 3层的非线性组合要比一层线性组合表达能力强；
2. 3层小尺寸的卷积层的参数数量要少，3x3x3<7x7；
3. 反向传播中我们需要使用更多的内存来储存中间层结果。

值得注意的是Google’s Inception architectures 及Residual Networks from Microsoft Research Asia. Both 等创造了相比以上结构更加复杂的连接结构。

3.2 层的大小

1. 输入层：输入层一般是2的指数形式比如 32 (e.g. CIFAR-10), 64, 96 (e.g. STL-10), or 224 (e.g. common ImageNet ConvNets), 384, 512等.
2. 卷积层：一般是小的过滤器比如3x3或者最大 5x5，步长设为1，当加入补零时卷积层可能不会改变输入的尺寸，如果必须使用大的过滤器，那么经常在第一层使用补零的方法P=(F−1)/2。
3. 池化层：常见的设置是使用2x2的最大池化层，很少有超过3x3的最大池化层。
4. 如果我们的步长大于1或者没有补零，我们需要非常注意看是否我们的步长和顾虑器是否足够健壮，我们的网络是否均匀对称连接。
5. 步长为1表现更好，对池化也更有兼容新.
6. 补零的好处：如果不补零那么边缘的信息会很快被抛弃
7. 要考虑到电脑的内存限制。例如输入 224x224x3 图片，过滤器为 3x3 共64 filters，padding 为1 这样每张图片需要72MB 内存 ，但是GPU上运行的话，内存可能不够所以可能会调整下参数比如 filter为 7x7，stride 为 2 (ZF net). 或者filer11x11 ， stride of 4.（AlexNet）

3.3 案例

1. LeNet. 第一个成功应用的cnn（ Yann LeCun in 1990’s）. 他的强项是杜zip codes, digits, etc.
2. AlexNet. 第一个广泛的应用于计算机视觉, （by Alex Krizhevsky, Ilya Sutskever and Geoff Hinton）. ImageNet ILSVRC challenge in 2012 大放异彩，与LeNet结构类似不过更深更大，多层卷积层叠加。
3. ZF Net. The ILSVRC 2013 winner （ Matthew Zeiler and Rob Fergus）. It became known as the ZFNet (short for Zeiler & Fergus Net).调整了Alexnet的结构参数, 扩大了中间卷积层 使第一层的过滤器和步长都减小了.
4. GoogLeNet. The ILSVRC 2014 winner（Szegedy et al. from Google.） 极大的减少了参数数量 (由 60M到4M). 使用Average Pooling代替了 ConvNet的第一个FC层, 消除了大量的参数，有很多的变体如：Inception-v4.
5. VGGNet. The runner-up in ILSVRC 2014 （ Karen Simonyan and Andrew Zisserman ）证明了深度的好处. 可以在Caffe上使用. 但是参数太多，(140M)，计算量大 . 不过现在已经正实有很多不需要的参数可以去除。
6. ResNet. （Kaiming He et al）.winner of ILSVRC 2015. 截止2016年5月10，这是一种最先进的模型. 现在也有了改进版 Identity Mappings in Deep Residual Networks (published March 2016).
   其中VGG的计算花费为：

INPUT: [224x224x3]        memory:  224*224*3=150K   weights: 0
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*3)*64 = 1,728
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*64)*64 = 36,864
POOL2: [112x112x64]  memory:  112*112*64=800K   weights: 0
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128]  memory:  56*56*128=400K   weights: 0
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256]  memory:  28*28*256=200K   weights: 0
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512]  memory:  14*14*512=100K   weights: 0
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512]  memory:  7*7*512=25K  weights: 0
FC: [1x1x4096]  memory:  4096  weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096]  memory:  4096  weights: 4096*4096 = 16,777,216
FC: [1x1x1000]  memory:  1000 weights: 4096*1000 = 4,096,000



TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parameters

注意到内存使用最多的时候在开始几个CONV layers, 参数基本都在最后几个FC层第一个FC有100M个！

3.4 内存使用

内存主要在以下几个方面消耗较多
1. 大量的激活值和梯度值。测试时可以只储存当前的激活值丢弃之前的在下方几层激活值会大大减少激活值的储存量。
2. 参数的储存，在反向传播时的梯度及使用 momentum, Adagrad, or RMSProp时的缓存都会占用储存，所以估计参数使用的内存时一般至少要乘以3倍
3. 每次网络运行都要记住各种信息比如图形数据的批量等
如果估计网络需要的内存太大，可以适当减小图片的batch，毕竟激活值占用了大量的内存空间。

其他资料

1. Soumith benchmarks for CONV performance
2. ConvNetJS CIFAR-10 demo 浏览器的ConvNets实时演示.
3. Caffe,流行的ConvNets工具
4. State of the art ResNets in Torch7

总结