生成扩散模型漫谈：DDPM = 贝叶斯 + 去噪

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

到目前为止，笔者给出了生成扩散模型 DDPM 的两种推导，分别是《生成扩散模型漫谈：DDPM = 拆楼 + 建楼》中的通俗类比方案和《生成扩散模型漫谈：DDPM = 自回归式 VAE》中的变分自编码器方案。两种方案可谓各有特点，前者更为直白易懂，但无法做更多的理论延伸和定量理解，后者理论分析上更加完备一些，但稍显形式化，启发性不足。

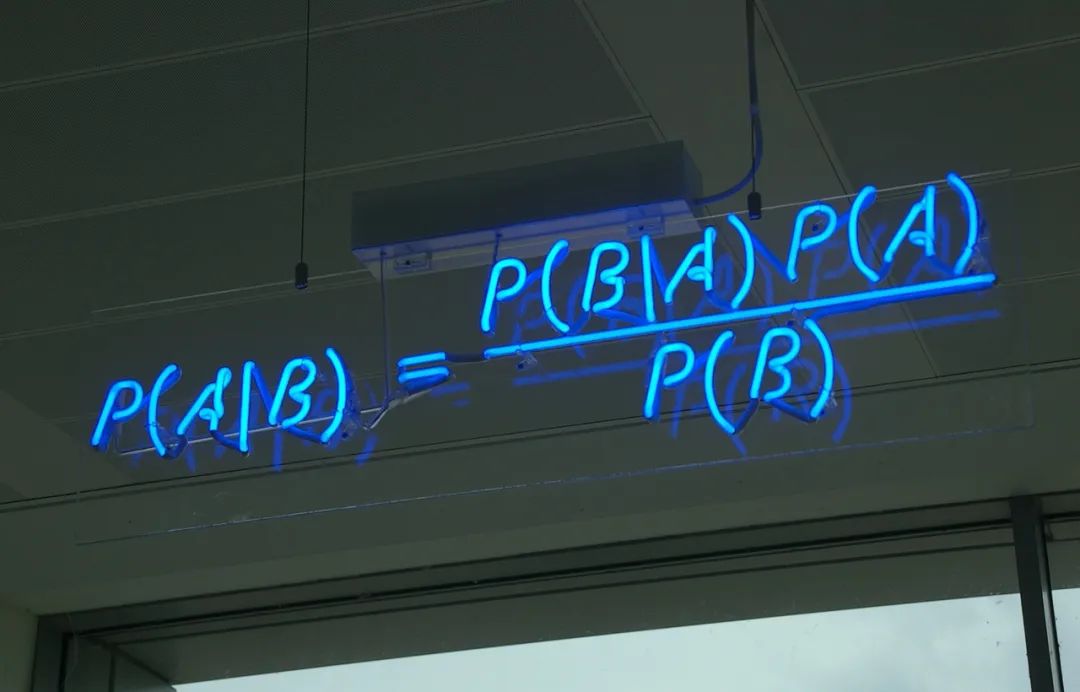
▲ 贝叶斯定理（来自维基百科）

在这篇文章中，我们再分享 DDPM 的一种推导，它主要利用到了贝叶斯定理来简化计算，整个过程的“推敲”味道颇浓，很有启发性。不仅如此，它还跟我们后面将要介绍的 DDIM 模型 [1] 有着紧密的联系。

模型绘景

再次回顾，DDPM 建模的是如下变换流程：

其中，正向就是将样本数据 逐渐变为随机噪声 的过程，反向就是将随机噪声 逐渐变为样本数据 的过程，反向过程就是我们希望得到的“生成模型”。

正向过程很简单，每一步是

或者写成

402 Payment Required

。在约束 之下，我们有

从而可以求出

402 Payment Required

，其中 ，而 。

DDPM 要做的事情，就是从上述信息中求出反向过程所需要的 ，这样我们就能实现从任意一个 出发，逐步采样出 ，最后得到随机生成的样本数据 。