即插即用！美团提出整数量化系数方案：大模型细粒度量化的免费午餐

最新推荐文章于 2024-12-11 09:58:24 发布

PaperWeekly

最新推荐文章于 2024-12-11 09:58:24 发布

阅读量1k

点赞数 21

文章标签：人工智能机器学习深度学习算法

本文链接：https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/140257268

版权

摘要

该文提出“整型量化系数”（Integer Scale），这是一种新颖的训练后量化方案，专门针对大型语言模型，它有效地解决了当前细粒度量化方法中的推理瓶颈，并且几乎精度无损。由于它不需要额外的校准或微调，可以即插即用，适用于大多数细粒度量化方法，因此称作“免费的午餐”。它的可以最高将原始对应版本的端到端速度提升 1.85 倍，并且保持相当的精度。

此外，由于提出的整型量化系数和细粒度量化的协同作用，该文解决了 Mixtral-8x7B 和 LLaMA-3 模型的量化难题，和 FP16 精度的版本相比，端到端速度分别提高了 2.13 倍和 2.31 倍。

论文标题：

Integer Scale: A Free Lunch for Faster Fine-grained Quantization of LLMs

论文链接：

https://arxiv.org/abs/2405.14597

简介

优化大型语言模型（LLMs）的推理效率不是一项简单的任务。LLMs 通常包括一个计算密集型的预填充阶段（prefill）和一个访存密集型的自解码阶段（self-decoding）。利用整数矩阵乘法可以加速计算，但直接应用训练后量化通常会带来较大的性能下降。像 LLM-QAT [28] 这样的量化感知训练方法需要昂贵的计算资源来微调所有权重。相比之下，训练后量化成本更低，通常在实践中使用。

例如，SmoothQuant [48] 将激活量化难度迁移到权重量化，以提高量化精度。最近，细粒度的分组量化经常作为减少量化误差的手段，如 ZeroQuant [49]，GPTQ [14]，AWQ [26] 和 FPTQ [24]。

FPTQ 提出了一种细粒度的 W4A8 策略，作为 W4A16 和 W8A8 之间的折衷方案。尽管其高量化精度得益于细粒度量化，但由于细粒度所引入的内在计算复杂性，实际的推理收益也被低效的运算所吞噬，见图 1 绿色。而该文提出的整形量化系数则可以避免低效的运算，并取得实际的加速收益，见图 1 红色。该方法对 LLaMA-2 系列的 3 个模型均取得了明显的加速收益。

▲ 图1：在 LLaMA-2 模型上，W4A8（整型量化系数）与 W4A8（浮点比例因子）以及 W4A16（Marlin）的端到端延迟比较。加速比标注在条形图的顶部。

该方法有三个主要贡献点：

揭示了细粒度大型语言模型（LLM）量化方法的内在推理瓶颈，并找到了一种几乎不损失精度的解决方案，称为整数量化系数（Integer Scale）。该方法可以作为即插即用的插件，用于最先进的量化方法（例如 GPTQ [14]，AWQ [26]，Omniquant [41]，QuaRot [3] 等），并且只需做最小的修改。
细粒度量化和整数量化系数方案的结合不仅保留了现有方法的性能，还有效地解决了使用混合专家技术构建的 Mixtral [18] 和 LLaMA-3 [1] 的量化难题。
当整型量化系数应用于细粒度 W4A8 范式时，与 FP16 相比，实现了最多 1.85 倍的端到端速度提升，与 Marlin W4A16 [13] 相比提升了 1.17 倍，与浮点量化系数版本相比提升了 1.83 倍，同时在性能上是可比的，即实现了速度与精度的新帕累托前沿，证实了方法的可行性。

动机

3.1 细粒度方法能显著提升量化精度

细粒度方法 [24, 26, 52] 在许多最先进的大型语言模型（LLM）量化方法中具有显著优势。在极端情况下，即使粗粒度方法失败，它也能产生合理的结果。它可以作为插件方法应用，以提高现有方法的准确性。细粒度权重激活量化 GEMM 的输出可以写成：

其中， W 代表权重矩阵， X 代表激活矩阵，GEMM 代表矩阵乘法和累加操作。细粒度量化通常涉及将权重和激活值分别量化，这可以提高量化后的模型在保持精度方面的表现。通过这种方式，细粒度量化方法能够在量化过程中更精细地控制数值表示，从而在一定程度上减少量化误差，提高模型的整体性能。

3.2 细粒度方法存在推理瓶颈

尽管细粒度量化能够实现更高的精度，正如 [24] 中所展示的，该文发现它在推理过程中特别慢，这在双粒度量化（Dual-Granularity Quantization, DGQ）方法 [51] 中也有所记录。使用较低位宽的优势常常被它们引入的计算开销所抵消。

图 2 比较了在典型推理批量大小下的内核延迟（从 3.15 倍下降到 0.5 倍）。值得注意的是，与 FP16 相比，细粒度内核在较大的批量大小下明显更慢，这使得它在部署上不太实用。进一步分析证实，细粒度方法本质上需要大量昂贵的类型转换。如图 3（b）所示，每次整数矩阵乘法的结果都必须转换为浮点精度，以便与相应的浮点量化系数相乘。

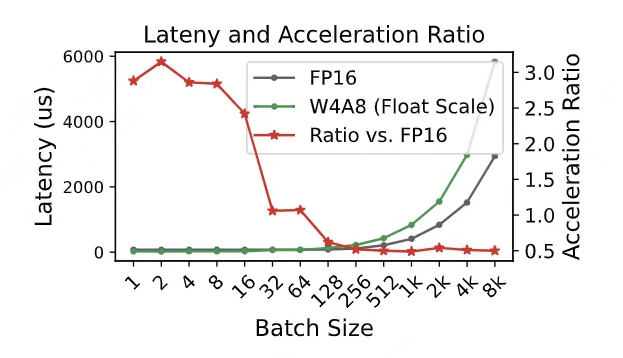
▲ 图2：W4A8 带浮点缩放与 FP16 的内核延迟比较。红线表示其相对于 FP16 的加速比率。

这种转换过程不仅增加了计算负担，特别是在处理大型批量数据时，还可能成为推理速度的瓶颈。因此，虽然细粒度量化在理论上可以提供更高的精度，但在实际应用中，它需要与推理效率之间进行权衡。解决这一问题的方法可能包括优化量化算法以减少类型转换的需求，或者开发新的量化策略，这些策略需要在不牺牲推理速度的情况下提供可接受的精度水平。

方法

▲ 图3：（a）细粒度量化将大小为 M×K 的激活 X 和大小为 K×N 的权重划分为组，以进行独立的量化。（b）以前的浮点比例因子方案需要大量的昂贵类型转换（I32toF32），这些转换来自分组矩阵乘法的结果，这阻碍了整体性能。该文提出的方案（c）使用整型量化系数和自动放大器（表示为 α），在保持类似准确性的同时缓解了问题。注意 sij 是每个权重组 gij 的比例因子，而 sai 是激活 X 的比例因子。

鉴于前面的讨论，提高细粒度推理的速度变得至关重要。图 3（b）显示，使用浮点量化系数会触发许多昂贵的类型转换。例如，一个典型的 4096×4096 大小的密集层，分为 128 组，会有 131072 个浮点量化系数，因此需要同样数量的 4 种类型转换操作。每个操作都需要额外的逐元素转换。

直观地，该文可以求助于整数量化系数来避免这种情况。然而，由于所有归一化的浮点量化系数都在（0, 1）范围内，直接将量化系数转换为整数肯定会造成巨大的量化误差。为了缓解这个问题，该文引入了一个整数放大器 α，称为自适应量化系数放大器，它可以根据可用的浮点量化系数轻松计算出来。该文的方法可以正式表述为：

其中 α 是自适应量化系数放大器，它可以调整量化后的值以减少量化误差。通过这种方式，该文能够在不进行昂贵的类型转换的情况下，保持量化操作的精度，从而提高推理速度。

这种方法的核心在于找到一种平衡，既能利用整数运算的速度优势，又能通过自适应放大器减少量化过程中的精度损失。通过精心设计的放大器，该文可以在不牺牲太多精度的情况下，显著提高细粒度量化模型的推理效率。

为了找到共同的放大器，该文使用启发式搜索算法，从开始放大所有组的最小量化系数，直到该文找到一个放大器，它确保放大后的量化系数大于 1，见下面代码。

scale_min = scales . min ()
n , tmp = 0 , scale_min
while tmp < 1:
  tmp = scale_min * (2** n )
  n +=1
scale_amplifier = 2**( n -1)

这里的启发式搜索算法是一种优化方法，用于在一组可能的放大值中找到合适的放大器 α。算法从（即 1）开始，逐步增加放大倍数，直到找到最小的，使得所有组的放大量化系数都大于 1。这样做的目的是为了确保量化后的量化系数不会由于直接转换为整数而产生下溢（即变得太小，接近或等于 0）。

这种方法的优点在于它简单且高效，能够快速找到一个合适的放大器，从而在不牺牲太多精度的情况下减少量化误差。通过这种方式，该文可以在保持量化操作的精度的同时，提高模型的推理速度。

理想情况下，该文可以使用上述启发式方法为每层找到最优的放大器。然而，基于图 4（a,b,c）中对 LLaMA-2-7B 模型的量化系数分析，该文发现放大量化系数所需的移位数主要落在 9 或 10。使用作为放大器时，与其浮点数版本相比较权重均方误差（Mean Squared Error, MSE）在到的范围内。

对于 13B 和 70B 模型，也有类似的观察结果。该文选择作为该文的默认放大器，以避免可能的溢出，后续的消融实验显示更大的放大器并没有明显的增益。

▲ 图4：（a）在第一层中放大（α = 210）的 LLaMA-2-7B 浮点比例因子的范围（其他层类似）映射到 16 位整数。大多数放大的比例因子可以在 8 位内表示。（b）每个线性层所需的位数移动数量以放大比例因子。（c）在不同放大器下整型量化系数与浮点比例因子之间的权重均方误差（Weight MSE）。

在实际应用中，尽管理论上可以为每个层找到最优的放大器，但在实践中，通过对特定模型的量化系数分析，可以确定一个适用于大多数情况的默认放大器。

实验

5.1 Common Sense QA 量化结果

见表 1，整数量化系数（IS）在 Common Sense QA 数据集上能够保持常见的大模型量化算法的精度，有些甚至有增益。

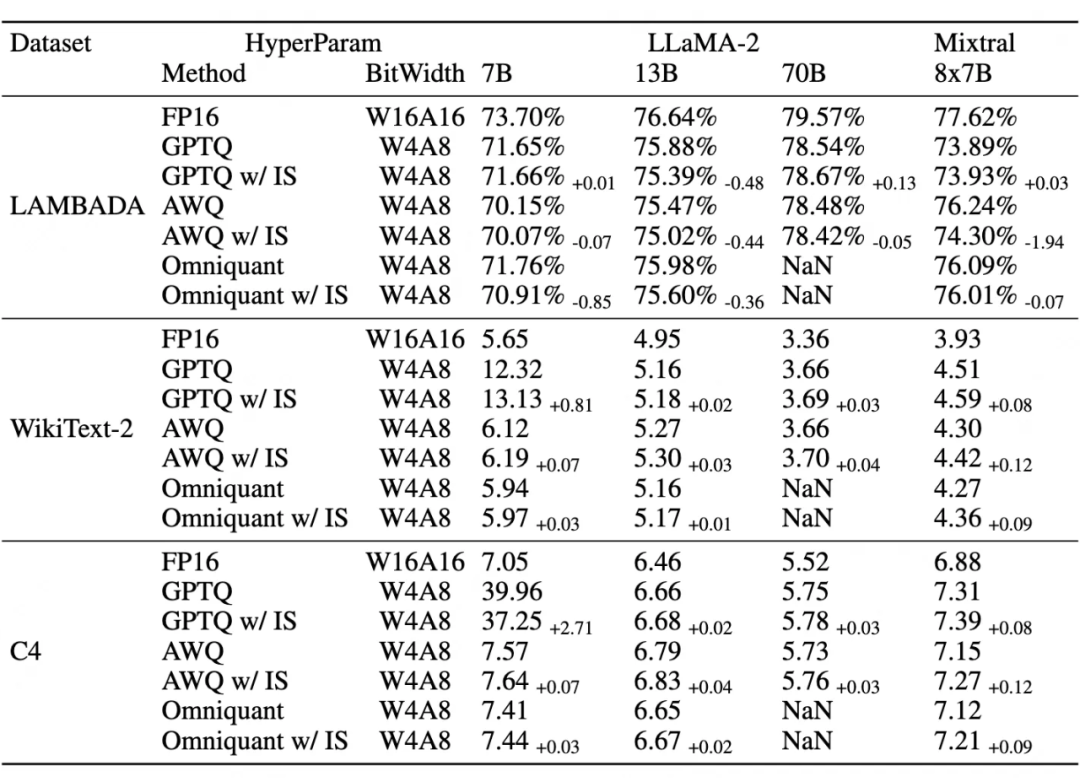
▲ 表1：在LAMBADA（准确性）、C4（困惑度）和 WikiText（困惑度）上与最先进量化方法的比较。对于所有测试的模型，该文将权重组大小设置为 128，并应用对称量化。使用放大器 1024 的整数量化系数（IS）。

5.2 Kernel 实现对比

图 5（a）展示了在不同带宽条件下 Kernel 实现对比。Marlin [13] 到目前为止提供了最先进的 W4A16 Kernel 实现。Odyssey 的 W4A8 方案受益于其 FastGEMM 的设计，并且在 FP16 上具有最佳的加速比。可以看出，细粒度的 W4A8 使用整型量化系数成为一种在 W4A16 和非细粒度 W4A8 之间的可行方案，以获得更好的准确性。

有趣的是，该文发现了一个“性能悬崖”（灰色区域），当从内存限制转变为计算限制场景时，加速比突然下降。这是由于理想的加速比从 4 倍突然下降到与 FP16 相比的 2 倍。

▲ 图5：（a）细粒度的 W4A8 核（K=4096, N=22016）使用整型量化系数（W4A8 整数量化系数）提升了其浮点比例因子对应模型（W4A8 浮点比例因子）的性能。灰色区域表示“性能悬崖”。（b）在不同批量大小下，Mixtral 8x7B 在 FP16 上的端到端速度提升。

图 6 展示了和最新 W4A8KV4 量化方案 QServe [27] 的 Kernel 性能对比。不论是细粒度，还是粗粒度的性能，该文的 Kernel 相对于 FP16 的加速比都要高于 QServe。尽管位宽相同，细粒度内核使用整数量化系数速度明显快于 QServe，最高可达 1.53 倍。

结果表明，主要差异在于他们采用的双重量化的内在复杂性 [51]，该方法首先将权重量化为 8 位，然后再量化为 4 位，第二步中保持了不对称性以抵消量化损失。这种不对称方案需要进行逐元素乘法和减法，这必须在成本较高的 CUDA 核心上完成。

▲ 图6：在特定参数设置下（K=4096, N=22016），同 QServe 的 W4A8 内核、FP16 内核的速度比较

5.3 Mixture-of-experts 量化加速

图 5（c）展示了将 W4A8 整型量化系数方案应用于 Mixtral 8×7B 时的端到端延迟，与 FP16和 W4A16 相比，最多获得了 1.55 倍和 1.3 倍的提升。证明对与 MoE 模型该方法也具有鲁棒性。

5.4 LLaMA-3 量化方案

LLaMA-3 与其前代相比，在较低位宽的量化上存在困难，这一点在文献 [17] 中得到了证实。为了解决这个问题，该文应用了 QuaRot [3]，并采用了细粒度范式。该文采用了每个 token 8 位的激活量化和每个通道 4 位的对称权重量化，组大小为 128。

此外，根据文献 [24] 的观察，该文对下投影层使用了细粒度的 W8A8。表 2 展示了该文 LLaMA-3 方案的结果，其中整型量化系数的性能超过了 GPTQ 的 W4A16（在 C4 的困惑度上降低了 1.16%）。

▲ 表2：LLaMA-3 整型量化系数方案

结论

该文介绍了一种即插即用的方案，称为整数量化系数（Integer Scale），它可以用来加速现有的细粒度量化方法。该文通过广泛的实验表明，整数量化系数不仅受益于细粒度带来的性能提升，而且很好地解决了内在的计算开销问题。它可以作为一种默认的免费午餐技术，与各种带宽的细粒度方法结合使用，以实现整体上具有竞争力的量化策略。

此外，相同的策略也可以应用于基于混合专家技术的 Mixtral 8×7B 和 LLaMA-3，解决了这些模型以前在较低位宽下量化精度下降明显的难题。

参考文献

[1] AI@Meta. Llama 3 model card. 2024. URL https://github.com/meta-llama/llama3/ blob/main/MODEL_CARD.md

[3] Saleh Ashkboos, Amirkeivan Mohtashami, Maximilian L Croci, Bo Li, Martin Jaggi, Dan Alistarh, Torsten Hoefler, and James Hensman. Quarot: Outlier-free 4-bit inference in rotated llms. arXiv preprint arXiv:2404.00456, 2024

[13] Elias Frantar and Dan Alistarh. Marlin: a fast 4-bit inference kernel for medium batchsizes. https://github.com/IST-DASLab/marlin, 2024

[14] Elias Frantar, Saleh Ashkboos, Torsten Hoefler, and Dan Alistarh. Gptq: Accurate post-training quantization for generative pre-trained transformers. arXiv preprint arXiv:2210.17323, 2022

[17] Wei Huang, Xudong Ma, Haotong Qin, Xingyu Zheng, Chengtao Lv, Hong Chen, Jie Luo, Xiaojuan Qi, Xianglong Liu, and Michele Magno. How good are low-bit quantized llama3 models? an empirical study. arXiv preprint arXiv:2404.14047, 2024

[18] Albert Q Jiang, Alexandre Sablayrolles, Antoine Roux, Arthur Mensch, Blanche Savary, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Emma Bou Hanna, Florian Bressand, et al. Mixtral of experts. arXiv preprint arXiv:2401.04088, 2024

[24] Qingyuan Li, Yifan Zhang, Liang Li, Peng Yao, Bo Zhang, Xiangxiang Chu, Yerui Sun, Li Du, and Yuchen Xie. Fptq: Fine-grained post-training quantization for large language models. arXiv preprint arXiv:2308.15987, 2023

[26] Ji Lin, Jiaming Tang, Haotian Tang, Shang Yang, Xingyu Dang, and Song Han. Awq: Activation- aware weight quantization for llm compression and acceleration, 2023

[27] Yujun Lin, Haotian Tang, Shang Yang, Zhekai Zhang, Guangxuan Xiao, Chuang Gan, and Song Han. Qserve: W4a8kv4 quantization and system co-design for efficient llm serving. arXiv preprint arXiv:2405.04532, 2024

[28] Zechun Liu, Barlas Oguz, Changsheng Zhao, Ernie Chang, Pierre Stock, Yashar Mehdad, Yangyang Shi, Raghuraman Krishnamoorthi, and Vikas Chandra. Llm-qat: Data-free quantiza- tion aware training for large language models, 2023.

[49] Zhewei Yao, Reza Yazdani Aminabadi, Minjia Zhang, Xiaoxia Wu, Conglong Li, and Yuxiong He. ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers. arXiv preprint arXiv:2206.01861, 2022

[51] Luoming Zhang, Wen Fei, Weijia Wu, Yefei He, Zhenyu Lou, and Hong Zhou. Dual grained quantization: Efficient fine-grained quantization for LLM, 2024

更多阅读